Definições
Definição: Sejam U e V espaços
vetoriais sobre um corpo K. Denotamos
o conjunto de todas as transformações lineares
de U em V. O conjuntos dos operadores lineares de U será
denotado por
.
Definição: Sejam . A Adição de F com G é uma aplicação, , dada por:
Propriedades da Adição: Para toda valem as seguintes propriedades:
(A1) Associativa: ;
(A2) Comutativa: ;
(A3) Existe um elemento neutro de ;
(A4) Para toda existe a transformação oposta tal que , onde é a transformação nula.
Veja as demonstrações AQUI.
Definição: Sejam e . A Multiplicação da transformação F por um escalar é uma aplicação , dada por:
Propriedades da Multiplicação por Escalar: Para toda e valem as seguintes propriedades:
(M1) Associativa: ;
(M2) ;
(M3) ;
(M4) ;
Veja as demonstrações AQUI.
Podemos concluir que , o conjunto de todas as transformações lineares de U em V, com as operações de Adição e Multiplicação por um escalar definidas, com suas respectivas propriedades, é um espaço vetorial.
Definição: Sejam U, V e W espaços vetoriais sobre um corpo K. Sejam e transformações lineares. A Composição das transformações F e G é uma aplicação, denotada por , dada por:
As operações de adição, multiplicação por escalar e composição de transformações lineares são transformações lineares. Demonstração: AQUI.
Definição: No espaço vetorial podemos definir a operação de Potenciação para expoentes naturais da seguinte forma:
Dizemos que F é um operador idempotente ou projeção se , F é um operador auto-reflexivo se (transformação identidade) e F é um operador nilpotente se (transformação nula), para algum .
Voltar ao Topo.
Definição: Sejam . A Adição de F com G é uma aplicação, , dada por:
Propriedades da Adição: Para toda valem as seguintes propriedades:
(A1) Associativa: ;
(A2) Comutativa: ;
(A3) Existe um elemento neutro de ;
(A4) Para toda existe a transformação oposta tal que , onde é a transformação nula.
Veja as demonstrações AQUI.
Definição: Sejam e . A Multiplicação da transformação F por um escalar é uma aplicação , dada por:
Propriedades da Multiplicação por Escalar: Para toda e valem as seguintes propriedades:
(M1) Associativa: ;
(M2) ;
(M3) ;
(M4) ;
Veja as demonstrações AQUI.
Podemos concluir que , o conjunto de todas as transformações lineares de U em V, com as operações de Adição e Multiplicação por um escalar definidas, com suas respectivas propriedades, é um espaço vetorial.
Definição: Sejam U, V e W espaços vetoriais sobre um corpo K. Sejam e transformações lineares. A Composição das transformações F e G é uma aplicação, denotada por , dada por:
As operações de adição, multiplicação por escalar e composição de transformações lineares são transformações lineares. Demonstração: AQUI.
Definição: No espaço vetorial podemos definir a operação de Potenciação para expoentes naturais da seguinte forma:
Dizemos que F é um operador idempotente ou projeção se , F é um operador auto-reflexivo se (transformação identidade) e F é um operador nilpotente se (transformação nula), para algum .
Voltar ao Topo.
Exemplos
Exemplo 1: Considere F, G e H
operadores lineares em ,
dados por: ,
,
.
Determinar: F+G, F+3G-H, ,
,
,
,
,
e .
Neste caso, todas as aplicações estão bem definidas, pois F, G e H são ambos operadores lineares de . Assim, temos:
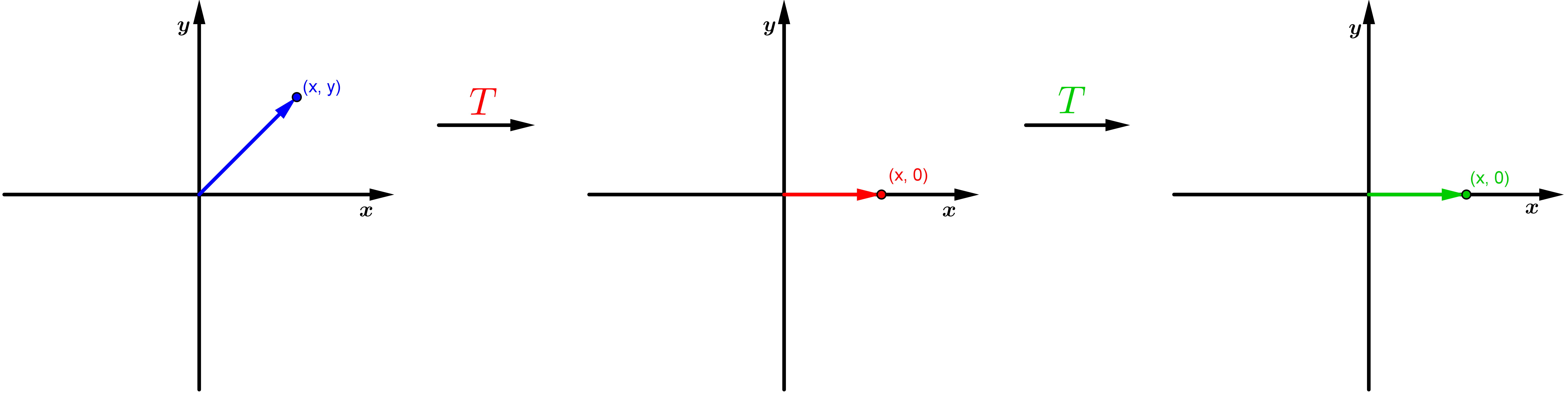
Exemplo 2: O operador linear de projeção sobre o eixo x:
é um operador idempotente.
De fato, temos que:
Assim, e o operador é idempotente. Observe que com a transformação T, cada elemento (x,y) é projetado no eixo x e, uma vez no eixo x, sua projeção coincide com ele mesmo.
é um operador auto-reflexivo.
De fato, temos que:
Assim, e o operador é auto-reflexivo. Observe que com a transformação T, cada elemento (x,y) é refletido com relação ao eixo x e, uma vez refletido, sua reflexão volta a ser o próprio elemento (x,y).
Neste caso, todas as aplicações estão bem definidas, pois F, G e H são ambos operadores lineares de . Assim, temos:
- ;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
- .
Exemplo 2: O operador linear de projeção sobre o eixo x:
é um operador idempotente.
De fato, temos que:
Assim, e o operador é idempotente. Observe que com a transformação T, cada elemento (x,y) é projetado no eixo x e, uma vez no eixo x, sua projeção coincide com ele mesmo.

O operador
linear T é um operador idempotente.
Exemplo 3:
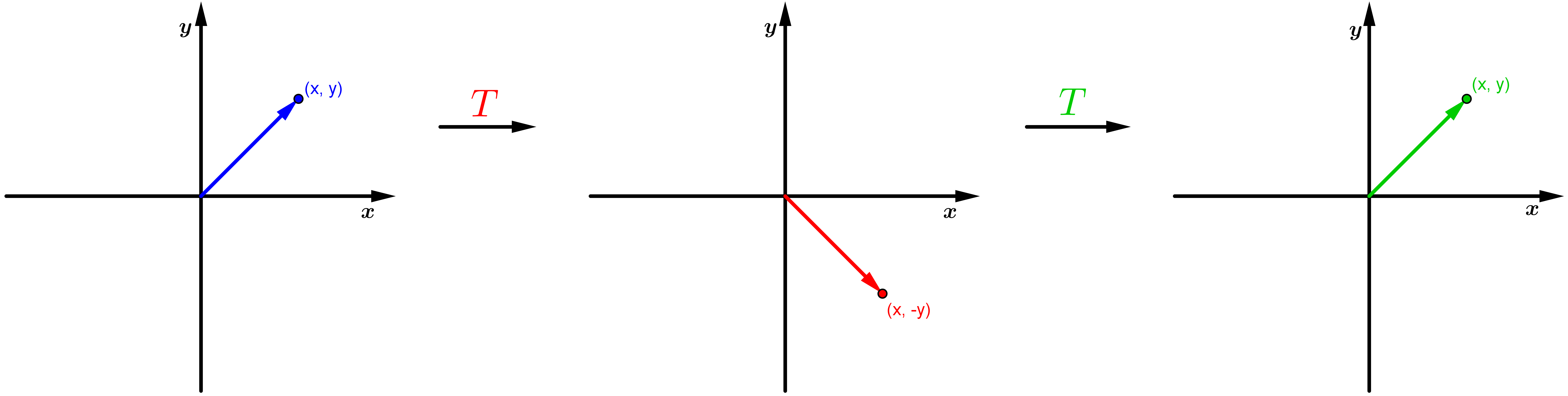
O operador linear de reflexão em torno do eixo x:é um operador auto-reflexivo.
De fato, temos que:
Assim, e o operador é auto-reflexivo. Observe que com a transformação T, cada elemento (x,y) é refletido com relação ao eixo x e, uma vez refletido, sua reflexão volta a ser o próprio elemento (x,y).
