Subespaços Vetoriais

Definição

   Seja $V$ um Espaço Vetorial sobre o corpo $K$. Um Subespaço Vetorial $S$ de $V$ é um subconjunto de $V$, que por si só também é um espaço vetorial, definido sobre o mesmo corpo que $V$ e com as mesmas operações definidas em $V$.

    Teorema: Um subconjunto não vazio $S$ de um espaço vetorial $V$ é um subespaço vetorial de $V$ se, e somente se, satisfaz as condições:

    (i) O elemento neutro $e$ de $V$ está em $S$;
    (ii) A operação de Adição definida em $V$ é fechada em $S$, ou seja, $u+v \in S$, $\forall u,v \in S$;
    (iii) A operação de Multiplicação por escalar de $V$ é fechada em $S$, ou seja, $\alpha u \in S$, $\forall u \in S$ e $\forall \alpha \in K$.

    Demonstração: AQUI.

Exemplos

    Exemplo 1: $U = \left\lbrace u \in R^2 \mid u = \alpha (1,1), \forall \alpha \in R \right\rbrace$  é subespaço de $R^2$. Ou seja, qualquer reta passando pela origem é um subespaço de $R^2$.

Vamos verificar que valem as condições (i), (ii) e (iii) para $U$:

    (i) O elemento neutro do $R^2$ é a origem $(0,0)$. Para $\alpha = 0$, $\alpha (1,1) = 0(1,1) = (0,0)$, logo, o elemento neutro pertence a $U$;
    (ii) Tome $u,v \in U$ e $\alpha_1, \alpha_2 \in R$. Temos, $u+v = \alpha_1 (1,1) + \alpha_2 (1,1) = (\alpha_1 + \alpha_2)(1,1)$. Assim, $u+v \in U$, uma vez que $\alpha_1+\alpha_2 \in R$;
    (iii) Tome $u \in U$ e $\alpha, \beta \in R$, temos $\beta u = \beta (\alpha (1,1)) = \beta \alpha (1,1)$. Assim, $\beta u \in U$, uma vez que $\beta\alpha \in R$.

Logo, $U$ é subespaço de $R^2$.

    Exemplo 2: Qualquer reta que não passe pela origem NÃO é subespaço de $R^2$.

De fato, se a reta não passa pela origem, ela não contem o elemento neutro $(0,0)$ do $R^2$. Logo não pode ser subespaço vetorial.

    A figura a seguir ilustra os exemplos 1 e 2:

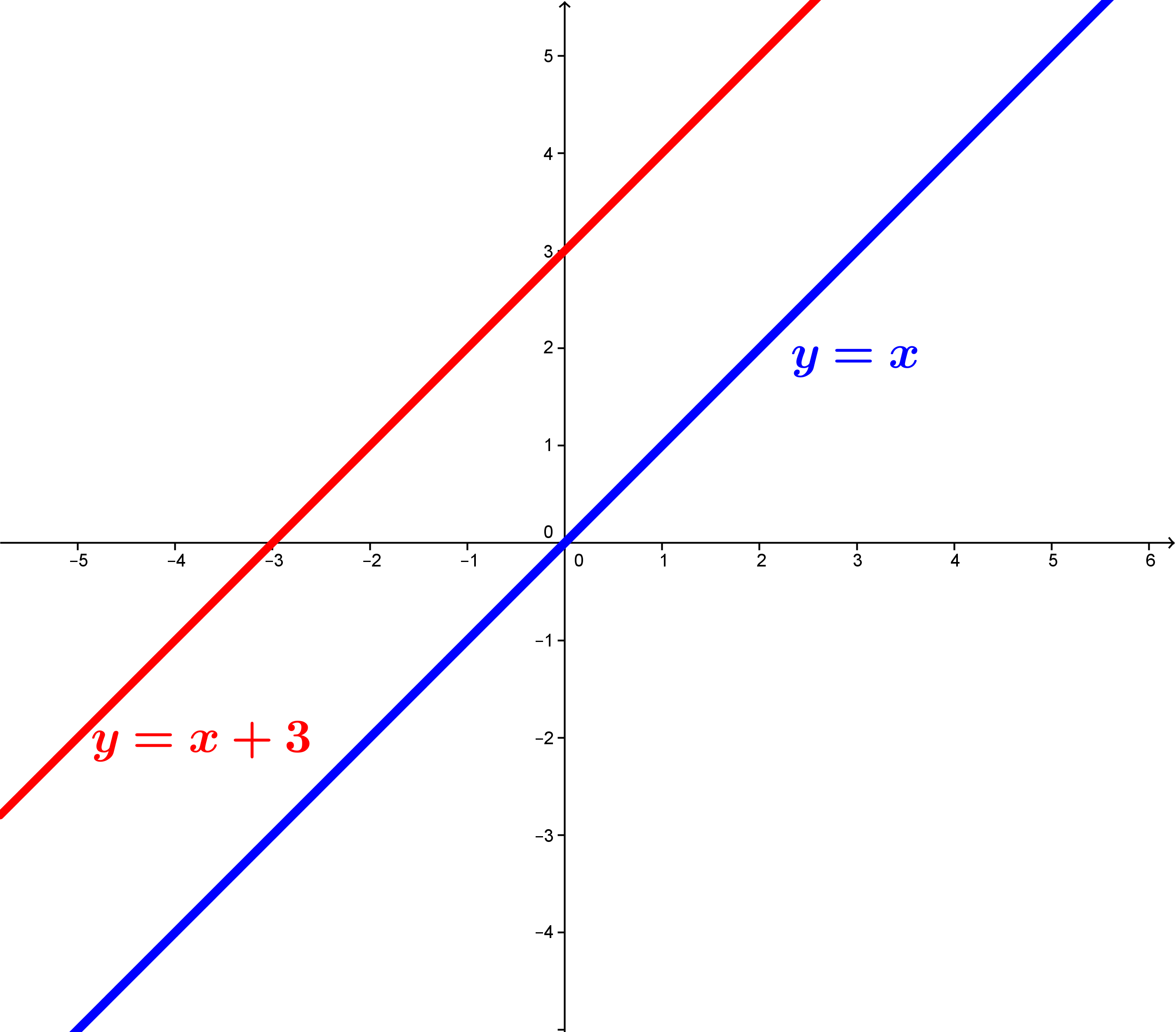
                                                          A reta $y = x+3$ não é um subespaço de $R^2$. enquanto que a reta $y = x$ é um subespaço de $R^2$.

    Exemplo 3: $U$$S=\left\lbrace (x,y) \in R^2 \mid x\geq 0, y\geq 0 \right\rbrace$ NÃO é um subespaço vetorial do $R^2$. Geometricamente, $U$ é o primeiro quadrante dos eixos coordenados.

De fato, não vale a propriedade (iii) para $U$, pois basta tomar $\alpha$ um número negativo. Assim, as coordenadas de $\alpha u$ não serão positivas, para um $u \in U$.

$U$ não é um subespaço de $R^2$.

    Veja estes e mais exemplos AQUI.

    Voltar ao Topo.