Soma de Subespaços

Definições

    Definição: Sejam U e W subespaços vetoriais de um espaço vetorial V. A Soma dos subespaços U e W é dada por:

$$U+W = \left\lbrace v \in V \mid v = u+w ; \, u \in U \,\,\mbox{e}\,\, w \in W \right\rbrace$$
Ou seja, são todos os elementos de V que são soma de um elemento de U com um elemento de W.

    Teorema: A Soma dos subespaços vetoriais U e W de V é também um subespaço vetorial de V.
    Demonstração: AQUI.

    Definição: Sejam U e W subespaços vetoriais de um espaço vetorial V, quando $U \cap W = \left\lbrace e \right\rbrace$, onde $e$ é o elemento neutro de V. Dizemos que U+W é Soma Direta dos subespaços U e W, que denotamos por $U \oplus W$.

Resultados Teóricos

    Proposição: Considerando os subespaços $U = [S_1]$ e $W = [S_2]$, ou seja, U é gerado pelos elementos do conjunto $S_1$ e W é gerado pelos elementos do conjunto $S_2,$ temos que $U+W = [S_1 \cup S_2]$, ou seja, a Soma dos subespaços U e W é gerada pela união dos conjuntos $S_1$ e $S_2$.
   
    Proposição: Sejam U e V subespaços vetoriais de um espaço vetorial V. Então, $V = U\oplus W$ se, e somente se, cada elemento $v \in V$ pode ser escrito de forma única pela combinação $v = u + w$, com $u \in U$ e $w \in W$.
   
    Veja as demonstrações: AQUI.

    Voltar ao Topo.

Exemplos

    Exemplo 1: O espaço vetorial $R^2$ é soma direta dos subespaços $U = \left\lbrace (x,y) \in R^2 \mid y=0\right\rbrace$ e $W\left\lbrace (x,y) \in R^2 \mid x=0\right\rbrace$. Ou seja, $R^2 = U \oplus W$.

Temos que um elemento de U é da forma $(x,y)$ com $y=0$, ou seja, $(x,0) = x(1,0)$, para $x \in R$. Assim, o conjunto U é gerado pelo elemento $(1,0)$, isto é, $U=[(1,0)]$.
De mesmo modo, um elemento de W é da forma $(0,y) = y(0,1)$, para $y \in R$. Assim, o conjunto W é gerado pelo elemento $(0,1)$, isto é $W = [(0,1)]$.
Logo, temos que a intersecção entre U e W é o elemento neutro de $R^2$, ou seja, $U \cap W = \left\lbrace (0,0) \right\rbrace$

Além disso, $U+W = [(1,0),(0,1)]$.
Mas, o conjunto  $\left\lbrace (1,0),(0,1)\right\rbrace$  gera todo o $R^2$, pois qualquer elemento $(x,y) \in R^2$ pode ser escrito como a combinação linear $(x,y) = x(1,0) + y(0,1)$. Assim, temos que $U+W = R^2$.
E como $U \cap W = \left\lbrace (0,0)\right\rbrace$ , temos:
$$R^2 = U \oplus W$$
De fato, qualquer elemento $(x,y) \in R^2$ pode ser escrito como combinação de um elemento de U, da forma $(x,0)$ com um de W, da forma $(0,y)$ e o único elemento que pertence a U e a W ao mesmo tempo é a origem $(0,0)$.

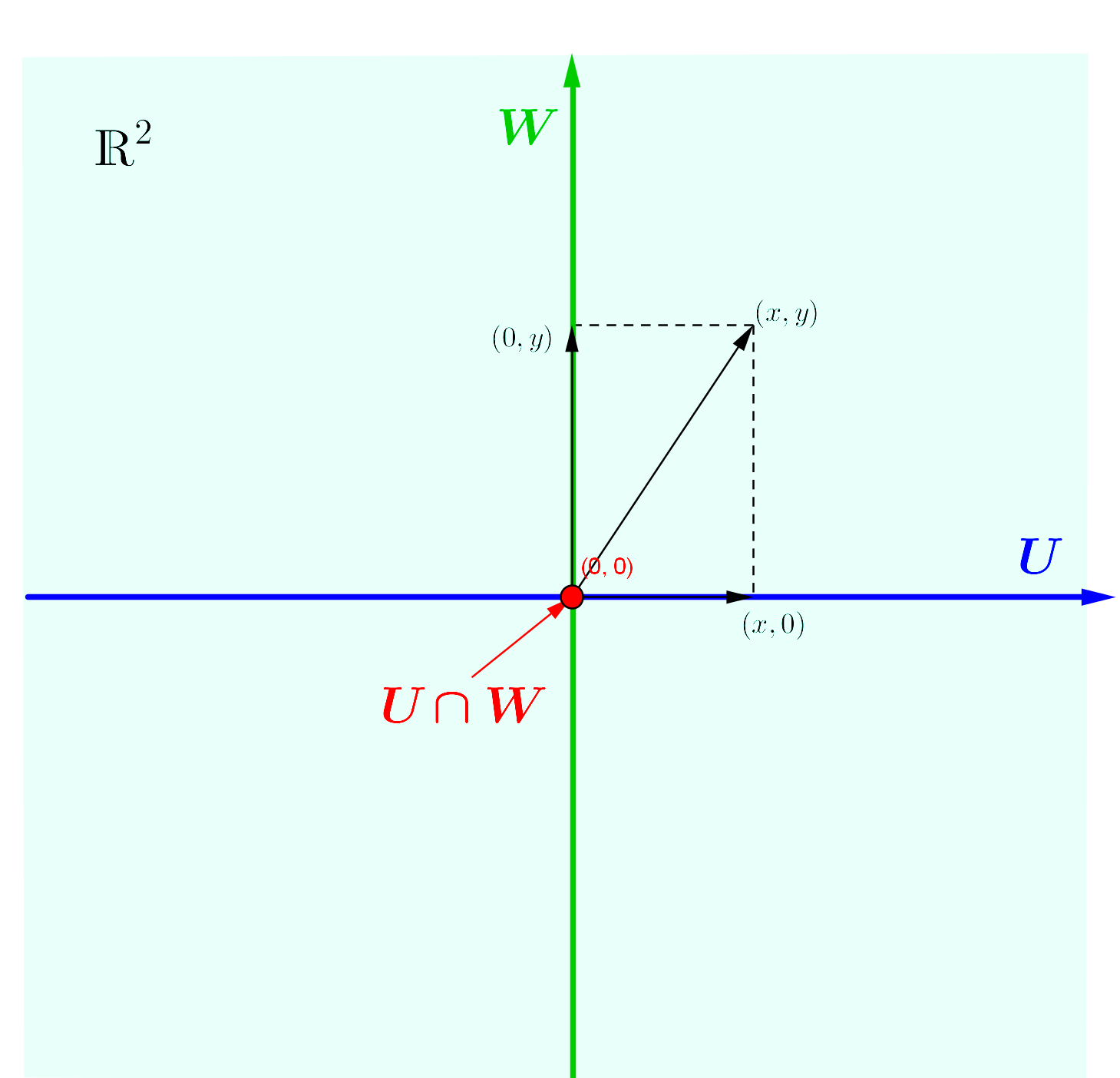
    Exemplo 2: Sejam $U = \left\lbrace A \in M_n(R) \mid A^t = A \right\rbrace$ e $W = \left\lbrace B \in M_n(R) \mid B^t = -B \right\rbrace$ subespaços vetoriais de $M_n(R)$, das matrizes $n \times n$. Temos que $M_n(R) = U \oplus W$.

O exemplo pode ser visto da seguinte forma: Toda matriz $n \times n$ pode ser escrita como combinação de uma matriz simétrica com uma antissimétrica.
Vamos determinar de forma única duas matrizes, A e B com $A \in U$ simétrica e $B \in W$ antissimétrica, tais que M = A + B, com M uma matriz qualquer:

Temos que $A^t = A$ e $B^t = -B$, assim:
$$\left\lbrace \begin{array}{l} M = A + B \\ M^t = A^t + B^t = A - B \end{array}\right.$$
Somando as duas equações obtemos: $M + M^t = 2A \Rightarrow A = \frac{M+M^t}{2}$.
Agora, subtraindo as duas equações do sistema, temos: $M - M^t = 2B \Rightarrow B = \frac{M-M^t}{2}$.

Dessa forma, determinamos de forma única duas matrizes A e B, com $A \in U$ e $B \in W$, de modo que M = A + B, para $M \in M_n(R)$.
Assim, temos que $M_n(R) = U \oplus W$.

    Veja estes e mais exemplos AQUI.

    Voltar ao Topo.