Classificação de Cônicas

    Definição: Uma cônica em $R^2$ é um conjunto de pontos cujas coordenadas, em relação à base canônica, satisfazem a equação geral:

$$Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0$$
onde A ou B ou C é diferente de zero. $Ax^2 + Bxy + Cy^2$ é a forma quadrática da cônica, $Dx + Ey$ a forma linear e F é o termo constante.

   Uma cônica pode ser classificada como: circunferência, elipse, parábola ou hipérbole. Dada uma equação na forma geral, estamos interessados em classificar qual é o tipo de cônica de modo a facilitar seu estudo e representação gráfica.

    Da Geometria Analítica sabemos que esses tipos de cônicas possuem equações na forma reduzida dadas por:

$$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$
onde $(\pm a, 0)$ e $(0, \pm b)$ são os vértices da elipse. Observe que uma circunferência é uma elipse onde $a = b = r$, que é o raio da circunferência $(x^2+y^2 = r^2)$.

$$y^2 = 4px \;\;\;\; ou \;\;\;\; y^2 = -4px \;\;\;\; ou \;\;\;\; x^2 = 4py \;\;\;\; ou \;\;\;\; x^2 = -4py$$
onde a primeira equação representa uma parábola com foco $(p, 0)$, a segunda com foco $(-p,0)$, a terceira com foco $(0,p)$, e a quarta uma parábola com foco $(0,-p)$.

$$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\;\;\;\;\;\; ou \;\;\;\;\;\; -\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$
onde a primeira equação representa uma hipérbole com focos no eixo $x$ e vértices $(\pm a, 0)$, e a segunda uma hipérbole com focos no eixo $y$ e vértices $(0, \pm b)$.

    As equações das cônicas representadas acima estão na forma reduzida, onde temos B = 0, se $A \neq 0$, D = 0 e se $C \neq 0$, E = 0. Veremos que é possível, através de uma mudança de referencial conveniente, levar a equação geral de uma cônica até a forma reduzida, a fim de facilitar a sua classificação e estudo. Para isso utilizaremos conceitos de autovalores e autovetores, e a diagonalização de matrizes.

    Voltar ao Topo.

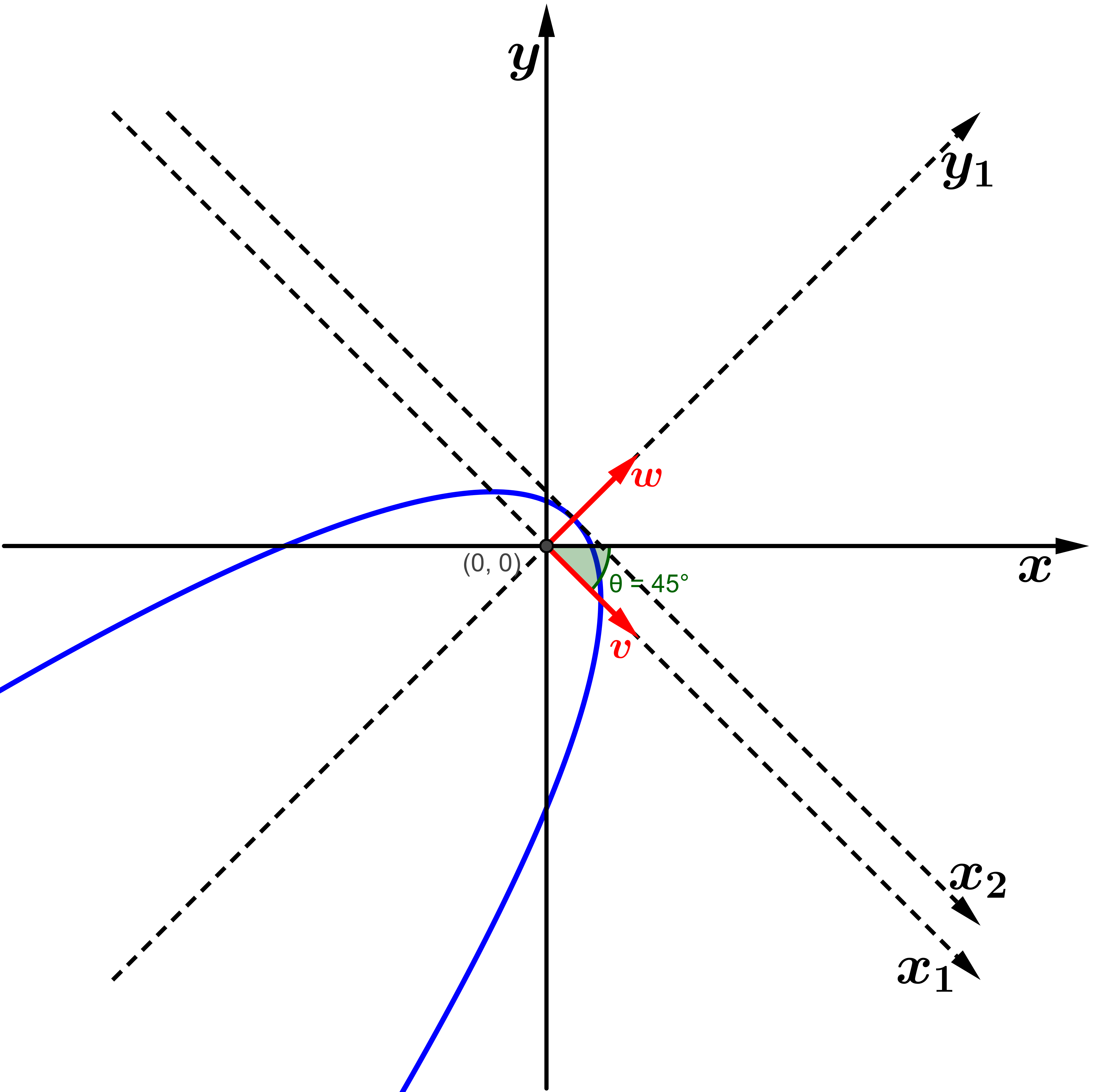
    Exemplo 1: Considere a equação da cônica: $x^2 + y^2 - 6x - 4y + 9 = 0$, em coordenadas canônicas do $R^2$. Esta equação não está na forma reduzida, e não sabemos definir qual é o tipo de cônica. Mas, podemos escrevê-la como:

$$x^2 + y^2 - 6x - 4y + 9 = x^2 - 6x + (9 - 9) + y^2 - 4y + (4 - 4) + 9 = 0 \Rightarrow$$
$$\Rightarrow (x - 3)^2 + (y - 2)^2 - 9 - 4 + 9 = 0 \Rightarrow (x - 3)^2 + (y - 2)^2 = 4$$
Fazendo uma mudança de referencial da forma: $x_1 = x - 3$ e $y_1 = y-2$, obtemos:

$$x_1^2 + y_1^2 = 4$$
E assim, podemos identificar a cônica como sendo uma circunferência de raio 2, centrada no ponto $(3,2)$, com relação ao referencial canônico $xy$.

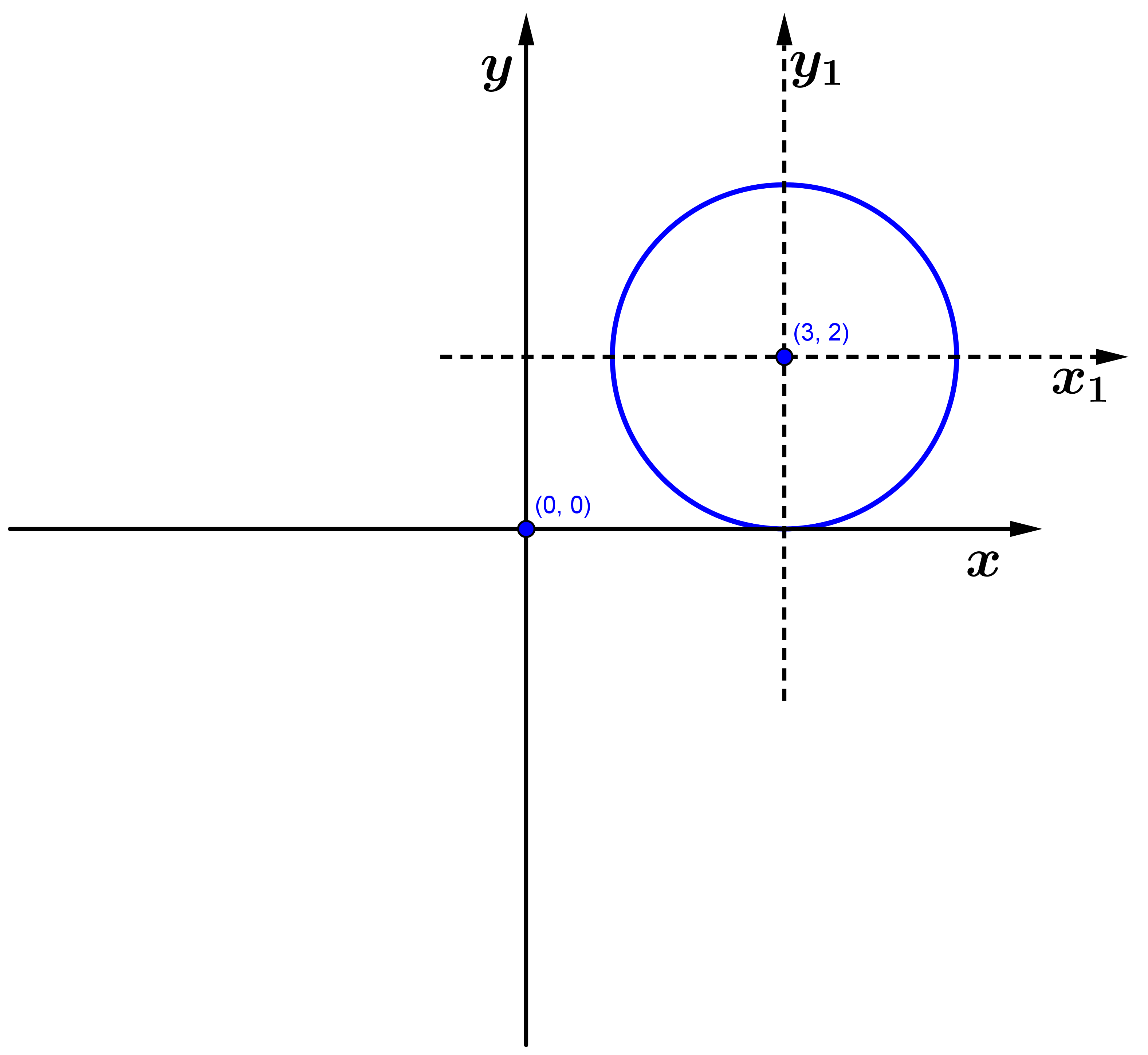
A circunferência $x^2 + y^2 - 6x - 4y + 9 = 0$ no referencial $xy$ é a mesma circunferência $x_1^2 + y_1^2 = 4$ no referencial $x_1y_1$.

    Esse é um exemplo simples no qual a equação da cônica não possuía o termo misto $Bxy$, ou seja, B = 0. Neste caso, a cônica está na forma reduzida em um referencial transladado em relação ao referencial canônico $xy$ do $R^2$. Caso a equação da cônica possua o termo misto, ou seja, $B \neq 0$, a cônica estará também rotacionada com relação ao referencial canônico do $R^2$. Para classificar a cônica, precisamos inicialmente eliminar o termo misto. Faremos isso utilizando a diagonalização de matrizes.

---

    Considere a equação geral da cônica em coordenadas canônicas do $R^2$, dada por:

$$Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0$$
Para obter a cônica na forma reduzida em um outro referencial do $R^2$, procedemos da seguinte forma:

Passo 1: Escrevemos a equação da cônica na forma matricial:

$$\left[ \begin{array}{cc} x & y \end{array}\right] \; \left[ \begin{array}{cc} A & \frac{B}{2} \\ \frac{B}{2} & C \end{array}\right] \;\left[ \begin{array}{c} x \\ y \end{array}\right] + \left[ \begin{array}{cc} D & E \end{array}\right] \;\left[ \begin{array}{c} x \\ y \end{array}\right] + F = 0$$
Observe que se a matriz
$$M = \left[ \begin{array}{cc} A & \frac{B}{2} \\ \frac{B}{2} & C \end{array}\right]$$
for diagonal, teremos que B = 0 e assim eliminamos o termo misto $Bxy$ da equação da cônica. Observe que a matriz M é sempre simétrica, o que implica que ela é sempre diagonalizável, por isso podemos utilizar a diagonalização para eliminar o termo misto da equação.

Passo 2: Diagonalizamos a matriz M para eliminar o termo misto, para isso precisamos encontrar os autovalores $\lambda_1$ e $\lambda_2$ e os autovetores  ortonormais $v$ e $w$ de M. Faremos então uma mudança de referencial, de modo a obter a equação da cônica com coordenadas em relação a um referencial cujos eixos são determinados pelos autovetores ortonormais da matriz M, ou geometricamente, um ponto $P = (x,y)$ representado no sistema canônico de base $\left\lbrace (1,0), (0,1)\right\rbrace$ será representado no sistema de base $\left\lbrace v, w \right\rbrace$, onde $v$ e $w$ são os autovetores ortonormais da matriz M, e serão os vetores diretores dos eixos da cônica. De acordo com o que é estudado em ortogonalização de Gram-Schmidt, sabemos que toda base pode ser ortonormalizada. Logo, se temos uma base formada por autovetores de uma matriz, esta base pode ser ortonormalizada.

Sabemos que a matriz M pode ser diagonalizada considerando como matriz diagonalizante U, a matriz cujas colunas são autovetores linearmente independentes de M e como matriz diagonal D, a matriz cujas entradas da diagonal são os autovalores de M:

$$U = \left[ \begin{array}{cc} v & w \end{array}\right] \;\;\;\;\;\; e \;\;\;\;\;\; D = \left[ \begin{array}{cc} \lambda_1 & 0 \\ 0 & \lambda_2 \end{array}\right]$$ 
Dessa forma, temos $M = UDU^{-1} \Rightarrow D = U^{-1}MU$.

Passo 3: Fazemos uma mudança de referencial. Considere a base canônica $\left\lbrace (1,0), (0,1)\right\rbrace$ e a base $\left\lbrace v, w \right\rbrace$. Observe que a matriz de mudança da base canônica para a nova base de autovetores é exatamente a matriz U. Além disso, a existência do termo misto indica que a cônica está rotacionada em relação aos eixos canônicos, e então, U é a matriz de rotação, isto é, a matriz U é sempre da forma:

$$U = \left[ \begin{array}{rr} cos(\theta) & sen(\theta) \\ -sen(\theta) & cos(\theta) \end{array}\right]$$
onde $\theta$ é o ângulo de rotação. Observe que $U U^t = U^t U = I_2$, uma vez que U é formado por vetores de uma base ortonormal, ou seja, $U^{-1} = U^t$. Assim, temos $D = U^{-1}MU = U^tMU$.

Um ponto $(x,y)$ no referencial canônico pode ser representado no novo referencial $x_1y_1$ da forma:

$$\left[ \begin{array}{c} x \\ y \end{array}\right] = U \; \left[ \begin{array}{c} x_1 \\ y_1 \end{array}\right] \Rightarrow \left[ \begin{array}{c} x_1 \\ y_1 \end{array}\right] = U^{-1} \; \left[ \begin{array}{c} x \\ y \end{array}\right]$$
Assim, a forma quadrática da cônica fica:

$$\left[ \begin{array}{cc} x & y \end{array}\right] \; \left[ \begin{array}{cc} A & \frac{B}{2} \\ \frac{B}{2} & C \end{array}\right] \; \left[ \begin{array}{c} x \\ y \end{array}\right] = \left[ \begin{array}{cc} x_1 & y_1 \end{array}\right] \; U^T \; \left[ \begin{array}{cc} A & \frac{B}{2} \\ \frac{B}{2} & C \end{array}\right] \; U \; \left[ \begin{array}{c} x_1 \\ y_1 \end{array}\right] = \left[ \begin{array}{cc} x_1 & y_1 \end{array}\right] \; \left[ \begin{array}{cc} \lambda_1 & 0 \\ 0 & \lambda_2 \end{array}\right] \; \left[ \begin{array}{c} x_1 \\ y_1 \end{array}\right]$$
E a forma linear se reduz a:

$$\left[ \begin{array}{cc} D & E \end{array}\right] \; \left[ \begin{array}{c} x \\ y \end{array}\right] = \left[ \begin{array}{cc} D & E \end{array}\right] \; U \; \left[ \begin{array}{c} x_1 \\ y_1 \end{array}\right]$$
Substituíndo na equação geral da cônica, obtemos sua equação na nova base de autovetores $\left\lbrace v, w\right\rbrace$:

$$\left[ \begin{array}{cc} x_1 & y_1 \end{array}\right] \; \left[ \begin{array}{cc} \lambda_1 & 0 \\ 0 & \lambda_2 \end{array}\right] \; \left[ \begin{array}{c} x_1 \\ y_1 \end{array}\right] + \left[ \begin{array}{cc} D & E \end{array}\right] \; U \; \left[ \begin{array}{c} x_1 \\ y_1 \end{array}\right] + F = 0$$
Nesta nova equação o termo misto não aparece e a classificação da cônica se torna mais simples.

Passo 4: Se a nova equação da cônica possuir ambos os termos, quadrático e linear, em $x_1$ ou em $y_1$, completamos o quadrado para cada um deles, a fim de juntar esses termos em um único termo com $x_1$ e um termo com $y_1$. Por fim, realizamos uma nova mudança de referencial conveniente, obtendo a equação da cônica na forma reduzida no novo referencial $x_2y_2$. E logo, podemos classificá-la e representá-la graficamente.

    Voltar ao Topo.

---

    Exemplo 2: Considere a equação geral da cônica:

$$x^2+y^2-2xy+4x+4y-4=0$$
Escrevendo esta equação na forma matricial, temos:

$$\left[ \begin{array}{cc} x & y \end{array}\right] \; \left[ \begin{array}{rr} 1 & -1 \\ -1 & 1 \end{array}\right] \; \left[ \begin{array}{c} x \\ y \end{array}\right] + \left[ \begin{array}{cc} 4 & 4 \end{array}\right] \; \left[ \begin{array}{c} x \\ y \end{array}\right] - 4 = 0$$
Vamos diagonalizar a matriz
$$M = \left[ \begin{array}{rr} 1 & -1 \\ -1 & 1 \end{array}\right]$$para eliminar o termo misto da equação. Para isso, encontramos os autovalores e autovetores de M. O polinômio característico de M é:

$$p(\lambda) = det(M - \lambda I_2) = \left| \begin{array}{cc} 1-\lambda& -1 \\ -1 & 1-\lambda \end{array}\right| = (1-\lambda)^2 -1 = \lambda^2 -2\lambda$$
As raízes de $p(\lambda)$ são:

$$p(\lambda) = 0 \Leftrightarrow \lambda^2 -2\lambda = 0 \Leftrightarrow \lambda(\lambda - 2) = 0 \Leftrightarrow \lambda = 2 \;\; ou \;\; \lambda = 0$$
Portanto, $\lambda_1 = 2$ e $\lambda_2 = 0$ são os autovalores de M. Para $\lambda_1 = 2$, temos que:

$$Mv = \lambda_1 v \Leftrightarrow \left[ \begin{array}{rr} 1 & -1 \\ -1 & 1 \end{array}\right] \; \left[ \begin{array}{c} v_1 \\ v_2 \end{array}\right] = \lambda_1 \left[ \begin{array}{c} v_1 \\ v_2 \end{array}\right] \Leftrightarrow \left[ \begin{array}{r} v_1-v_2 \\ -v_1+v_2 \end{array}\right] = \left[ \begin{array}{c} 2v_1 \\ 2v_2 \end{array}\right] \Leftrightarrow$$ 
$$\Leftrightarrow \left\lbrace \begin{array}{r} v_1-v_2 = 2v_1\\ -v_1+v_2 = 2v_2 \end{array} \right. \Leftrightarrow v_2 = -v_1$$
Assim, os autovetores de M associados ao autovalor $\lambda_1$ são da forma:

$$v = v_1 \; \left[ \begin{array}{r} 1 \\ -1 \end{array}\right]$$Um autovetor normalizado é:

$$v = \left[ \begin{array}{r} \frac{\sqrt{2}}{2} \\ -\frac{\sqrt{2}}{2} \end{array}\right]$$
Para o autovalor $\lambda_2 = 0$, temos que:

$$Mv = \lambda_1 v \Leftrightarrow \left[ \begin{array}{rr} 1 & -1 \\ -1 & 1 \end{array}\right] \; \left[ \begin{array}{c} w_1 \\ w_2 \end{array}\right] = \lambda_2 \;\left[ \begin{array}{c} w_1 \\ w_2 \end{array}\right] \Leftrightarrow \left[ \begin{array}{r} w_1-w_2 \\ -w_1+w_2 \end{array}\right] = \left[ \begin{array}{c} 0 \\ 0 \end{array}\right] \Leftrightarrow$$
$$\Leftrightarrow \left\lbrace \begin{array}{r} w_1-w_2 = 0\\ -w_1+w_2 = 0 \end{array} \right. \Leftrightarrow w_2 = w_1$$
Assim, os autovetores de M associados ao autovalor $\lambda_2 = 0$ são da forma:

$$w = w_1 \; \left[ \begin{array}{c} 1 \\ 1 \end{array}\right]$$E um autovetor normalizado é:

$$w = \left[ \begin{array}{c} \frac{\sqrt{2}}{2}\\ \frac{\sqrt{2}}{2} \end{array}\right]$$
Portanto, a matriz M pode ser diagonalizada, com U a matriz diagonalizante e D a matriz diagonal, dadas por:

$$U = \left[ \begin{array}{rr} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\\ -\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{array}\right] \;\;\;\;\;\; e \;\;\;\;\;\; D = \left[ \begin{array}{rr} 2 & 0\\ 0 & 0 \end{array}\right]$$
Dessa forma, temos que $M = UDU^{-1} \Rightarrow D = U^{-1}MU = U^tMU$. Os autovetores $v$ e $w$ são vetores diretores dos eixos da cônica. Fazemos então uma mudança de coordenadas da base canônica do $R^2$ para a base $\left\lbrace v, w\right\rbrace$ . Observe que U é a matriz de mudança de base, e portanto é a matriz de rotação do novo referencial. Assim, temos:

$$\left\lbrace \begin{array}{c} \sin \theta = \frac{\sqrt{2}}{2} \\ \cos \theta = \frac{\sqrt{2}}{2} \end{array}\right. \Rightarrow \theta = \frac{\pi}{4}$$
Isto é, a cônica está rotacionada de um ângulo $\theta = \frac{\pi}{4} = 45^o$, no sentido horário, com relação aos eixos canônicos.
Como U é a matriz de mudança da base canônica para a base $\left\lbrace v, w\right\rbrace$, um elemento com coordenada $(x_1,y_1)$ na nova base é da forma:

$$\left[ \begin{array}{c} x \\ y \end{array}\right] = U \;\left[ \begin{array}{c} x_1 \\ y_1 \end{array}\right]$$
Portanto, a forma quadrática da equação da cônica se torna:

$$\left[ \begin{array}{cc} x & y \end{array}\right] \; \left[ \begin{array}{rr} 1 & -1 \\ -1 & 1 \end{array}\right] \; \left[ \begin{array}{c} x \\ y \end{array}\right] = \left[ \begin{array}{cc} x_1 & y_1 \end{array}\right] \; U^t \; \left[ \begin{array}{rr} 1 & -1 \\ -1 & 1 \end{array}\right] \; U \; \left[ \begin{array}{c} x_1\\ y_1 \end{array}\right] =$$
$$= \left[ \begin{array}{cc} x_1 & y_1 \end{array}\right] \; \left[ \begin{array}{rr} 2 & 0 \\ 0 & 0 \end{array}\right] \; \left[ \begin{array}{c} x_1\\ y_1 \end{array}\right] = 2x_1^2$$
E a forma linear se torna:

$$\left[ \begin{array}{cc} 4 & 4 \end{array}\right] \; \left[ \begin{array}{c} x \\ y \end{array}\right] = \left[ \begin{array}{cc} 4 & 4 \end{array}\right] \; \left[ \begin{array}{rr} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\\ -\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{array}\right] \; \left[ \begin{array}{c} x_1 \\ y_1 \end{array}\right] = \left[ \begin{array}{cc} 4 & 4 \end{array}\right] \; \left[ \begin{array}{rr} \frac{\sqrt{2}}{2}x_1 + \frac{\sqrt{2}}{2}y_1\\ -\frac{\sqrt{2}}{2}x_1 + \frac{\sqrt{2}}{2}y_1 \end{array}\right] =$$
$$= 2\sqrt{2}x_1 + 2\sqrt{2}y_1 - 2\sqrt{2}x_1 + 2\sqrt{2}y_1 = 4\sqrt{2}y_1$$
Logo, a equação da cônica no novo referencial fica:

$$2x_1^2 + 4\sqrt{2}y_1 - 4 = 0 \Rightarrow x_1^2 = -2\sqrt{2}y_1 + 2 \Rightarrow x_1^2 = -2 \sqrt{2}\left( y_1 - \frac{\sqrt{2}}{2}\right)$$
Fazendo uma nova mudança de referencial $x_2 = x_1$ e $y_2 = y_1 - \frac{\sqrt{2}}{2}$. A equação se reduz a:

$$x_2^2 = -2\sqrt{2}y_2$$
Portanto, podemos classificar a cônica como uma parábola. O foco da parábola no sistema de coordenadas $x_2y_2$ é $\left( 0, -\frac{\sqrt{2}}{2}\right)$. E logo, no sistema $x_1y_1$ o foco é $(0,0)$ e portanto, no sistema $xy$ o foco da parábola é a origem $(0,0)$. O vértice da parábola é a origem do sistema $x_2y_2$.

A cônica $x^2 - 2xy + 4y^2 + 4x + 4y - 4 = 0$ é uma parábola.

    Exemplo 3: Considere a cônica de equação geral:

$$5x^2 + 6xy + 5y^2 - 4x + 4y - 4 = 0$$
Escrevendo esta equação na forma matricial, temos:

$$\left[ \begin{array}{cc} x & y \end{array}\right] \; \left[ \begin{array}{rr} 5 & 3 \\ 3 & 5 \end{array}\right] \; \left[ \begin{array}{c} x \\ y \end{array}\right] + \left[ \begin{array}{cc} -4 & 4 \end{array}\right] \; \left[ \begin{array}{c} x \\ y \end{array}\right] - 4 = 0$$
Vamos diagonalizar a matriz

$$M = \left[ \begin{array}{rr} 5 & 3 \\ 3 & 5 \end{array}\right]$$
para eliminar o termo misto da equação. O polinômio característico de M é dado por:

$$p(\lambda) = det(M - \lambda I_2) = \left| \begin{array}{cc} 5-\lambda & 3 \\ 3 & 5-\lambda \end{array}\right| = (5-\lambda)^2 -9 = \lambda^2 -10\lambda + 16$$
as raízes do polinômio característico são dadas por:

$$p(\lambda) = 0 \Leftrightarrow \lambda^2 - 10\lambda + 16 = 0 \Leftrightarrow \lambda = \frac{10 \pm \sqrt{36}}{2} \Rightarrow \lambda = 2 \;\; ou \;\; \lambda = 8$$
Assim, $\lambda_1 = 2$ e $\lambda_2 = 8$ são autovalores de M. Para o autovalor $\lambda_1$, temos:

$$Mv = \lambda_1 v \Leftrightarrow \left[ \begin{array}{rr} 5 & 3 \\ 3 & 5 \end{array}\right] \; \left[ \begin{array}{c} v_1 \\ v_2 \end{array}\right] = \lambda_1 \left[ \begin{array}{c} v_1 \\ v_2 \end{array}\right] \Leftrightarrow \left[ \begin{array}{r} 5v_1+3v_2 \\ 3v_1+5v_2 \end{array}\right] = \left[ \begin{array}{c} 2v_1 \\ 2v_2 \end{array}\right] \Leftrightarrow$$
$$\Leftrightarrow \left\lbrace \begin{array}{r} 5v_1+3v_2 = 2v_1\\ 3v_1+5v_2 = 2v_2 \end{array} \right. \Leftrightarrow v_2 = -v_1$$
Assim, os autovetores de M associados ao autovalor $\lambda_1 = 2$ são da forma:

$$v = v_1 \; \left[ \begin{array}{r} 1 \\ -1 \end{array}\right]$$
E um vetor normalizado é:

$$v = \left[ \begin{array}{r} \frac{\sqrt{2}}{2} \\ -\frac{\sqrt{2}}{2} \end{array}\right]$$
Para o autovalor $\lambda_2 = 8$, temos:

$$Mw = \lambda_2 w \Leftrightarrow \left[ \begin{array}{rr} 5 & 3 \\ 3 & 5 \end{array}\right] \; \left[ \begin{array}{c} w_1 \\ w_2 \end{array}\right] = \lambda_2 \left[ \begin{array}{c} w_1 \\ w_2 \end{array}\right] \Leftrightarrow \left[ \begin{array}{r} 5w_1+3w_2 \\ 3w_1+5w_2 \end{array}\right] = \left[ \begin{array}{c} 8w_1 \\ 8w_2 \end{array}\right] \Leftrightarrow \left\lbrace \begin{array}{r} 5w_1+3w_2 = 8w_1\\ 3w_1+5w_2 = 8w_2 \end{array} \right. \Leftrightarrow w_2 = w_1$$
Assim, os autovetores de M associados ao autovalor $\lambda_2 = 2$ são da forma:

$$w = w_1 \; \left[ \begin{array}{r} 1 \\ 1 \end{array}\right]$$
E um vetor normalizado é:

$$w = \left[ \begin{array}{r} \frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} \end{array}\right]$$
Portanto, a matriz M é diagonalizável e temos U a matriz diagonalizante e D a matriz diagonal dadas por:

$$U = \left[ \begin{array}{rr} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\ -\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{array}\right] \;\;\;\;\;\; e \;\;\;\;\;\; D = \left[ \begin{array}{cc} 2 & 0 \\ 0 & 8 \end{array}\right]$$
Temos $A = UDU^{-1} \Rightarrow D = U^{-1}AU = U^tAU$. Vamos realizar uma mudança de referencial da base canônica do $R^2$ para a base de autovetores $\left\lbrace \left( \frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2} \right), \left( \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right) \right\rbrace$. A matriz U é a matriz que a realiza a mudança de base. Observe que os vetores dessa nova base são ortonormais e irão formar os eixos diretores da cônica. Esses eixos estão rotacionados com relação aos eixos canônicos, e U é a matriz de rotação. Assim, temos:

$$\left\lbrace \begin{array}{c} \sin{\theta} = \frac{\sqrt{2}}{2} \\ \cos{\theta} = \frac{\sqrt{2}}{2} \end{array}\right. \Rightarrow \theta = \frac{\pi}{4}$$
Ou seja, a cônica está rotacionada de um ângulo $\theta = \frac{\pi}{4} = 45^o$, no sentido horário, com relação aos eixos canônicos.
Agora, como U é a matriz de mudança de base, um ponto $(x_1,y_1)$ no novo referencial é escrito como:

$$\left[ \begin{array}{c} x \\ y \end{array}\right] = U \; \left[ \begin{array}{c} x_1 \\ y_1 \end{array}\right]$$
Logo, substituíndo na forma quadrática da equação da cônica:

$$\left[ \begin{array}{cc} x & y \end{array}\right] \; \left[ \begin{array}{rr} 5 & 3 \\ 3 & 5 \end{array}\right] \; \left[ \begin{array}{c} x \\ y \end{array}\right] = \left[ \begin{array}{cc} x_1 & y_1 \end{array}\right] \; U^t \; \left[ \begin{array}{rr} 5 & 3 \\ 3 & 5 \end{array}\right] \; U \; \left[ \begin{array}{c} x_1\\ y_1 \end{array}\right] =$$
$$= \left[ \begin{array}{cc} x_1 & y_1 \end{array}\right] \; \left[ \begin{array}{rr} 2 & 0 \\ 0 & 8 \end{array}\right] \; \left[ \begin{array}{c} x_1\\ y_1 \end{array}\right] = 2x_1^2 + 8y_1^2$$
E na forma linear temos:

$$\left[ \begin{array}{cc} -4 & 4 \end{array}\right] \; \left[ \begin{array}{c} x \\ y \end{array}\right] = \left[ \begin{array}{cc} -4 & 4 \end{array}\right] \; \left[ \begin{array}{rr} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\ -\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{array}\right] \; \left[ \begin{array}{c} x_1\\ y_1 \end{array}\right] = \left[ \begin{array}{cc} -4 & 4 \end{array}\right] \; \left[ \begin{array}{r} \frac{\sqrt{2}}{2}x_1 + \frac{\sqrt{2}}{2}y_1 \\ -\frac{\sqrt{2}}{2}x_1 + \frac{\sqrt{2}}{2}y_1 \end{array}\right] =$$
$$= -2\sqrt{2} x_1 -2\sqrt{2}y_1 -2\sqrt{2}x_1 + 2\sqrt{2}y_1 = -4\sqrt{2}x_1$$
Portanto, a equação da cônica no referencial $x_1y_1$ fica:

$$2x_1^2 + 8y_1^2 -4\sqrt{2}x_1 -4 = 0$$
Completando o quadrado para o termo em $x_1$ temos:

$$2x_1^2 - 4\sqrt{2}x_1 = 2 \left( x_1^2 - 2\sqrt{2}x_1\right) = 2 \left( x_1^2 - 2\sqrt{2}x_1 + 2 - 2\right) = 2 \left( \left( x_1 - \sqrt{2}\right)^2 - 2\right) =$$
$$= 2 \left( x_1 - \sqrt{2}\right)^2 - 4$$
Fazendo uma nova mudança de referencial: $x_2 = x_1 - \sqrt{2}$ e $y_2 = y_1$, e substituindo na equação da cônica, temos:

$$2x_2^2 + 8y_2^2 = 8 \Rightarrow \frac{x_2^2}{4} + y_2^2 = 1$$
Portanto, podemos identificar a cônica como sendo uma elipse, com eixo maior igual a 2 e eixo menor igual a 1, rotacionada de um ângulo de $45^o$ no sentido horário e transladada uma distância $\sqrt{2}$ em relação ao eixo $x_1$, cujo vetor diretor é $v = \left( \frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2}\right)$, logo, a elipse está centrada em $(1,-1)$.

A cônica $5x^2 + 6xy + 5y^2 - 4x + 4y - 4 = 0$ é uma elipse.