Transformações Lineares

Aplicações

    Definição: Dados dois conjuntos, não vazios, U e V, uma aplicação de U em V é uma "lei" que associa a cada elemento de U um único elemento de V. Se denotamos por F esta aplicação, então, o elemento associado a $u \in U$ é denotado por $F(u)$, que está em V, denominado a imagem de u pela aplicação F.

    U é o domínio e V o contra-domínio da aplicação F. Denotamos a aplicação da forma: $F: U \rightarrow V$. Ou ainda, indicando por u um elemento qualquer de U, denotamos: $u \mapsto F(u)$.

    Denomina-se Imagem da aplicação $F: U \rightarrow V$ o subconjunto de V dado por: $Im(F) = \left\lbrace F(u)\mid u \inU \right\rbrace,$ ou seja, são todos os elementos em V que são associados a algum elemento de U pela aplicação F.

    Duas aplicações F e G são iguais se, e somente se, possuem o mesmo domínio e $F(u) = G(u)$ para todo u neste domínio.

    Aplicação Injetora: Uma aplicação $F: U \rightarrow V$ é Injetora se, e somente se:

$$F(u_1) = F(u_2) \Rightarrow u_1 =u_2, \;\;\;\; \forall u_1, u_2 \in U$$ 
ou, se e somente se:
$$u_1 \neq u_2 \Rightarrow F(u_1)\neq F(u_2), \;\;\;\; \forall u_1, u_2 \in U$$

    Aplicação Sobrejetora: Uma aplicação $F: U \rightarrow V$ é Sobrejetora se, se somente se, $Im(F) = V$, ou seja, para todo $v \in V$ existe $u \in U$ tal que $F(u) = v$.

    Aplicação Bijetora: Uma aplicação $F: U \rightarrow V$ é Bijetora se, e somente se, é Injetora e é Sobrejetora.

    Voltar ao Topo.

Transformações Lineares

Exemplos

    Exemplo 1: A seguinte aplicação de $R^2$ em $R^2$ é uma transformação linear:

$$\begin{array}{llll} T: & R^2& \longrightarrow & R^2 \\ & v &\longmapsto & T(v) = \alpha v \end{array}$$
que é uma expansão (ou contração), dependendo do valor $\alpha$. Esta transformação leva cada vetor v do $R^2$ num vetor de mesma direção de v, mas com sentido igual a v (caso $\alpha > 0$) ou sentido oposto (caso $\alpha < 0$) e módulo maior (caso $|\alpha| > 1$) ou menor (caso $|\alpha| < 1$). Para $\alpha = 1$ esta é a transformação identidade, que leva o vetor v nele mesmo.

    De fato, para todo $v_1, v_2 \in R^2$ e $\beta \in R$, temos:

$$T(v_1 + \beta v_2) = \alpha(v_1 +\beta v_2) = \alpha v_1 + \alpha \beta v_2 =T(v_1) + \beta T(v_2)$$
Assim, T é uma transformação linear.

Por exemplo, para $\alpha = 2$, e $v = (x, y) \in R^2$, temos: $T(x, y) = 2(x, y)$.

A transformação linear T leva todo elemento $(x,y) \in R^2$ no elemento $2(x,y)$.

Esta transformação aplicada a uma figura (conjunto de pontos do $R^2$) irá expandir esta figura no dobro de seu tamanho.

A transformação linear T leva uma figura no plano na mesma figura ampliada com o dobro do tamanho.

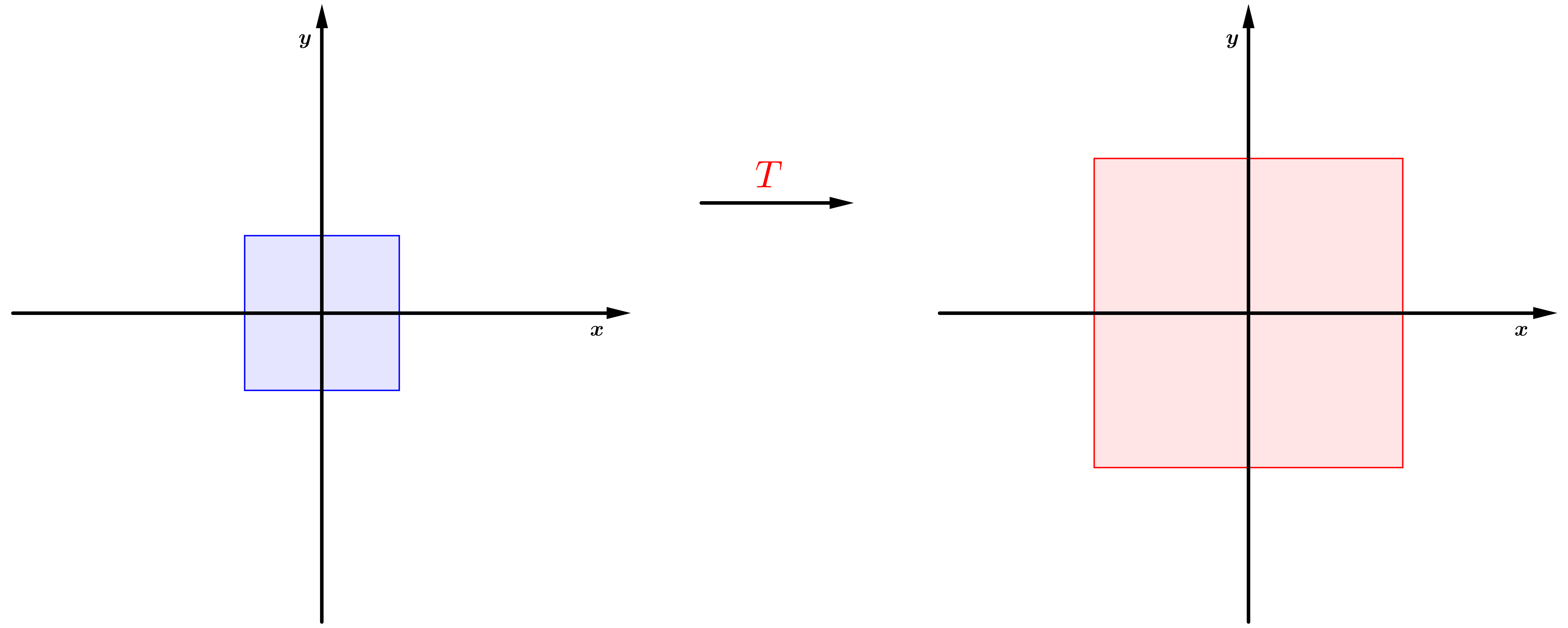
    Exemplo 2: A seguinte aplicação de $R^2$ em $R^2$ é uma transformação linear:

$$\begin{array}{llll} T: & R^2& \longrightarrow & R^2 \\ & (x, y)& \longmapsto & T((x,y)) = (x, -y)\end{array}$$
que é uma reflexão em torno do eixo x.

    De fato, T é transformação linear, uma vez que, para todo $v_1 = (x_1, y_1), v_2 = (x_2, y_2)\in R^2$ e $\alpha \in R$, temos:

$$T(v_1 + \alpha v_2) = T((x_1,y_1) +\alpha(x_2, y_2)) = T(x_1 + \alpha x_2, y_1 +\alpha y_2) = (x_1 + \alpha x_2, -y_1 - \alpha y_2$$ $$= (x_1, -y_1) + (\alpha x_2,-\alpha y_2) = (x_1, -y_1) + \alpha (x_2, -y_2) =T(x_1, y_1) + \alpha T(x_2, y_2) = T(v_1) + \alphaT(v_2)$$
onde usamos o fato de que $R^2$ é espaço vetorial e a forma como foi definida a aplicação T.

A transformação linear T é a reflexão em torno do eixo x.

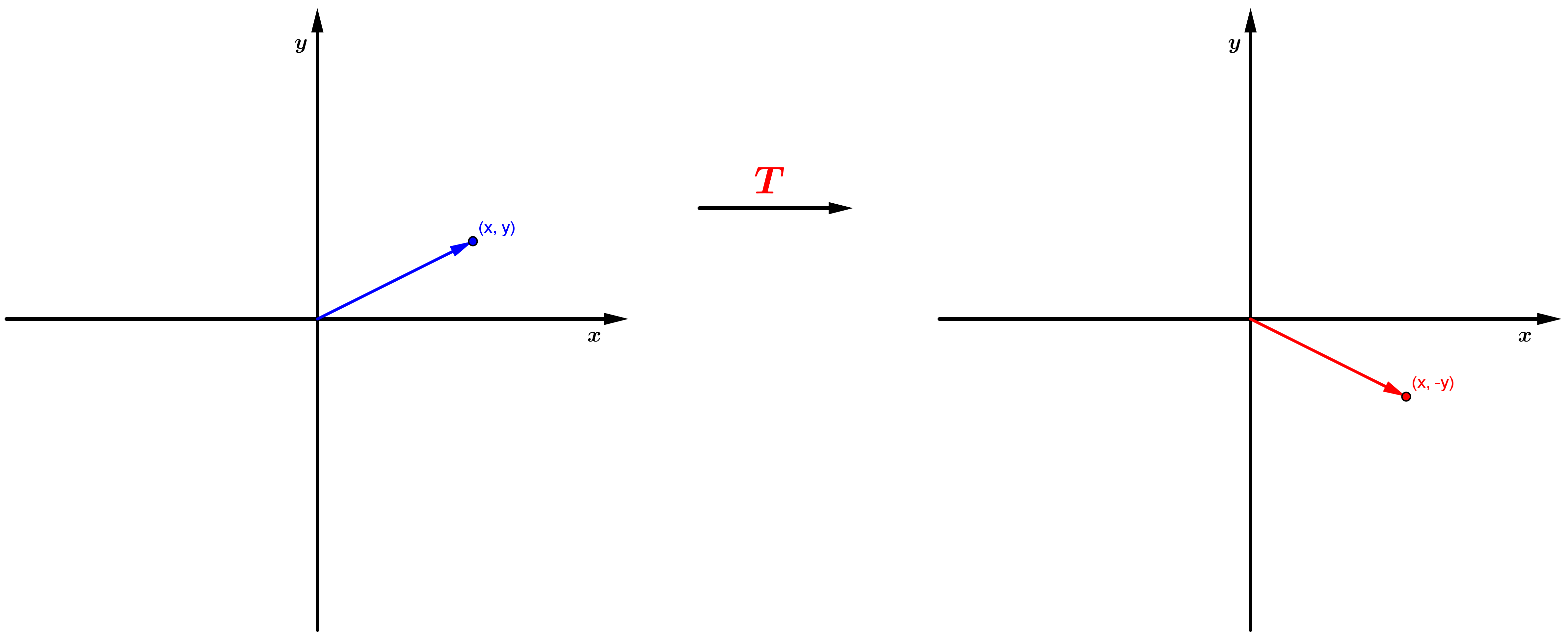
    Considere agora um triângulo ABC de vértices A = (-1, 4), B = (3, 1) e C = (2, 6). Vamos aplicar a transformação linear T neste triângulo. Para saber qual a imagem do triângulo pela transformação, basta sabermos as imagens de seus vértices:

T(-1, 4) = (-1, -4)
T(3, 1) = (3, -1)
T(2, 6) = (2, -6)

Portanto, o triângulo ABC é levado no triângulo A'B'C', com A' = (-1, -4), B' = (3, -1) e C' = (2, -6), pela transformação linear T, que é a reflexão em torno do eixo x.

A transformação linear T leva o triângulo ABC no triângulo A'B'C'.

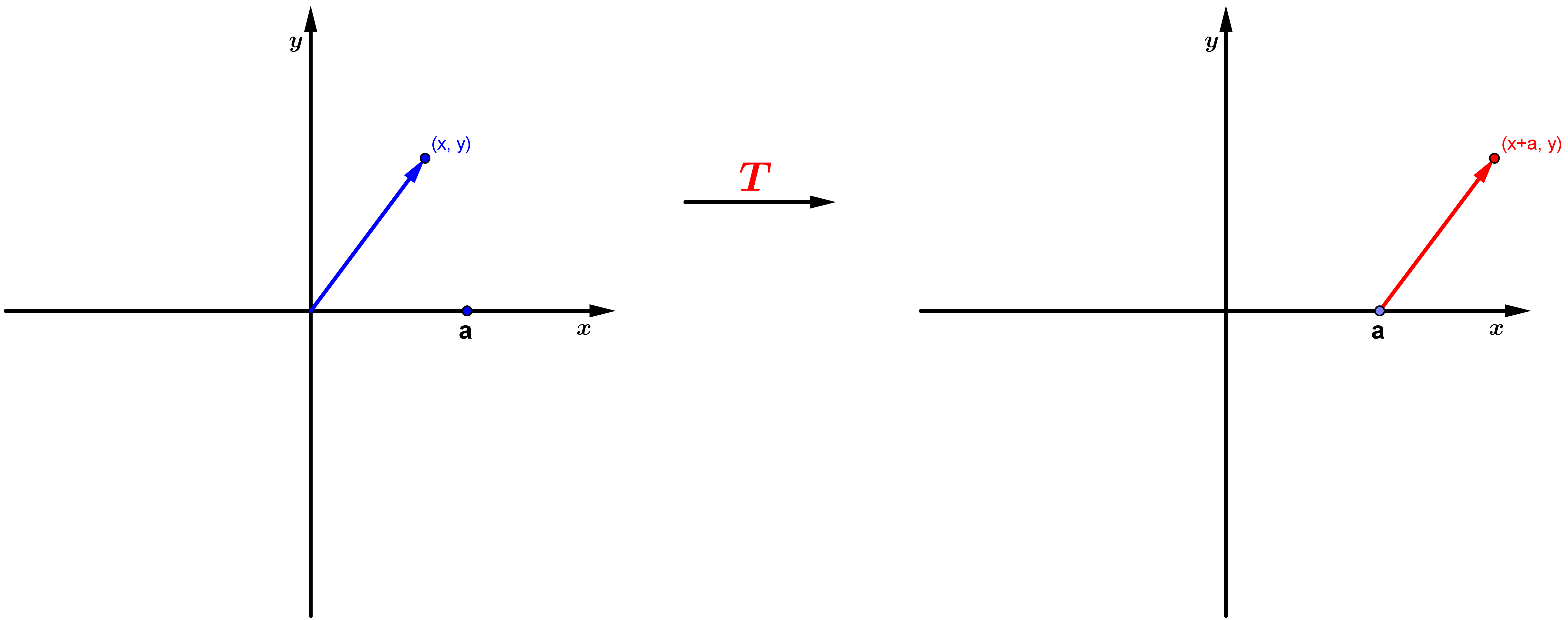
    Exemplo 3: Considere a seguinte aplicação:

$$\begin{array}{llll} T: & R^2& \longrightarrow & R^2 \\ & (x, y)& \longmapsto & T(x, y) = (x + a, y)\end{array}$$
com $a \in R$, que é uma translação de comprimento $a$ e direção do eixo x. Essa aplicação NÃO é uma transformação linear, a menos que $a = 0$, pois não satisfaz as condições para ser linear.

    Considere $v_1 = (x_1,y_1)$ e $v_2 = (x_2, y_2)$ pertencentes a $R^2$, temos que:

$$T(v_1 + v_2) = T((x_1, y_1) + (x_2,y_2)) = T(x_1+x_2, y_1+y_2) = (x_1 + x_2 + a,y_1+y_2)$$
mas por outro lado,

$$T(v_1) + T(v_2) = T(x_1, y_1) +T(x_2, y_2) = (x_1 + a, y_1) + (x_2 + a, y_2) =(x_1 + x_2 + 2a, y_1+y_2)$$
Ou seja, $T(v_1+v_2) \neq T(v_1) + T(v_2)$, para $a \neq 0$, logo a aplicação T não é uma transformação linear.

A aplicação T é a translação de comprimento a e direção do eixo x. T não é transformação linear.

    Exemplo 4: Considere a transformação linear $T:R^2 \longrightarrow R^2$ tal que:

$$T(1,0) = (1, 0),\;\;\;\;\;\;\; T(0, 1) = (2, 1)$$
Vamos determinar explicitamente a transformação linear T.

    Estamos considerando o espaço vetorial $R^2$ com a base canônica $B = \left\lbrace (1, 0), (0, 1)\right\rbrace$. Podemos escrever um elemento qualquer de $R^2$ de forma única como:

$$(x, y) = x(1, 0) + y(0,1)$$
Sabendo como a transformação T atua nos elementos da base B, e que T é transformação linear, temos que:

$$T(x, y) = T(x(1, 0) + y(0, 1))= x T(1, 0) + y T(0, 1) \Rightarrow$$$$\Rightarrow T(x, y) = x (1, 0)+ y(2, 1) \Rightarrow T(x, y) = (x+2y, y)$$
Assim, obtemos a expressão da transformação linear T.

    Considere o quadrado de vértices A = (0, 0), B = (1, 0), C = (1, 1) e D = (0, 1). Temos que as imagens dos vértices do quadrado pela transformação T são:

$$T(0, 0) = (0, 0), \;\;\; T(1,0) = (1, 0), \;\;\; T(1, 1) = (3, 1), \;\;\;T(0, 1) = (2, 1)$$
Assim, o quadrado ABCD é levado no paralelogramo A'B'C'D'  de vértices A' = (0, 0), B' = (1, 0), C' = (3, 1) e D' = (2, 1) pela transformação linear T.

A transformação linear T leva o quadrado ABCD no paralelogramo A'B'C'D'.

    Veja estes e mais exemplos AQUI.

    Voltar ao Topo.