Definição
Sejam U
e W subespaços vetoriais de um espaço vetorial V. A
Intersecção dos subespaços U e W é:
e
Demonstração: AQUI.
Exemplos
Exemplo 1: Considere os subespaços e . A intersecção de U e W é:
Ou seja,
.
Geometricamente, U é o eixo y dos eixos coordenados,
pois são os elementos de
que tem a primeira coordenada nula e W é o eixo x,
pois são os elementos de
que tem a segunda coordenada nula.
Assim, a intersecção
é a origem
.
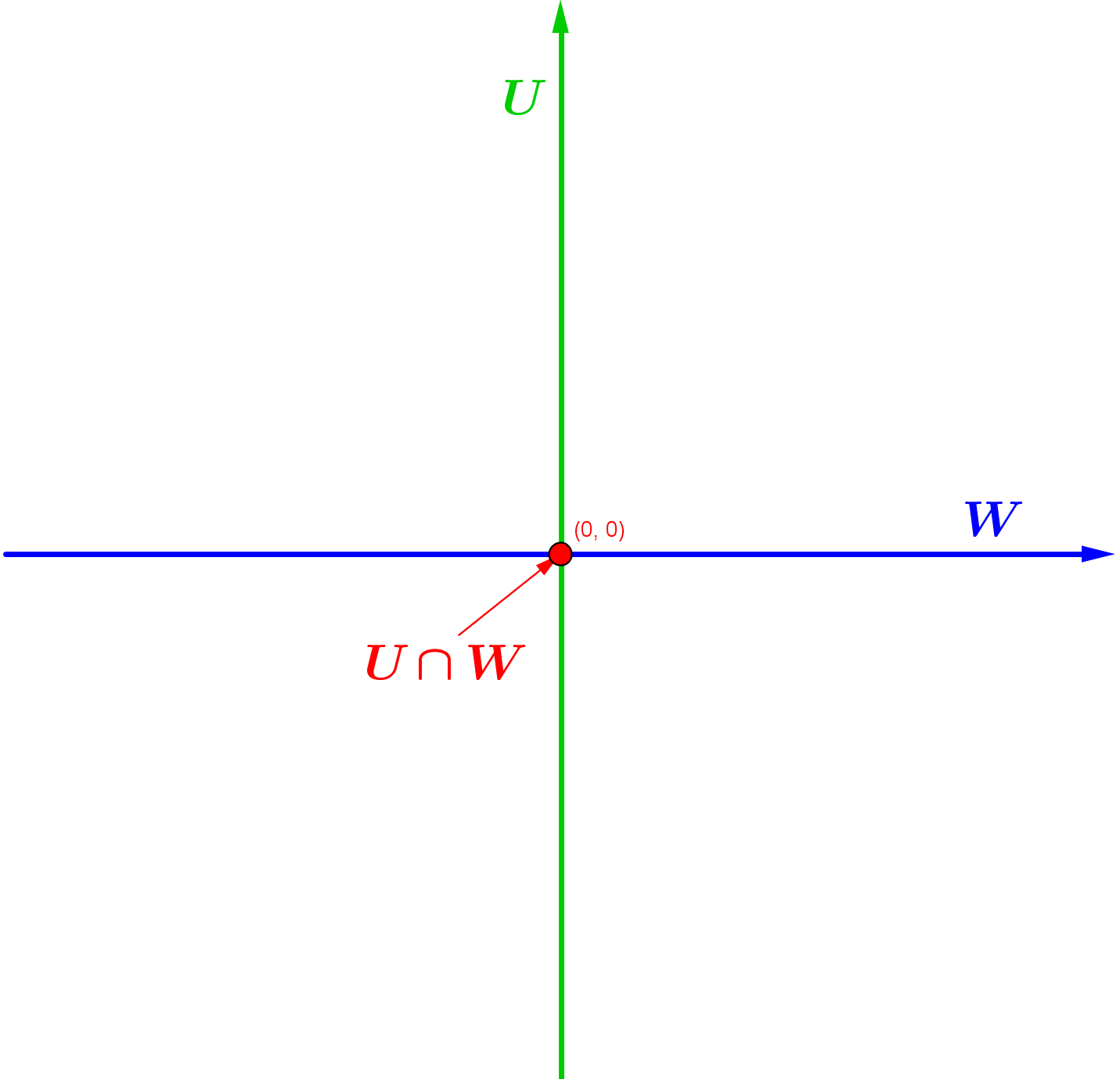
A origem (0,0) é a intersecção dos subespaços U e W.
Exemplo 2:
Dados os subespaços
e .
A intersecção dos subespaços U e W é:
Geometricamente, U é o plano
yz e W é o plano xy. A intersecção é a intersecção desses planos, que é o
eixo y, que de fato é um subespaço vetorial de .

A intersecção dos subespaços U e W é o eixo y dos eixos coordenados.
Exemplo
3: Sejam
e subespaços
de .
Determine a intersecção .
Um elemento de
,
que pertence a intersecção de U e W deve
satisfazer todas as condições dos dois
conjuntos U e W ao mesmo tempo, ou seja, suas
componentes devem satisfazer o sistema:
Substituindo a primeira e
a segunda equações na terceira equação,
teremos: . Assim, ficamos com as
condições: e , com livres. Logo:
Podemos também dar um
valor para a variável z que está livre, por
exemplo , assim teremos e , logo a intersecção será o subespaço gerado pelo vetor
, ou seja, .
Veja estes e mais
exemplos AQUI.
União de
Subespaços Vetoriais
Observação:
Quando se fala em conjuntos, é comum pensarmos
também na união desses conjuntos. Uma vez que
a intersecção de dois subespaços é um
subespaço vetorial, esperamos o mesmo da união
dos subespaços, mas isso não ocorre. Tomando
um elemento
e um elemento
que não está em U, ou seja, U não está contido
em W ou vice-versa, não podemos afirmar nada
sobre o elemento
,
não necessariamente ele estará na união
.
Assim,
não satisfaz todas as condições de subespaço
vetorial. Portanto, a união de dois subespaços
vetoriais NÃO é um subespaço vetorial.
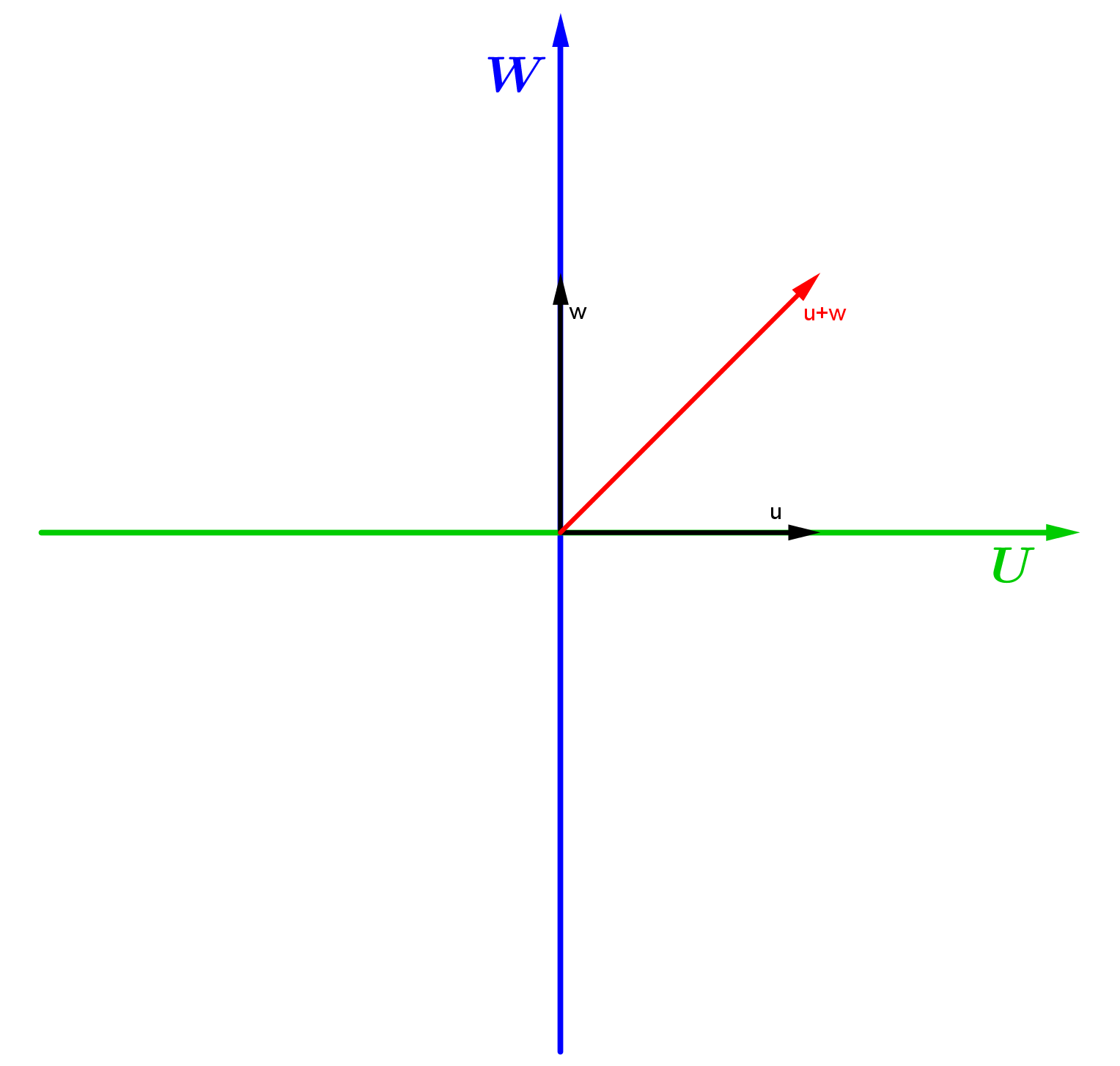
Exemplo: Sejam os subespaços e . A união entre U e W será o conjunto:
O elemento neutro
está em U e em W e logo, está também na união.
Mas, tome os elementos
,
não podemos garantir que a soma dos vetores u
e w estará em
.
Por exemplo, considere
e
.
Temos que
,
mas
,
que é um vetor que não satisfaz nenhuma das
condições do conjunto da união, logo
.