Núcleo e Imagem

Definições

    Definição: Seja T uma transformação linear, $T: U \longrightarrow V$, com U e V espaços vetoriais sobre um corpo $K$. O Núcleo da transformação linear T, denotado por $\mathcal{N}(T)$ ou $Ker(T)$ é o seguinte subconjunto do domínio U:

$$\mathcal{N}(T) = \left\lbrace u \in U \mid T(u) = e_V \right\rbrace$$
com $e_V$ o elemento neutro do espaço vetorial V.

    Teorema: Seja $T:U \longrightarrow V$ uma transformação linear. O conjunto $\mathcal{N}(T)$, núcleo da transformação linear T é um subespaço vetorial de U.

    Demonstração: AQUI.

   
    Definição: Seja T uma transformação linear, $T: U \longrightarrow V$, com U e V espaços vetoriais sobre um corpo $K$. A Imagem da transformação linear T é o seguinte subconjunto do contra-domínio V:

$$Im(T) = \left\lbrace v \in V \mid v = T(u) \;\;\;\; para \; algum \;\;\;\; u \in U \right\rbrace$$ 

    Teorema: Seja $T:U \longrightarrow V$ uma transformação linear. O conjunto $Im(T)$, imagem da transformação linear T é um subespaço vetorial de V.

    Demonstração: AQUI.

Exemplos

    Exemplo 1: Considere a transformação linear:

$$\begin{array}{llll} T: & R^2 & \longrightarrow & R \\ & (x, y) & \longmapsto & T(x, y) = 3x + 2y \end{array}$$ 
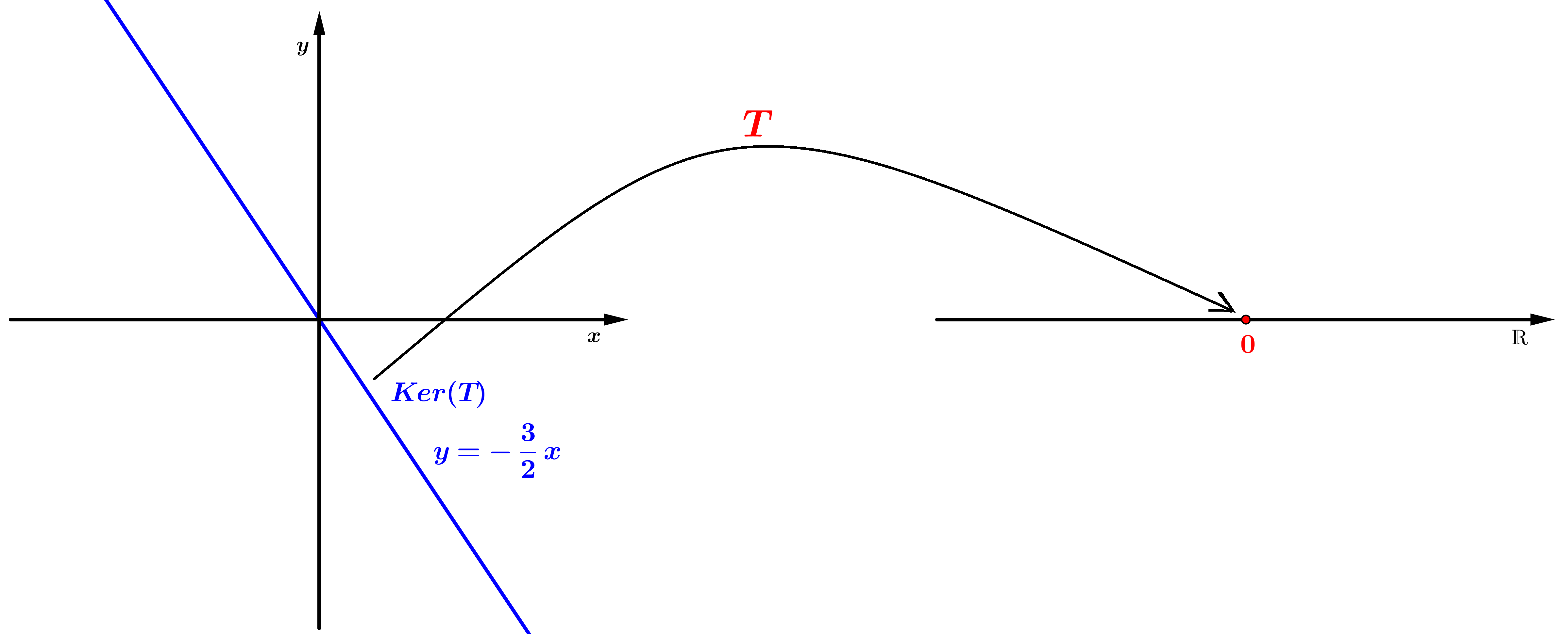
Vamos determinar o núcleo da transformação linear T.

    Um elemento de $R^2$ está no núcleo se a transformação T o transforma no elemento neutro de $R$, ou seja:

$$T(x,y) = 3x + 2y = 0 \Rightarrow y = - \frac{3}{2} x$$
Assim, a reta $y = - \frac{3}{2} x$, subespaço vetorial, de $R^2$, é o núcleo da transformação linear T.

A reta $y = - \frac{3}{2} x$ é o núcleo da transformação linear T.

    Exemplo 2: Considere a transformação linear:

$$\begin{array}{llll} T: & R^3 & \longrightarrow & R^2 \\ & (x, y, z) & \longmapsto & T(x, y, z) = (x - y -z, 2z - x) \end{array}$$
Vamos determinar a imagem da transformação linear T.

Todo elemento do contra-domínio $R^2$ pertence a imagem de T se for da forma:

$$(x - y -z, 2z - x) = x(1, -1) + y(-1, 0) + z(-1, 2)$$
Logo, temos que $Im(T) = [(1, -1), (-1, 0), (-1, 2)]$. Escalonando esses geradores da imagem, como linhas de uma matriz, para obtermos uma base, temos:

$$\left[ \begin{array}{cc} 1 & -1 \\ -1 & 0 \\ -1 & 2 \end{array} \right] \rightarrow \left[ \begin{array}{cc} 1 & -1 \\ 0 & -1 \\ 0 & 1 \end{array} \right] \rightarrow \left[ \begin{array}{cc} 1 & -1 \\ 0 & -1 \\ 0 & 0 \end{array} \right]$$
E, portanto, $\left\lbrace (1, -1), (0, -1) \right\rbrace$ é uma base para $Im(T)$ e $dim(Im(T)) = 2 = dim(R^2)$. Como $Im(T)$ é um subespaço do $R^2$ e tem a mesma dimensão que $R^2$, concluímos que $Im(T) = R^2$.


    Veja estes e mais exemplos AQUI.

    Voltar ao Topo.