Definição
Sejam V um espaço vetorial sobre R e um conjunto finito de elementos de V. Dizemos que o conjunto S é Linearmente Independente (L.I.), ou que os elementos são Linearmente Independentes, se a equação:
com o
elemento neutro de V e
possui somente a solução
.
Caso contrário, ou seja, quando
existe pelo menos um
,
dizemos que o conjunto S é Linearmente Dependente
(L.D.), ou que os elementos
são
Linearmente Dependentes.
Propriedades
Seja V um espaço
vetorial sobre R. Valem as seguintes propriedades:
(P1) Se um conjunto finito de elementos de V contém o elemento neutro de V, este conjunto é L.D.
(P2) Se , com , então S é L.I.
(P3) Se é L.D., então um dos seus elementos é combinação linear dos demais.
(P4) Sejam
e
subconjuntos finitos e não vazios de V. Se
é L.D. e
,
então
também é L.D.
(P5) Sejam e subconjuntos finitos e não vazios de V. Se é L.I. e , então também é L.I.
(P6) Se é L.I., e para algum tivermos que é L.D., então o elemento é combinação linear dos elementos de S.
(P7) Se
e
,
então
.
Esta última propriedade nos diz que se
um elemento de um conjunto de geradores é combinação
linear dos demais, ele pode ser extraído do conjunto de
geradores, pois o subespaço gerado ainda é o mesmo.
Demonstrações:
AQUI.
Exemplos
Exemplo 1: Os
elementos
e
do espaço vetorial
são Linearmente Dependentes.
De fato, temos que a equação:
É verdadeira para
e .
Assim,
e
são L.D.
Também podemos verificar que: ou
seja,
é combinação linear de
.
Geometricamente, quando dois
elementos em
ou
são Linearmente Dependentes,
eles estão na mesma reta,
quando colocados na mesma origem.
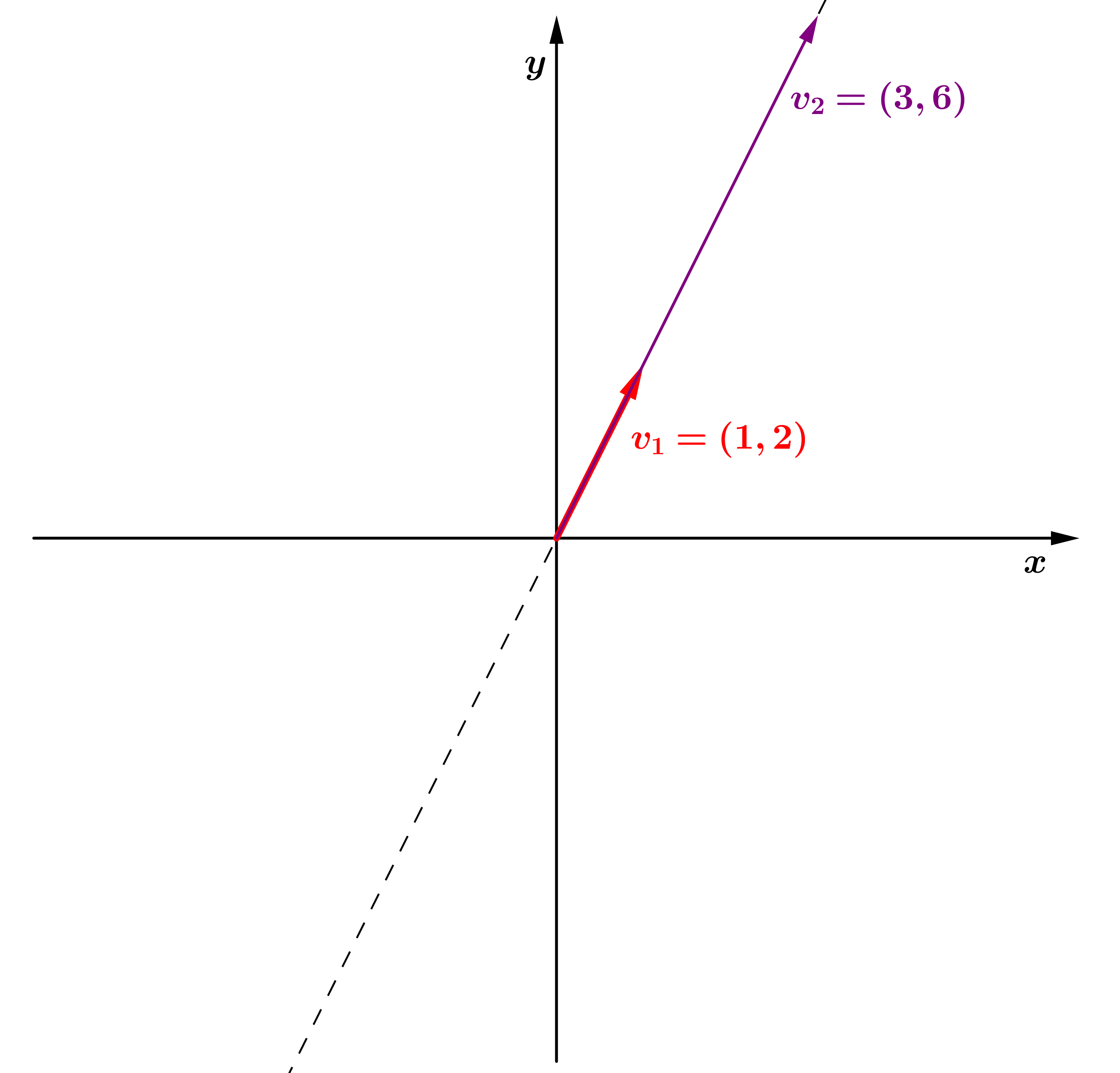
Os vetores e são L.D.
De fato, a equação:
Vale apenas para .
Geometricamente, quando dois elementos em ou são L.I., eles não estão na mesma reta, quando colocados na mesma origem.
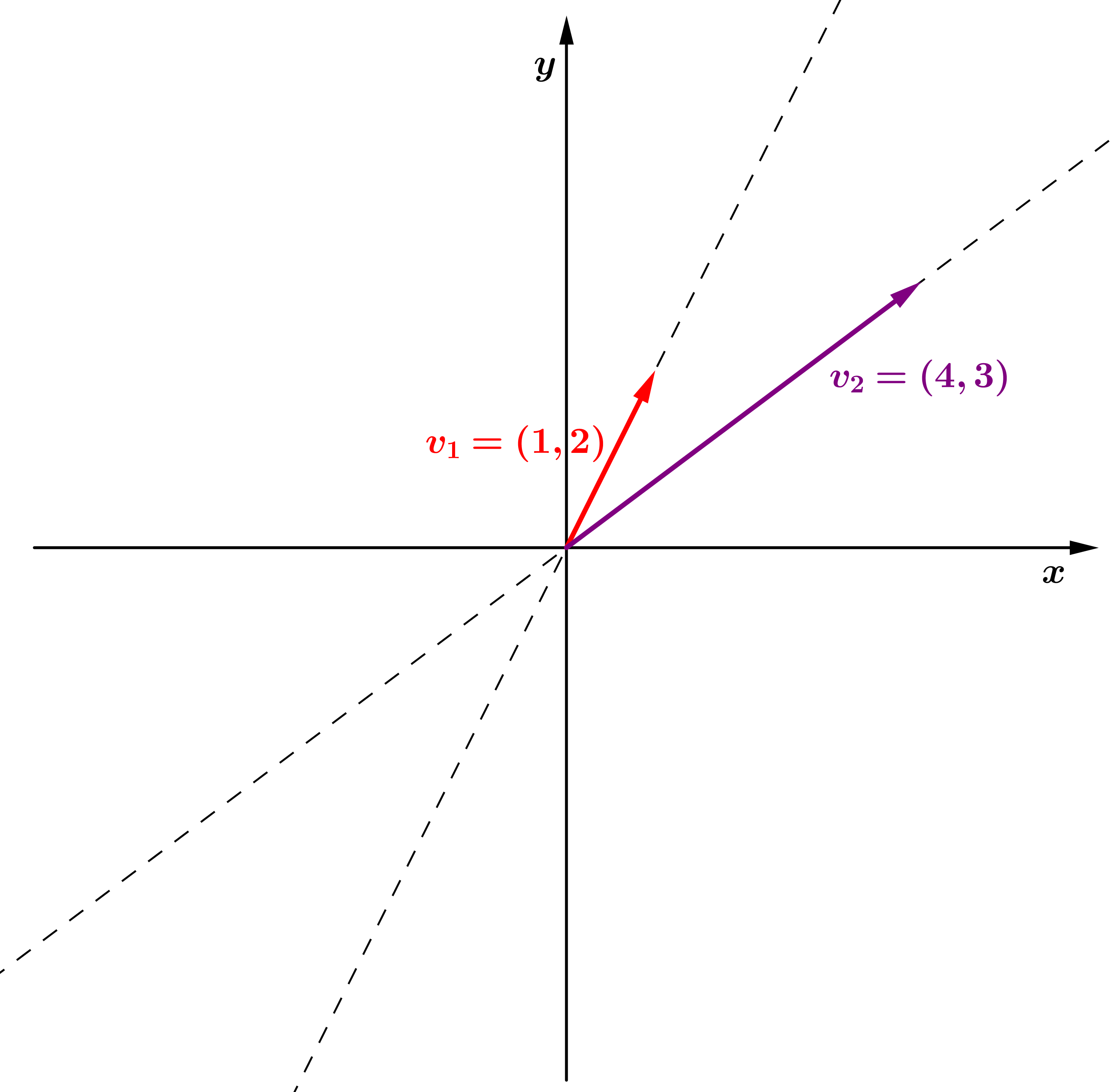
Os vetores e são L.I.
Tome a equação:
Obtemos um sistema linear que tem como solução: e com livre. Assim, para algum a equação vale, portanto , e são L.D.
De fato, podemos ver que o vetor é combinação linear dos vetores e , uma vez que: .
Geometricamente, se três vetores em são Linearmente Dependentes, eles estão no mesmo plano, quando colocados na mesma origem. Caso contrário, ou seja, se forem Linearmente Independentes, os vetores não estão no mesmo plano, quando colocados na mesma origem.
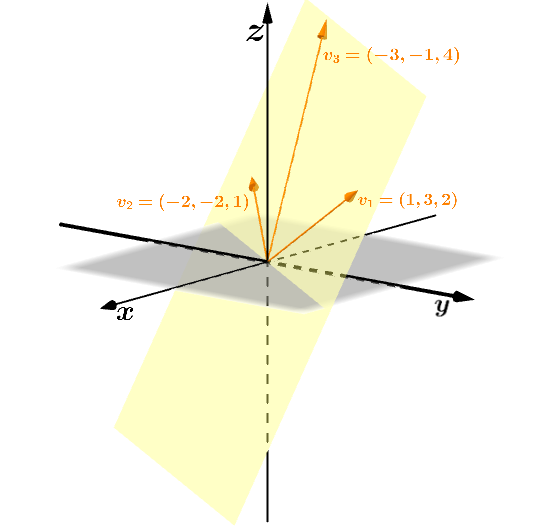
Os vetores , e são L.D.
Veja estes e mais exemplos AQUI.
Voltar ao Topo.