Quadrados Mínimos

Em diversas situações é comum que a solução de um problema leve a um sistema linear que teoricamente deveria ser consistente, mas que na prática não é, devido a erros em medições ou aproximações. Sistemas inconsistentes ou impossíveis são aqueles que não possuem nenhuma solução exata.

Um sistema

Ax = b

inconsistente também é importante em aplicações e, como não podemos obter sua solução exata, surge a necessidade de obtermos um elemento

\bar{x}

que chegue o mais próximo possível de ser uma solução, no sentido de que minimiza o erro de aproximação.

Sistemas inconsistentes são geralmente da forma

Ax = b

, onde

A \in \mathbb{M}_{m \times n}(\mathbb{R})

com

m > n

, isto é, com mais equações do que incógnitas. Queremos encontrar um elemento

\bar{x} \in \mathbb{R}^n

de modo que:

\left\| A\bar{x} - b \right\|_2 = \min\left\lbrace \left\| Ax - b \right\|_2 \mid x \in \mathbb{R}^n \right\rbrace

Dizemos que o elemento

\bar{x}

é uma solução de quadrados mínimos para o sistema

Ax = b

. Se o sistema é consistente e

\bar{x}

é uma solução exata, então o erro é nulo, pois

\left\| A\bar{x} - b \right\|_2 = 0

.

Seja

r = Ax - b

o vetor resíduo que resulta da aproximação

x

como solução do sistema

Ax = b

. Se

r = \left(r_1, r_2, ..., r_n\right)

, então uma solução de quadrados mínimos minimiza

\left\| r \right\|_2 = \sqrt{r_1^2 + r_2^2 + ... + r_n^2}

e, portanto, também minimiza:

\left\| r \right\|_2^2 = r_1^2 + r_2^2 + ... + r_n^2

Assim, o problema de encontrar, se possível, um vetor

\bar{x}

que minimiza

\left\| Ax - b \right\|_2

é denominado um problema de quadrados mínimos.

Revisão de Conceitos Básicos

Teorema 1: sejam

W

um subespaço vetorial de dimensão finita de um espaço com produto interno

V

v

um elemento de

V

u

a projeção ortogonal de

v

W

. Então,

u

é o elemento em

W

mais próximo de

v

, no seguinte sentido:

\left\| v - u \right\|_2 < \left\| v - w \right\|_2

para qualquer

w \in W

distinto de

u

.

Definição: Seja

A

uma matriz

m \times n

. O subespaço do

\mathbb{R}^n

gerado pelos vetores linha de

A

é denominado espaço linha de

A

e o subespaço do

\mathbb{R}^m

gerado pelos vetores coluna de

A

é denominado espaço coluna de

A

. O espaço solução do sistema linear homogêneo

Ax = 0

, que é um subespaço do

\mathbb{R}^n

, é denominado espaço nulo de

A

.

Definição: Seja

W

um subespaço vetorial de um espaço com produto interno

V

. O conjunto de todos os elementos

v \in V

que são ortogonais a

W

é denominado complemento ortogonal de

W

.

Teorema 2: Seja

A

uma matriz

m \times n

. Então, o espaço nulo de

A

e o espaço linha de

A

são complementos ortogonais, isto é, um vetor

v \in \mathbb{R}^n

é ortogonal ao espaço linha de

A

se, e somente se,

Av = 0

.

Como o espaço linha de

A

é igual ao espaço coluna de

A^t

, aplicando o resultado anterior à matriz

A^t

, temos que o espaço nulo de

A^t

e o espaço coluna de

A^t

são complementos ortogonais.

As demonstrações destes resultados podem ser vistas AQUI.

Solução de Quadrados Mínimos

Considere um sistema linear

Ax = b

com

m

equações e

n

incógnitas, onde

m > n

. Seja

W

o espaço coluna da matriz

A

. Para cada elemento

x \in \mathbb{R}^n

, o produto

Ax

é uma combinação linear dos vetores coluna de

A

. Dessa forma, à medida que

x

varia sobre o

\mathbb{R}^n

, o elemento

Ax

varia sobre as possíveis combinações lineares dos vetores coluna de

A

, ou seja, varia sobre o espaço coluna

W

. Buscamos encontrar um elemento

\bar{b}

pertencente ao espaço coluna de

A

que minimiza

\left\|b - \bar{b} \right\|_2

.

Geometricamente, resolver o problema de quadrados mínimos do sistema

Ax = b

significa encontrar um vetor

\bar{x} \in \mathbb{R}^n

tal que

\bar{b} = A\bar{x}

é o vetor em

W

mais próximo de

b

, ou seja, que minimiza

\left\|b - Ax\right\|_2

. Do Teorema 1 segue que o vetor em

W

mais próximo de

b

é a projeção ortogonal de

b

W

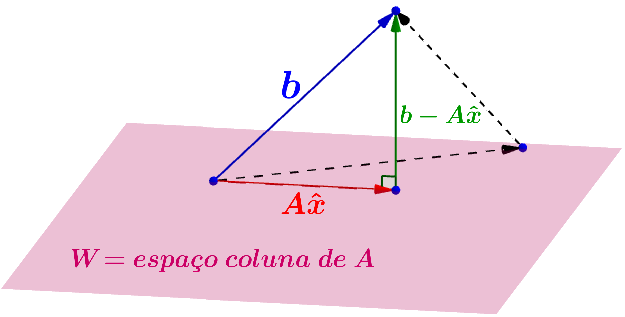
Figura 1: uma solução de quadrados mínimos

\bar{x}

fornece um vetor

A\bar{x} \in W

mais próximo de

b

W

é também o espaço linha de

A^t

e, como

A\bar{x}

é projeção ortogonal de

b

W

, segue que

b - A\bar{x}

é ortogonal a

W

. Pelo Teorema 2,

b - A\bar{x}

está no espaço nulo de

A^t

, ou seja, satisfaz:

A^t(b - A\bar{x}) = 0

Dessa forma, uma solução de quadrados mínimos do sistema

Ax = b

deve satisfazer:

A^t(b - Ax) = 0 \Leftrightarrow A^tAx = A^tb

Este sistema é denominado sistema normal associado ao sistema

Ax = b

. Assim, o problema de encontrar uma solução de quadrados mínimos de um sistema linear corresponde a encontrar uma solução exata do sistema normal associado.

Estudaremos um método para encontrar a solução de quadrados mínimos de um sistema utilizando a fatoração ortogonal, e nesta seção mostramos que o sistema normal associado sempre possui solução, que é única caso a matriz

A

tenha posto completo e infinitas soluções caso a matriz

A

não tenha posto completo.

Voltar ao Topo.

Utilizando a Fatoração de Cholesky

No caso em que matriz

A

tem posto completo, então

A^tA

é simétrica definida positiva e, podemos obter sua fatoração de Cholesky:

A^tA = GG^t

onde

G

é triangular inferior com diagonal positiva. Dessa forma, temos

A^tAx = A^tb \Leftrightarrow GG^tx = A^tb

e a resolução do sistema normal associado segue da resolução dos sistemas triangulares:

(i) \;Gy = A^tb \;\; e \;\;(ii)\; G^tx = y

Exemplo 1: considere o seguinte sistema linear na forma matricial:

Ax = b \Leftrightarrow \left[ \begin{array}{rrr} 2 & 0 & -1 \\ 1 & -2 & 2 \\ 2 & -1 & 0 \\ 0 & 1 & -1 \end{array} \right] \;\left[ \begin{array}{r} x_1 \\ x_2 \\ x_3 \end{array} \right] = \left[ \begin{array}{r} 0 \\ 6 \\ 0 \\ 6 \end{array} \right]

Estamos interessados em encontrar uma solução de quadrados mínimos deste sistema inconsistente. Temos que:

A^tA = \left[ \begin{array}{rrrr} 2 & 1 & 2 & 0 \\ 0 & -2 & -1 & 1 \\ -1 & 2 & 0 & -1 \end{array} \right]\; \left[ \begin{array}{rrr} 2 & 0 & -1 \\ 1 & -2 & 2 \\ 2 & -1 & 0 \\ 0 & 1 & -1 \end{array} \right] = \left[ \begin{array}{rrr} 9 & -4 & 0 \\ -4 & 6 & -5 \\ 0 & -5 & 6 \end{array} \right]

O sistema normal associado ao sistema

Ax = b

é dado por:

A^tAx = A^tb \Leftrightarrow \left[ \begin{array}{rrr} 9 & -4 & 0 \\ -4 & 6 & -5 \\ 0 & -5 & 6 \end{array} \right] \;\left[ \begin{array}{r} x_1 \\ x_2 \\ x_3 \end{array} \right] = \left[ \begin{array}{r} 6 \\ -6 \\ 6 \end{array} \right]

A matriz

A^tA

é simétrica definida positiva e, utilizando uma precisão de 4 casas decimais, obtemos o fator de Cholesky:

G = \left[ \begin{array}{rrr} 3.0000 & 0 & 0 \\ -1.3333 & 2.0548 & 0 \\ 0 & -2.4333 & 0.2810 \end{array} \right]

tal que

A^tA = GG^t

. Assim, temos

A^tAx = A^tb \Leftrightarrow GG^tx = A^tb

. Resolvendo primeiro o sistema triangular inferior:

Gy = A^tb \Leftrightarrow \left[ \begin{array}{rrr} 3.0000 & 0 & 0 \\ -1.3333 & 2.0548 & 0 \\ 0 & -2.4333 & 0.2810 \end{array} \right] \;\left[ \begin{array}{r} y_1 \\ y_2 \\ y_3 \end{array} \right] = \left[ \begin{array}{r} 6.0000 \\ -6.0000 \\ 6.0000 \end{array} \right]

obtemos a solução

(y_1, y_2, y_3) = (2.0000, -1.6222, 7.3054)

. Resolvendo agora o sistema triangular superior:

G^tx = y \Leftrightarrow \left[ \begin{array}{rrr} 3.0000 & -1.3333 & 0 \\ 0 & 2.0548 & -2.4333 \\ 0 & 0 & 0.2810 \end{array} \right] \;\left[ \begin{array}{r} x_1 \\ x_2 \\ x_3 \end{array} \right] = \left[ \begin{array}{r} 2.0000 \\ -1.6222 \\ 7.3054 \end{array} \right]

obtemos

(x_1, x_2, x_3) = (14, 30, 26)

. Esta é a solução de quadrados mínimos do sistema inicial.

Exemplo 2: considere o seguinte sistema linear na forma matricial:

Ax = b \Leftrightarrow \left[ \begin{array}{rrrr} 2 & -1 & 0 & 1 \\ 3 & 1 & 2 & 0 \\ -1 & 4 & 5 & 2 \\ 1 & 2 & 4 & 3 \\ 0 & 1 & 1 & -3 \end{array} \right] \; \left[ \begin{array}{r} x_1 \\ x_2 \\ x_3 \\ x_4 \end{array} \right] = \left[ \begin{array}{r} -1 \\ 0 \\ 1 \\ 2 \\ 1 \end{array} \right]

Queremos encontrar uma solução de quadrados mínimos deste sistema inconsistente. Temos que:

A^tA = \left[ \begin{array}{rrrrr} 2 & 3 & -1 & 1 & 0 \\ -1 & 1 & 4 & 2 & 1 \\ 0 & 2 & 5 & 4 & 1 \\ 1 & 0 & 2 & 3 & -3 \end{array} \right]\; \left[ \begin{array}{rrrr} 2 & -1 & 0 & 1 \\ 3 & 1 & 2 & 0 \\ -1 & 4 & 5 & 2 \\ 1 & 2 & 4 & 3 \\ 0 & 1 & 1 & -3 \end{array} \right] = \left[ \begin{array}{rrrr} 15 & -1 & 5 & 3 \\ -1 & 23 & 31 & 10 \\ 5 & 31 & 46 & 19 \\ 3 & 10 & 19 & 23 \end{array} \right]

O sistema normal associado ao sistema

Ax = b

é dado por:

A^tAx = A^tb \Leftrightarrow \left[ \begin{array}{rrrr} 15 & -1 & 5 & 3 \\ -1 & 23 & 31 & 10 \\ 5 & 31 & 46 & 19 \\ 3 & 10 & 19 & 23 \end{array} \right]\; \left[ \begin{array}{r} x_1 \\ x_2 \\ x_3 \\ x_4 \end{array} \right] = \left[ \begin{array}{r} -1 \\ 10 \\ 14 \\ 4 \end{array} \right]

A matriz

A^tA

é simétrica definida positiva e, utilizando uma precisão de 4 casas decimais, obtemos o fator de Cholesky:

G = \left[ \begin{array}{rrrr} 3.8730 & 0 & 0 & 0 \\ -0.2582 & 4.7889 & 0 & 0 \\ 1.2910 & 6.5429 & 1.2342 & 0 \\ 0.7746 & 2.1299 & 3.2928 & 2.6497 \end{array} \right]

tal que

A^tA = GG^t

. Assim, temos

A^tAx = A^tb \Leftrightarrow GG^tx = A^tb

. Resolvendo primeiro o sistema triangular inferior:

Gy = A^tb \Leftrightarrow \left[ \begin{array}{rrrr} 3.8730 & 0 & 0 & 0 \\ -0.2582 & 4.7889 & 0 & 0 \\ 1.2910 & 6.5429 & 1.2342 & 0 \\ 0.7746 & 2.1299 & 3.2928 & 2.6497 \end{array} \right] \;\left[ \begin{array}{r} y_1 \\ y_2 \\ y_3 \\ y_4 \end{array} \right] = \left[ \begin{array}{r} -1.0000 \\ 10.0000 \\ 14.0000 \\ 4.0000 \end{array} \right]

obtemos

(y_1, y_2, y_3, y_4) = (-0.2582, 2.0743, 0.6171, -0.8491)

. Resolvendo agora o sistema triangular superior:

G^tx = y \Leftrightarrow \left[ \begin{array}{rrrr} 3.8730 & -0.2582 & 1.2910 & 0.7746 \\ 0 & 4.7889 & 6.5429 & 2.1299 \\ 0 & 0 & 1.2342 & 3.2928 \\ 0 & 0 & 0 & 2.6497 \end{array} \right] \; \left[ \begin{array}{r} x_1 \\ x_2 \\ x_3 \\ x_4 \end{array} \right] = \left[ \begin{array}{r} -0.2582 \\ 2.0743 \\ 0.6171 \\ -0.8491 \end{array} \right]

obtemos a solução aproximada

(x_1, x_2, x_3, x_4) = (-0.5393, -1.2756, 1.3550, -0.3205)

. Esta é a solução de quadrados mínimos do sistema inicial.

Voltar ao Topo.

Utilizando a Fatoração Ortogonal

Considere um sistema linear

Ax = b

, com

m

equações e

n

incógnitas. Nosso problema é encontrar um elemento

x \in \mathbb{R}^n

tal que o vetor resíduo

r = Ax - b

que resulta da aproximação

x

como solução do sistema seja o menor possível, ou seja, que

\left\| r \right\|_2 = \left\| Ax - b \right\|_2

seja mínima. Seja

Q \in \mathbb{R}^m \times \mathbb{R}^m

uma matriz ortogonal qualquer e considere o seguinte sistema linear:

Q^tAx = Q^tb

Seja

s

o vetor resíduo resultante da aproximação

x

como solução deste novo sistema. Então:

s = Q^tAx - Q^tb = Q^t(Ax - b) = Q^tr

Como

Q^t

é uma matriz ortogonal, ela preserva norma e, portanto,

\left\| s \right\|_2 = \left\| Q^tr \right\|_2 = \left\| r \right\|_2

. Desta forma, um elemento

\bar{x} \in \mathbb{R}^n

que minimiza

\left\| r \right\|_2

também minimiza

\left\| s \right\|_2

, isto é, os dois sistemas possuem as mesmas soluções de quadrados mínimos. Nos interessa encontrar uma matriz ortogonal

Q

para a qual o sistema

Q^tAx = Q^tb

seja de fácil resolução.

Dada uma matriz

A \in \mathbb{R}^m \times \mathbb{R}^n

, sabemos que existe a fatoração ortogonal

A = QR

, onde

Q

é ortogonal e

R

é triangular superior. No caso em que

m > n

, então existe

Q \in \mathbb{R}^m \times \mathbb{R}^m

R \in \mathbb{R}^m \times \mathbb{R}^n

tais que

Q

é ortogonal e

R

é uma matriz em blocos na forma:

R = \left[\begin{array}{c} \hat{R} \\ 0 \end{array} \right]

onde

\hat{R} \in \mathbb{R}^n \times \mathbb{R}^n

é triangular superior e

A = QR

.

Considere o sistema

Ax = b

com

m

equações e

n

incógnitas, onde

m > n

. Usando a fatoração

A = QR \Leftrightarrow Q^tA = R

obtemos um novo sistema da forma:

Q^tAx = Q^tb \Leftrightarrow Rx = c

onde

c = Q^tb

. Escrevendo o vetor

c

em blocos da forma:

c = \left[\begin{array}{c} \hat{c} \\ d \end{array} \right]

onde

\hat{c} \in \mathbb{R}^n

, podemos expressar o vetor resíduo

s = Rx - c

, que resulta da aproximação

x

como solução do sistema

Rx = c

, da seguinte forma:

s = \left[\begin{array}{c} \hat{R} \\ 0 \end{array} \right] \; x - \left[\begin{array}{c} \hat{c} \\ d \end{array} \right] = \left[\begin{array}{c} \hat{R}x - \hat{c} \\ d \end{array} \right]

Assim,

\left\| s \right\|_2^2 = s_1^2 + ... + s_m^2 = \left\| \hat{R}x - \hat{c} \right\|_2^2 + \left\| d \right\|_2^2

Como o termo

\left\| d \right\|_2^2

independe de x,

\left\| s \right\|_2^2

é mínima quando

\left\| \hat{R}x - \hat{c} \right\|_2^2

é mínima. Logo, uma solução do sistema linear

\hat{R}x = \hat{c}

minimiza

\left\| s \right\|_2^2

, ou seja, é uma solução de quadrados mínimos do sistema

Rx = c

e também do sistema

Ax = b

.

Caso A tenha posto completo: neste caso temos que

posto(A) = n

, uma vez que

m > n

. Ao ser triangularizada, a matriz

A

produz a matriz

R

triangular superior

m \times n

, com

r_{ii} \neq 0

para

i = 1,...,n

. Desta matriz extraímos a matriz

\hat{R}

de ordem

n \times n

triangular superior, com

r_{ii} \neq 0

para

i = 1,...,n

, ou seja,

det(\hat{R}) \neq 0

. Assim, a matriz

\hat{R}

é inversível e, portanto, o sistema linear

\hat{R}x = \hat{c}

tem uma solução única, que também é a única solução de quadrados mínimos do sistema original

Ax = b

, e teremos

\left\|\hat{R}x - \hat{c}\right\|_2^2 = 0

, o que implica

\left\| s \right\|_2^2 = \left\| d \right\|_2^2

.

Caso A não tenha posto completo: considere

posto(A) = r

, onde

r < n

. Neste caso, ao obtermos a fatoração ortogonal de

A

, a triangularização de

A

terá apenas

r

linhas linearmente independentes, ou seja, a matriz

R

continua sendo triangular superior

m \times n

, mas com apenas

r

linhas não nulas. Assim, extraímos a matriz

\hat{R}

que é triangular superior de ordem

r \times n

, com

r < n

. Logo, o sistema

\hat{R}x = \hat{c}

possui mais incógnitas do que equações, ou seja, é indeterminado e admite infinitas soluções, pois algumas incógnitas são livres. E, para qualquer solução do sistema

\hat{R}x = \hat{c}

teremos

\left\|\hat{R}x-\hat{c}\right\|_2^2 = 0

. Portanto, o sistema linear

Ax = b

possui infinitas soluções de quadrados mínimos, mas para todas elas temos que

\left\|s\right\|_2^2 = \left\|d\right\|_2^2

.

Exemplo 3: considere o seguinte sistema linear inconsistente:

Ax = b \Leftrightarrow \left[ \begin{array}{rr} 1 & 3 \\ 2 & -1 \\ 2 & 2 \end{array}\right] \; \left[ \begin{array}{r} x_1 \\ x_2 \end{array}\right] = \left[ \begin{array}{r} 4 \\ 3 \\ 2 \end{array}\right]

Vamos determinar uma solução de quadrados mínimos através da fatoração ortogonal. Utilizando uma precisão de 4 casas decimais, obtemos a fatoração:

A = QR = \left[ \begin{array}{rrr} -0.3333 & 0.7297 & -0.5970 \\ -0.6667 & -0.6302 & -0.3980 \\ -0.6667 & 0.2653 & 0.6965 \end{array}\right] \;\left[ \begin{array}{rr} -3.0000 & -1.6667 \\ 0 & 3.3500 \\ 0 & 0 \end{array}\right]

onde

Q

é ortogonal. Da matriz

R

extraímos a matriz

2 \times 2

triangular superior:

\hat{R} = \left[ \begin{array}{rr} -3.0000 & -1.6667 \\ 0 & 3.3500 \end{array}\right]

Temos que

Q^tAx = Q^tb \Leftrightarrow Rx = c

, onde:

c = Q^tb = \left[ \begin{array}{rrr} -0.3333 & -0.6667 & -0.6667 \\ 0.7297 & -0.6302 & 0.2653 \\ -0.5970 & -0.3980 & 0.6965 \end{array}\right] \; \left[ \begin{array}{r} 4 \\ 3 \\ 2 \end{array}\right] = \left[ \begin{array}{r} -4.6667 \\ 1.5589 \\ -2.1891 \end{array}\right]

Queremos obter

x

de modo a minimizar a norma do resíduo:

Rx - c = \left[ \begin{array}{rr} -3.0000 & -1.6667 \\ 0 & 3.3500 \\ 0 & 0 \end{array}\right] \; \left[ \begin{array}{r} x_1 \\ x_2 \end{array}\right] - \left[ \begin{array}{r} -4.6667 \\ 1.5589 \\ -2.1891 \end{array}\right]

Do vetor

c

extraímos o vetor do

\mathbb{R}^2

\hat{c} = \left[ \begin{array}{r} -4.6667 \\ 1.5589 \end{array}\right]

Assim, obtemos o sistema triangular superior:

\hat{R}x = \hat{c} \Leftrightarrow \left[ \begin{array}{rr} -3.0000 & -1.6667 \\ 0 & 3.3500 \end{array}\right]\; \left[ \begin{array}{r} x_1 \\ x_2 \end{array}\right] = \left[ \begin{array}{r} -4.6667 \\ 1.5589 \end{array}\right]

cuja solução

(x_1, x_2) = (1.2970, 0.4653)

é também a solução de quadrados mínimos do sistema inicial. Como esta é uma solução exata do sistema

\hat{R}x = \hat{c}

, temos que

\left\|\hat{R}x - \hat{c} \right\|_2^2 = 0

e, portanto, a soma dos quadrados dos resíduos de

s = Rx-c

é dada apenas pela parte do vetor

c

que sobrou ao extrairmos o vetor

\hat{c}

, ou seja:

\left\| s \right\|_2^2 = \left\| (-2.1891) \right\|_2^2 \approx 4.7922

que é igual a norma do resíduo

r = Ax-b

.

Exemplo 4: considere o seguinte sistema linear:

Ax = b \Leftrightarrow \left[ \begin{array}{rrr} 3 & 1 & -1 \\ 1 & 2 & 0 \\ 0 & 1 & 2 \\ 1 & 1 & -1 \end{array}\right] \; \left[ \begin{array}{r} x_1 \\ x_2 \\ x_3 \end{array}\right] = \left[ \begin{array}{r} -3 \\ -3 \\ 8 \\ 9 \end{array}\right]

Vamos determinar uma solução de quadrados mínimos utilizando a fatoração ortogonal da matriz

A

. Com uma precisão de 4 casas decimais, obtemos a decomposição:

A = QR = \left[ \begin{array}{rrrr} -0.9045 & 0.3296 & -0.2563 & -0.0864 \\ -0.3015 & -0.7534 & 0.2698 & -0.5183 \\ 0 & -0.5180 & -0.7825 & 0.3455 \\ -0.3015 & -0.2354 & 0.4992 & 0.7775 \end{array}\right]\; \left[ \begin{array}{rrr} -3.3166 & -1.8091 & 1.2060 \\ 0 & -1.9306 & -1.1301 \\ 0 & 0 & -1.8078 \\ 0 & 0 & 0 \end{array}\right]

onde

Q

é uma matriz ortogonal. Da matriz

R

extraímos a matriz

3\times3

triangular superior:

\hat{R} = \left[ \begin{array}{rrr} -3.3166 & -1.8091 & 1.2060 \\ 0 & -1.9306 & -1.1301 \\ 0 & 0 & -1.8078 \end{array}\right]

Temos que

Q^tAx = Q^tb \Leftrightarrow Rx = c

, onde:

c = Q^tb = \left[ \begin{array}{rrrr} -0.9045 & -0.3015 & 0 & -0.3015 \\ 0.3296 & -0.7534 & -0.5180 & -0.2354 \\ -0.2563 & 0.2698 & -0.7825 & 0.4992 \\ -0.0864 & -0.5183 & 0.3455 & 0.7775 \end{array}\right]\; \left[ \begin{array}{r} -3 \\ -3 \\ 8 \\ 9 \end{array}\right] = \left[ \begin{array}{r} 0.9045 \\ -4.9913 \\ -1.8078 \\ 11.5758 \\ \end{array}\right]

Queremos obter

x

de modo a minimizar a norma do resíduo:

Rx-c = \left[ \begin{array}{rrr} -3.3166 & -1.8091 & 1.2060 \\ 0 & -1.9306 & -1.1301 \\ 0 & 0 & -1.8078 \\ 0 & 0 & 0 \end{array}\right]\;\left[ \begin{array}{r} x_1 \\ x_2 \\ x_3 \end{array}\right] - \left[ \begin{array}{r} 0.9045 \\ -4.9913 \\ -1.8078 \\ 11.5758 \\ \end{array}\right]

Do vetor

c

extraímos o vetor do

\mathbb{R}^3

\hat{c} = \left[ \begin{array}{r} 0.9045 \\ -4.9913 \\ -1.8078 \end{array}\right]

Assim, obtemos o sistema triangular superior:

\hat{R}x = \hat{c} \Leftrightarrow \left[ \begin{array}{rrr} -3.3166 & -1.8091 & 1.2060 \\ 0 & -1.9306 & -1.1301 \\ 0 & 0 & -1.8078 \end{array}\right] \;\left[ \begin{array}{r} x_1 \\ x_2 \\ x_3 \end{array}\right] = \left[ \begin{array}{r} 0.9045 \\ -4.9913 \\ -1.8078 \end{array}\right]

Resolvendo este sistema, obtemos

(x_1, x_2, x_3) = (-1, 2, 1)

, que também é a solução de quadrados mínimos do sistema inicial

Ax = b

. Como esta é uma solução exata do sistema

\hat{R}x = \hat{c}

, temos que

\left\|\hat{R}x - \hat{c} \right\|_2^2 = 0

e, portanto, a soma dos quadrados dos resíduos de

s = Rx-c

é dada apenas pela parte do vetor

c

que sobrou ao extrairmos o vetor

\hat{c}

, ou seja:

\left\| s \right\|_2^2 = \left\| 11.5758 \right\|_2^2 \approx 133.9991

que é igual a norma do resíduo

r = Ax-b

.

Exemplo 5: considere agora um seguinte sistema linear para o qual a matriz

A

não tem posto completo:

Ax = b \Leftrightarrow \left[ \begin{array}{rrr} 3 & 1 & 2 \\ 1 & 2 & 4 \\ 0 & 1 & 2 \\ 1 & 1 & 2 \end{array}\right] \; \left[ \begin{array}{r} x_1 \\ x_2 \\ x_3 \end{array}\right] = \left[ \begin{array}{r} -3 \\ -3 \\ 8 \\ 9 \end{array}\right]

Neste caso,

posto(A) = 2

. Na fatoração ortogonal de

A

com uma precisão de 4 casas decimais, obtemos:

A = QR = \left[ \begin{array}{rrrr} -0.9045 & 0.3296 & 0.1811 & -0.2010 \\ -0.3015 & -0.7534 & -0.4893 & -0. \\ 0 & -0.5180 & 0.8514 & -0.0825 \\ -0.3015 & -0.2354 & -0.0538 & 0.9224 \end{array}\right] \; \left[ \begin{array}{rrr} -3.3166 & -1.8091 & -3.6181 \\ 0 & -1.9306 & -3.8612 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right]

onde

Q

é uma matriz ortogonal. Da matriz

R

extraímos a matriz

2\times3

triangular superior:

\hat{R} = \left[ \begin{array}{rrr} -3.3166 & -1.8091 & -3.6181 \\ 0 & -1.9306 & -3.8612 \end{array}\right]

Temos que

Q^tAx = Q^tb \Leftrightarrow Rx = c

, onde:

c = Q^tb = \left[ \begin{array}{rrrr} -0.9045 & -0.3015 & 0 & -0.3015 \\ 0.3296 & -0.7534 & -0.5180 & -0.2354 \\ 0.1811 & -0.4893 & 0.8514 & -0.0538 \\ -0.2010 & -0.3194 & -0.0825 & 0.9224 \end{array}\right]\; \left[ \begin{array}{r} -3 \\ -3 \\ 8 \\ 9 \end{array}\right] = \left[ \begin{array}{r} 0.9045 \\ -4.9913 \\ 7.2514 \\ 9.2025 \end{array}\right]

Queremos obter

x

de modo a minimizar a norma do resíduo:

Rx-c = \left[ \begin{array}{rrr} -3.3166 & -1.8091 & -3.6181 \\ 0 & -1.9306 & -3.8612 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right]\; \left[ \begin{array}{r} x_1 \\ x_2 \\ x_3 \end{array}\right] - \left[ \begin{array}{r} 0.9045 \\ -4.9913 \\ 7.2514 \\ 9.2025 \end{array}\right]

Do vetor

c

extraímos o vetor do

\mathbb{R}^2

\hat{c} = \left[ \begin{array}{r} 0.9045 \\ -4.9913 \end{array}\right]

Assim, obtemos o sistema triangular superior:

\hat{R}x = \hat{c} \Leftrightarrow \left[ \begin{array}{rrr} -3.3166 & -1.8091 & -3.6181 \\ 0 & -1.9306 & -3.8612 \end{array}\right]\; \left[ \begin{array}{r} x_1 \\ x_2 \\ x_3 \end{array}\right] = \left[ \begin{array}{r} 0.9045 \\ -4.9913 \end{array}\right] \Leftrightarrow

\Leftrightarrow \left\lbrace \begin{array}{rrrrr} -3.3166 x_1 & -1.8091 x_2 & -3.6181 x_3 & = & 0.9045\\ & - 1.9306 x_2 & -3.8612 x_3 & = & -4.9913 \end{array} \right.

Note que este sistema é indeterminado. Escrevendo

x_2

em função de

x_3

na segunda equação, temos:

x_2 = -2x_3 + 2.5854

. Substituíndo na primeira equação e isolando

x_1

, obtemos:

x_1 = -1.6830

. Assim, o sistema original possui infinitas soluções de quadrados mínimos e representamos o conjunto solução por:

S = \left\lbrace x \in \mathbb{R}^3 \mid x = (-1.6830, 2.5854, 0) + \alpha (0, -2, 1), \;\; para \;qualquer \;\alpha \in \mathbb{R}\right\rbrace

E, para qualquer vetor

x

S

, teremos

\left\|\hat{R}x - \hat{c}\right\|_2^2 = 0

. Assim, a soma dos quadrados dos resíduos de

s = Rx-c

é dada apenas pela parte do vetor

c

que sobrou ao extrairmos o vetor

\hat{c}

, ou seja:

\left\|s\right\|_2^2 = 7.2514^2 + 9.2025^2 \approx 137.2688

que é igual a norma do resíduo

r = Ax-b

.

Voltar ao Topo.

Última Atualização: 03/08/2016.