Sistemas Lineares

Um dos principais problemas da Álgebra Linear e que surge nas mais diversas áreas é a resolução de sistemas de equações lineares. Um sistema linear com

m

equações e

n

incógnitas é normalmente escrito da forma:

\left\lbrace \begin{array}{ccccccccc} a_{11}x_1 & + & a_{12}x_2 & + & \cdots & + & a_{1n}x_n & = & b_1\\ a_{21}x_1 & + & a_{22}x_2 & + & \cdots & + & a_{2n}x_n & = & b_2\\ \vdots & & \vdots & & & & \vdots & & \vdots\\ a_{m1}x_1 & + & a_{m2}x_2 & + & \cdots & + & a_{mn}x_n & = & b_m\\ \end{array}\right.

onde

a_{ij}

, com

i = 1,...,m, j = 1,...,n

são os coeficientes do sistema linear,

x_j

, com

j = 1, ...,n

são as incógnitas, e

b_i

, com

i = 1,...,m

são as constantes.

Utilizando notação matricial, podemos representar o sistema linear da forma:

Ax = b

onde:

A = \left[ \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array}\right]

é a matriz dos coeficientes,

x = \left[ \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right], \;\;\;\;\;\;\;\;\;\;\;\; b = \left[ \begin{array}{c} b_1 \\ b_2 \\ \vdots \\ b_m \end{array} \right]

são o vetor das incógnitas e o vetor constante, respectivamente. A resolução do sistema linear consiste em encontrar uma

n

-upla

(x_1, x_2, ..., x_n)

, se existir, que satisfaça as

m

equações simultaneamente. O conjunto de todas as soluções do sistema linear é denominado conjunto solução do sistema.

Exemplo 1: Vamos começar com um sistema linear simples, com mesmo número de equações e incógnitas, ou seja,

n

equações e

n

incógnitas. Por exemplo, para

n = 2

considere o seguinte sistema linear:

\left\lbrace \begin{array}{r} 1x + 2y = 3 \\ 3x + 5y = 7 \end{array} \right.

Nesse caso, as incógnitas são

x

y

. Uma maneira simples para resolver esse sistema é através da eliminação:

1) Subtraindo 3 vezes a primeira equação da segunda equação, eliminamos a incógnita

x

da segunda equação e ficamos com uma equação linear somente em

y

(equação\; 2) - 3\;(equação\; 1) \Rightarrow 0x -y = -2

De onde obtemos

y = 2

.

2) Agora, basta substituir o valor encontrado de

y

na primeira equação, por exemplo:

1x + 2y = 3 \Rightarrow 1x + 2(2) = 3 \Rightarrow x = 3-4 \Rightarrow x = -1

Assim, encontramos um par

(x,y) = (-1,2)

que satisfaz ambas as equações.

Esse exemplo é bem simples e conseguimos resolvê-lo à mão. Mas, em problemas reais, que dependem da resolução de sistemas lineares com n equações e

n

incógnitas, onde n é muito grande, (

n= 1000

, por exemplo) seria inviável resolver à mão, ainda mais sem um bom método para sua resolução, pois os cálculos envolveriam milhões de coeficientes das equações, acabaríamos nos perdendo e as chances de erros seriam muito grandes.

Um método para a resolução de sistemas lineares é o método de Cramer. Mas, para um sistema

n \times n

, este requer o cálculo de

n+1

determinantes de matrizes

n \times n

, e cada determinante requer em torno de

n!

operações. Para

n = 20

, por exemplo, o cálculo envolveria aproximadamente

20!*21 \approx 5.1*10^{19}

operações. Considerando um computador que realiza

2000000

(dois milhões) de operações por segundo, levaria, aproximadamente,

810042

anos para resolver este sistema, o que é inviável.

Observe que no caso de um sistema linear

n \times n

que possui solução única, o vetor solução

x

é dado por

x = A^{-1}b

. Porém, calcular a matriz inversa

A^{-1}

é desaconselhável, pois envolve muitas operações, o que torna esse processo não competitivo com os demais métodos utilizados na resolução de sistemas lineares.

Voltar ao Topo.

Interpretação Geométrica por Linhas e Colunas

Considere um sistema linear, com 2 equações e 2 incógnitas, por exemplo:

\left\lbrace \begin{array}{r} 1x + 2y = 5 \\ 3x - 1y = 1 \end{array} \right.

Esse sistema possui única solução

x = 1

y = 2

. Vamos analisar o sistema através das suas linhas e colunas.

Olhando para as linhas do sistema, ou seja, para as equações separadamente, observe que a equação

1x + 2y = 5

é uma reta no plano

xy

que passa pelos pontos

(5,0)

(1,2)

, por exemplo. Do mesmo modo, a segunda equação

3x - y = 1

é uma outra reta, que intercepta a primeira no ponto

(1,2)

; este ponto de intersecção pertence a ambas as retas e é a única solução para as duas equações (Figura 1(a)).

Se considerarmos agora as colunas do sistema, podemos escrevê-lo da forma:

x\;\left[ \begin{array}{c} 1 \\ 3 \end{array} \right] + y \;\left[ \begin{array}{r} 2 \\ -1 \end{array} \right] = \left[ \begin{array}{c} 5 \\ 1 \end{array} \right]

Do ponto de vista das colunas, o problema de resolver o sistema linear é equivalente ao de encontrar a combinação linear dos vetores

(1,3)

(2,-1)

que resulta no vetor

(5,1)

. A ideia geométrica da solução é que o vetor

(1,3)

multiplicado por 1 somado com o vetor

(2,-1)

multiplicado por 2 nos dá o vetor

(5,1)

e esta é a única combinação possível (Figura 1(b)).

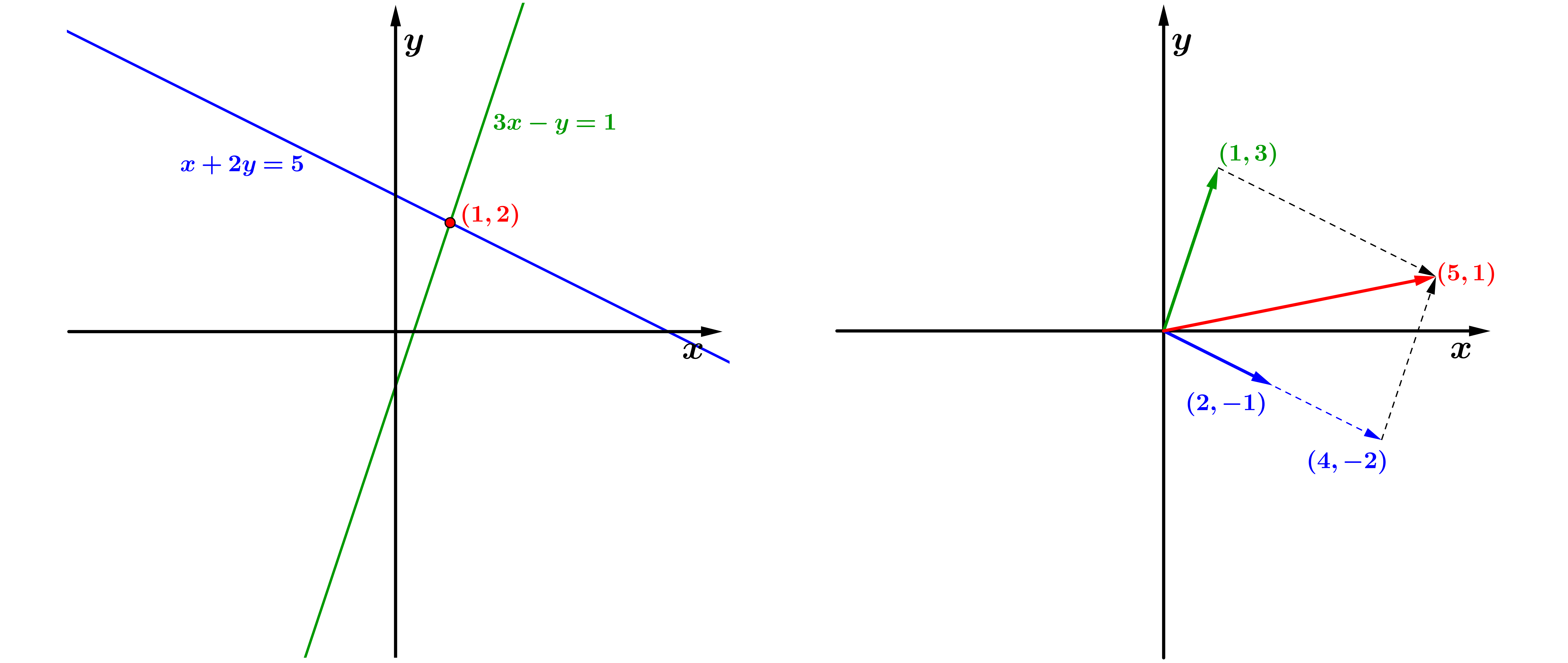
(a) Interpretação por linhas. (b) Interpretação por colunas.

Mas, nem todos os sistemas lineares têm solução e alguns têm infinitas soluções. Considere agora, por exemplo, o seguinte sistema:

\left\lbrace \begin{array}{r} 1x + 2y = 5 \\ 3x + 6y = 1 \end{array} \right.

Se tentarmos utilizar a eliminação para esse sistema, subtraindo 3 vezes a primeira equação da segunda equação, obtemos:

(equação\; 2) - 3\;(equação\; 1) \Rightarrow 0x + 0y = -14

O que não é possível. Isso mostra que não existe um par

(x,y)

que resolve as duas equações simultaneamente, ou seja, o sistema linear não possui solução.

Geometricamente, olhando para as linhas do sistema, as equações

x + 2y = 5

3x + 6y = 1

representam retas que são paralelas e que, portanto, não se interceptam (Figura 2(a)).

Olhando agora o sistema pelas suas colunas, observe que, escrevendo o sistema da forma:

x\; \left[ \begin{array}{c} 1 \\ 3 \end{array} \right] + y\; \left[ \begin{array}{r} 2 \\ 6 \end{array} \right] = \left[ \begin{array}{c} 5 \\ 1 \end{array} \right]

temos uma combinação linear dos vetores

(1,3)

(2,6)

resultando no vetor

(5, 1)

, o que é impossível, uma vez que os vetores

(1,3)

(2,6)

são paralelos, ou seja, estão na mesma direção, e o vetor

(5,1)

está em outra. Assim, não existem valores

x

y

que satisfaçam essa combinação linear (Figura 2(b)).

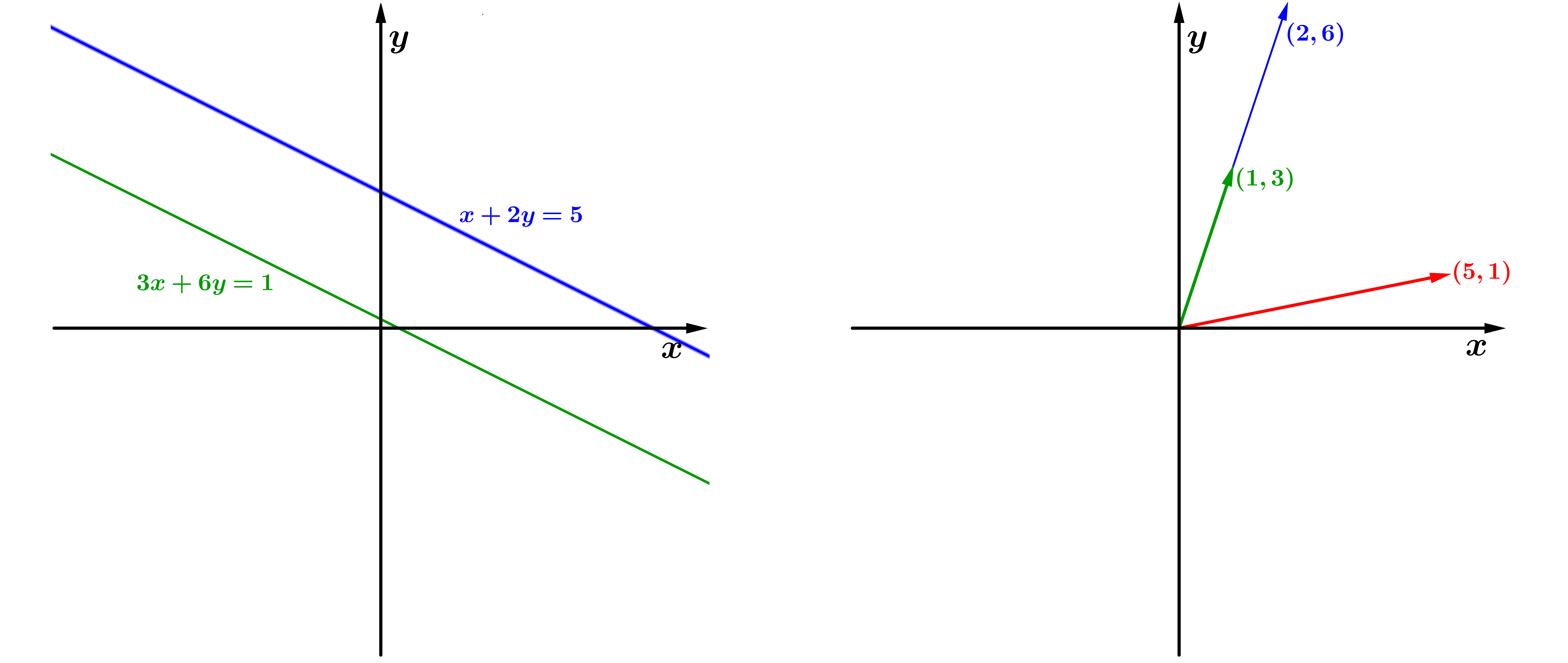
(a) Interpretação por linhas. (b) Interpretação por colunas.

Se considerarmos agora, por exemplo, o seguinte sistema linear:

\left\lbrace \begin{array}{l} 1x + 2y = 5 \\ 3x + 6y = 15 \end{array} \right.

Realizando a mesma eliminação anterior, obtemos:

(equação\; 2) - 3\;(equação\; 1) \Rightarrow 0x + 0y = 0

e assim uma das equações se anula e qualquer valor

(x,y)

a satisfaz. Dessa forma, o sistema linear admite infinitas soluções.

Olhando as linhas do sistema, observe que a equação

3x + 6y = 15

é 3 vezes a equação

1x + 2y = 5

, ou seja, uma equação é múltipla da outra. Portanto, as equações do sistema são linearmente dependentes e, geometricamente, elas representam a mesma reta. Dessa forma, todos os pontos

(x,y)

que satisfazem a equação 1 também satisfazem a equação 2, portanto, o sistema linear possui infinitas soluções (Figura 3(a)).

Considerando as colunas do sistema e escrevendo-o da forma:

x\;\left[ \begin{array}{c} 1 \\ 3 \end{array} \right] + y\;\left[ \begin{array}{r} 2 \\ 6 \end{array} \right] = \left[ \begin{array}{c} 5 \\ 15 \end{array} \right]

obtemos uma combinação linear dos vetores

(1,3)

(2,6)

que resulta no vetor

(1,15)

. Mas, esses vetores estão todos na mesma direção, e portanto existem infinitos valores

x

y

que satisfazem a combinação linear (Figura 3(b)).

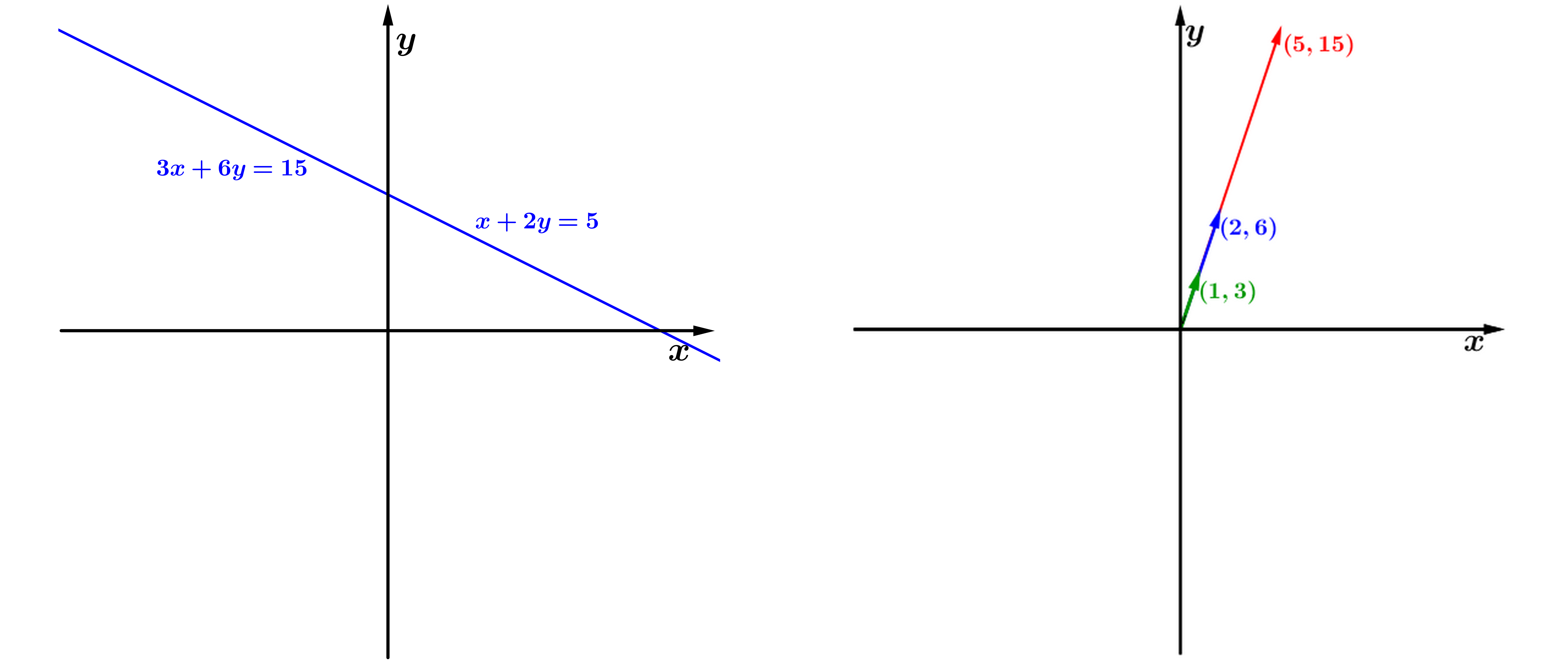
(a) Interpretação por linhas. (b) Interpretação por colunas.

Para um sistema linear com 3 equações e 3 incógnitas, note que cada equação representa um plano no espaço com 3 dimensões. Se esses 3 planos se interceptam em um ponto, essa é a única solução do sistema linear. Se eles não se interceptam o sistema não possui solução e, se eles se interceptam em uma reta ou são coincidentes, o sistema possui infinitas soluções.

Podemos aplicar o mesmo raciocínio para sistemas com

n

equações e

n

incógnitas, porém não é possível visualizar geometricamente as equações em um espaço

n

-dimensional, quando

n > 3

. Ainda assim, cada equação do sistema representará um ``plano'' com dimensão

n-1

. A intersecção entre dois desses planos será um conjunto de dimensão

n-2

. Se o sistema tiver única solução, cada equação reduzirá a dimensão da intersecção em 1 e no final, teremos um único ponto, ou seja, uma

n

-upla, cujas coordenadas satisfazem todas as equações do sistema.

De um modo geral, um sistema linear pode admitir apenas um dos três casos: uma única solução, nenhuma solução ou infinitas soluções.

Voltar ao Topo.

Última Atualização: 02/02/2016.