Operações Elementares

Definição: Dizemos que dois sistemas lineares são equivalentes quando eles possuem o mesmo conjunto solução.

Uma forma de resolver o sistema linear é substituí-lo por outro equivalente, mas que seja mais fácil de resolver. Esse novo sistema pode ser obtido aplicando-se uma série de operações sobre as equações do sistema, que não alterem sua solução.

Definição: Uma operação elementar sobre as linhas de uma matriz é uma das seguintes operações:

(i) Permutar duas linhas da matriz.
Notação:

l_i \longleftrightarrow l_j

(ii) Multiplicar uma linha por um escalar

\alpha \neq 0

.
Notação:

l_i \longleftarrow \alpha l_i

(iii) Somar à uma linha da matriz outra multiplicada por um escalar

\alpha \neq 0

.
Notação:

l_i \longleftarrow l_i + \alpha l_j

De modo análogo, podemos definir operações elementares sobre as colunas de uma matriz.

Considere um sistema linear escrito na forma matricial

Ax = b

. Note que, se trocarmos o termo ``linha da matriz'' por ``equação do sistema'' na definição anterior, teremos operações elementares que podem ser aplicadas sobre as equações de um sistema linear. Mas, quando realizamos essas operações sobre o sistema, apenas os coeficientes

a_{ij}

e os termos

b_i

são alterados, e não as incógnitas. Assim, para aplicarmos operações elementares sobre um sistema linear, basta aplicarmos essas operações sobre a seguinte matriz, denominada matriz ampliada do sistema:

\left[\begin{array}{c|c} A & b \end{array} \right] = \left[ \begin{array}{cccc|c} a_{11} & a_{12} & \cdots & a_{1n} & b_1 \\ a_{21} & a_{22} & \cdots & a_{2n} & b_2 \\ \vdots & \vdots & & \vdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} & b_m \end{array}\right]

Teorema 1: Sejam

Ax = b

Cx = d

dois sistemas lineares. Se o segundo sistema é obtido aplicando-se uma sequência de operações elementares sobre as equações do outro, ou seja, se a matriz ampliada

\left[\begin{array}{c|c} C & d \end{array} \right]

é obtida aplicando-se uma sequência de operações elementares sobre as linhas da matriz

\left[\begin{array}{c|c} A & b \end{array} \right]

, então os dois sistemas são equivalentes.

Demonstração: AQUI.

Esse teorema garante que ao aplicarmos uma série de operações elementares sobre as equações de um sistema linear, obtemos um novo sistema equivalente, que pode ser mais fácil de resolver.

Exemplo 1: Considere o seguinte sistema linear:

\left\lbrace \begin{array}{rrrrr} 1x & + & 2y & = & 5 \\ 3x & - & 1y & = & 1 \end{array} \right.

Aplicando as operações elementares

l_2 \longleftarrow l_2 - 3 l_1

l_2 \longleftarrow -\frac{1}{7}l_2

, nesta ordem, sobre as linhas da matriz ampliada do sistema, obtemos:

\left[ \begin{array}{rr|r} 1 & 2 & 5 \\ 3 & -1 & 1 \end{array}\right] \longrightarrow \left[ \begin{array}{rr|r} 1 & 2 & 5 \\ 0 & -7 & -14 \end{array}\right] \longrightarrow \left[\begin{array}{rr|r} 1 & 2 & 5 \\ 0 & 1 & 2 \end{array}\right]

Temos um novo sistema linear equivalente ao inicial, ou seja, com o mesmo conjunto solução:

\left\lbrace \begin{array}{rrrrr} 1x & + & 2y & = & 5 \\ 0x & + & 1y & = & 2 \end{array} \right.

Ao aplicarmos a operação elementar

l_2 \longleftarrow l_2 - 3 l_1

sobre as equações do sistema, a equação

x + 2y = 5

se mantem e a equação

3x - y = 1

se torna a equação

y = 2

. Geometricamente, a reta

3x - y = 1

é rotacionada em torno do ponto

(1,2)

, que é a solução do sistema, até a reta

y = 2

. Aplicando a operação

l_2 \longleftarrow -\frac{1}{7}l_2

as equações se mantém, uma vez que

-7y = -4

é equivalente a

y = 2

e aplicamos esta operação elementar apenas para facilitar os cálculos e a interpretação geométrica.

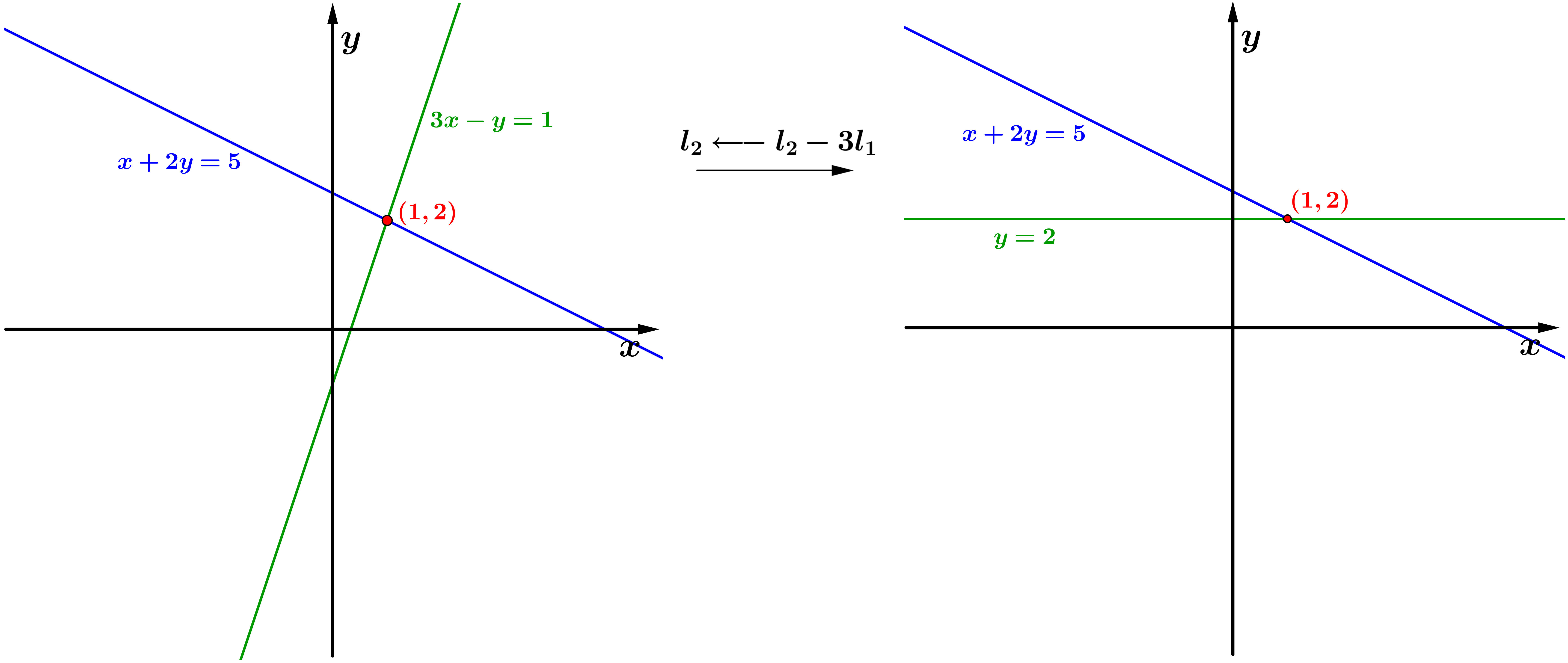
Figura 1: Aplicando a operação elementar

l_2 \longleftarrow l_2 - 3 l_1

sobre as equações do sistema.

Se continuarmos a eliminação, aplicando a operação elementar

l_1 \longleftarrow l_1 - 2 l_2

na matriz ampliada desse novo sistema, obtemos:

\left[ \begin{array}{rr|r} 1 & 2 & 5 \\ 0 & 1 & 2 \end{array}\right] \longrightarrow \left[ \begin{array}{rr|r} 1 & 0 & 1 \\ 0 & 1 & 2 \end{array}\right]

Temos então um novo sistema linear equivalente ao anterior e também equivalente ao inicial:

\left\lbrace \begin{array}{rrrrr} 1x & + & 0y & = & 1 \\ 0x & + & 1y & = & 2 \end{array} \right.

esse novo sistema tem única solução trivial

x = 1

y=2

, que também é solução para o sistema linear inicial. Ao aplicarmos a operação elementar

l_1 \longleftarrow l_1 - 2 l_2

sobre as equações do sistema, a equação

y = 2

se mantem e a equação

x + 2y = 5

se torna a equação

x = 1

. Geometricamente, a reta

x + 2y = 5

é rotacionada em torno do ponto

(1,2)

até a reta

x = 1

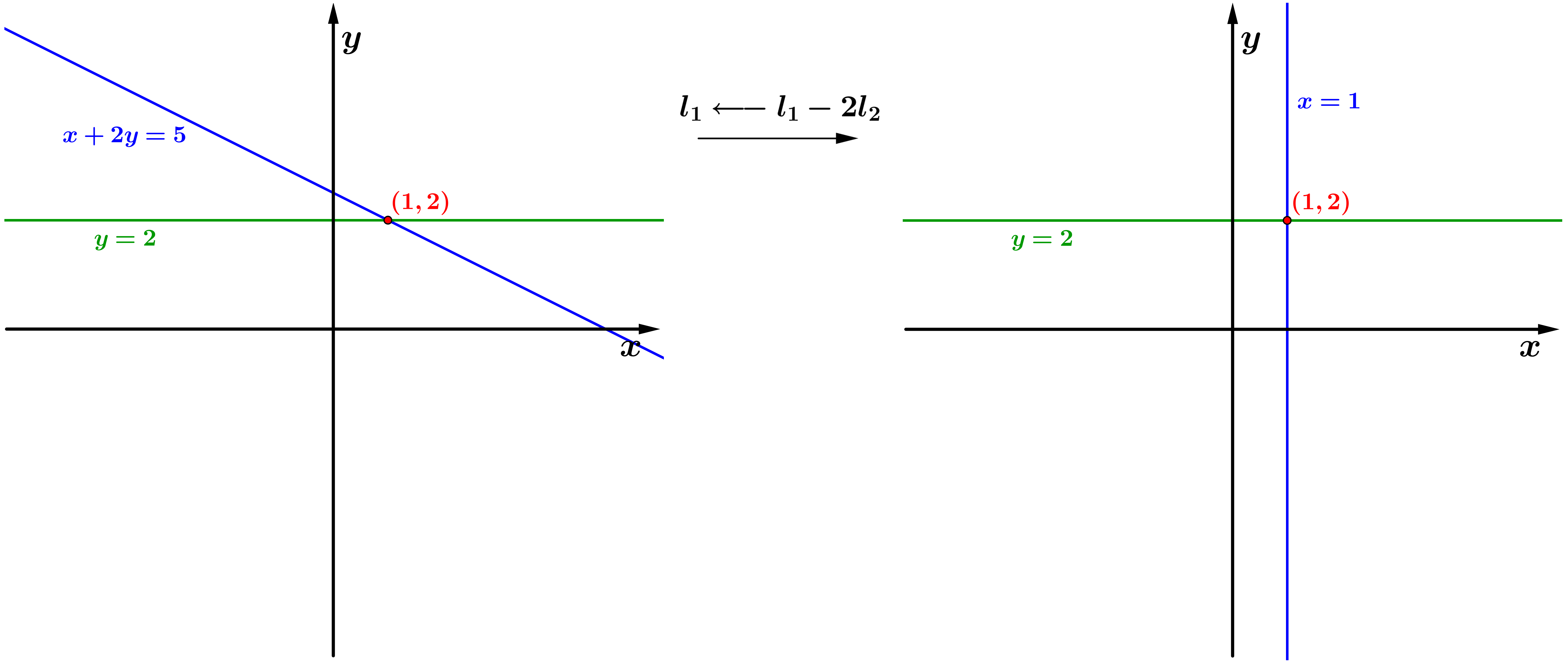
Figura 2: Aplicando a operação elementar

l_1 \longleftarrow l_1 - 2 l_2

sobre as equações do sistema.

Encontrar a intersecção das retas

x = 1

y = 2

é bem mais simples, que claramente é o ponto

(1,2)

. E essa é a solução do sistema linear inicial, pois apenas aplicamos uma sequência de operações elementares sobre as equações do sistema, o que garante que obtivemos sistemas equivalentes durante o processo.

Exemplo 2: Considere o seguinte sistema linear:

\left\lbrace \begin{array}{rrrrrrr} x & - & 2y & + & z & = & -1 \\ 2x & - & 3y & + & z & = & -3 \\ x & + & 4y & + & 2z & = & 7 \end{array}\right.

Aplicando a sequência de operações elementares:

l_2 \longleftarrow l_2 - 2l_1, \;\;\;\;\;\; l_3 \longleftarrow l_3 - l_1, \;\;\;\;\;\; l_3 \longleftarrow l_3 - 6 l_2

sobre as linhas da matriz ampliada do sistema, obtemos:

\left[ \begin{array}{rrr|r} 1 & -2 & 1 & -1 \\ 2 & -3 & 1 & -3 \\ 1 & 4 & 2 & 7 \end{array}\right] \longrightarrow \left[ \begin{array}{rrr|r} 1 & -2 & 1 & -1 \\ 0 & 1 & -1 & -1 \\ 1 & 4 & 2 & 7 \end{array}\right] \longrightarrow\left[ \begin{array}{rrr|r} 1 & -2 & 1 & -1 \\ 0 & 1 & -1 & -1 \\ 0 & 6 & 1 & 8 \end{array}\right] \longrightarrow

\longrightarrow \left[ \begin{array}{rrr|r} 1 & -2 & 1 & -1 \\ 0 & 1 & -1 & -1 \\ 0 & 0 & 7 & 14 \end{array}\right]

Temos então um novo sistema linear equivalente ao original, mas este sistema é de resolução direta, pois a matriz dos coeficientes é triangular superior:

\left\lbrace \begin{array}{rrrrrrr} x & - & 2y & + & z & = & -1 \\ 0x & + & y & - & z & = & -1 \\ 0x & + & 0y & + & 7z & = & 14 \end{array}\right.

Da última equação temos que

z = 2

. Substituíndo na segunda equação, obtemos:

y - 2 = -1 \Rightarrow y = 1

e substituíndo os valores de

y

z

na primeira equação, obtemos:

x - 2(1) + 2 = -1 \Rightarrow x = -1

Portanto, a única solução do novo sistema linear é

x = -1

y = 1

z = 2

e essa é também a única solução do sistema inicial, pois são equivalentes.

Voltar ao Topo.

Matrizes Elementares

Definição: A matriz

n \times n

obtida aplicando-se uma única operação elementar sobre a matriz identidade

I_n

, de ordem

n

, é denominada uma matriz elementar.

Exemplo 3: Considere a matriz identidade

I_3

.

(a) Aplicando a operação elementar

l_1 \longleftrightarrow l_2

à essa matriz, obtemos:

I_3 = \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right] \longrightarrow\left[\begin{array}{ccc} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{array} \right] = E

A matriz

E

é uma matriz elementar que representa a operação elementar: permutar a linha 1 com a linha 2.

(b) Aplicando a operação elementar

l_2 \longleftarrow \alpha l_2, \alpha \neq 0

, sobre a matriz

I_3

, temos:

I_3 = \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right] \longrightarrow \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \alpha & 0 \\ 0 & 0 & 1 \end{array} \right] = E

A matriz

E

é uma matriz elementar que representa a operação elementar: multiplicar a linha 2 por um escalar

\alpha

não nulo.

(c) Aplicando a operação elementar

l_3 \longleftarrow l_3 + \alpha l_1

\alpha \neq 0

, sobre a matriz

I_3

, temos:

I_3 = \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right] \longrightarrow \left[\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ \alpha & 0 & 1 \end{array} \right] = E

A matriz

E

é uma matriz elementar que representa a operação elementar: somar à linha 3 a linha 1 multiplicada por um escalar

\alpha

não nulo.

Teorema 2: Sejam

A

uma matriz

m \times n

E

uma matriz elementar,

m \times m

, que representa uma certa operação elementar de linhas. Então, a matriz

F = EA

é a matriz obtida quando esta mesma operação elementar é aplicada sobre as linhas de

A

.

Demonstração: AQUI.

Exemplo 4: Considere a matriz

A

dada por:

A = \left[\begin{array}{cc} 2 & 3 \\ 1 & 4 \end{array}\right]

e duas operações elementares de linha:

l_1 \longleftrightarrow l_2

l_2 \longleftarrow l_2 - 2l_1

. As matrizes elementares relacionadas a estas operações elementares, respectivamente, são:

E_1 = \left[ \begin{array}{rr} 0 & 1 \\ 1 & 0 \end{array}\right], \;\;\;\;\;\; \;\;\;\;\;\; E_2 = \left[ \begin{array}{rr} 1 & 0 \\ -2 & 1 \end{array}\right]

Aplicar a sequência de operações elementares:

l_1 \longleftrightarrow l_2

e depois

l_2 \longleftarrow l_2 - 2l_1

sobre a matriz

A

é o mesmo que multiplicar

A

pela esquerda por

E_1

e o resultado multiplicar novamente pela esquerda por

E_2

, ou seja,

E_2 \left( E_1 A \right) = \left[ \begin{array}{rr} 1 & 0 \\ -2 & 1 \end{array}\right] \;\left( \;\left[ \begin{array}{rr} 0 & 1 \\ 1 & 0 \end{array}\right] \left[ \begin{array}{rr} 2 & 3 \\ 1 & 4 \end{array}\right]\; \right) = \left[ \begin{array}{rr} 1 & 0 \\ -2 & 1 \end{array}\right] \;\left[ \begin{array}{rr} 1 & 4 \\ 2 & 3 \end{array}\right] = \left[ \begin{array}{rr} 1 & 4 \\ 0 & -5 \end{array}\right]

Definição: Uma operação elementar inversa é uma operação que desfaz o efeito de uma operação elementar, isto é, depois de aplicada uma determinada operação elementar sobre uma matriz, ao aplicar sobre a matriz resultante a operação elementar inversa recuperamos a matriz inicial. A cada operação elementar está associada uma operação elementar inversa.

Considere uma matriz

A

e uma operação elementar aplicada sobre as linhas de

A

. Então:

Se a operação elementar é: permutar as linhas $r$ e $s$ de $A$ . Então, para recuperarmos a matriz $A$ basta permutar novamente as linhas $r$ e $s$ , e esta é a operação elementar inversa.

Se a operação elementar é: multiplicar a linha $r$ de $A$ por um escalar $\alpha \neq 0$ . Então, para recuperarmos a matriz $A$ basta multiplicar a linha $r$ por $\frac{1}{\alpha}$ , e esta é a operação elementar inversa.

Se a operação elementar é: somar à linha $r$ outra linha $s$ multiplicada por um escalar $\alpha \neq 0$ . Então, para recuperarmos a matriz $A$ basta subtrair da linha $r$ a linha $s$ multiplicada pelo mesmo escalar $\alpha$ , ou seja, somar à linha $r$ a linha $s$ multiplicada por $-\alpha$ , e esta é a operação elementar inversa.

Teorema 3: Toda matriz elementar é invertível e a inversa é também uma matriz elementar.

Demonstração: AQUI.

Voltar ao Topo.

Última Atualização: 02/02/2016.