Definição
Seja um espaço vetorial sobre um corpo K. O elemento é uma Combinação Linear dos elementos se existem escalares , de modo que:Ou seja, o elemento pode ser escrito como a soma dos elementos multiplicados por escalares do corpo.
Exemplos
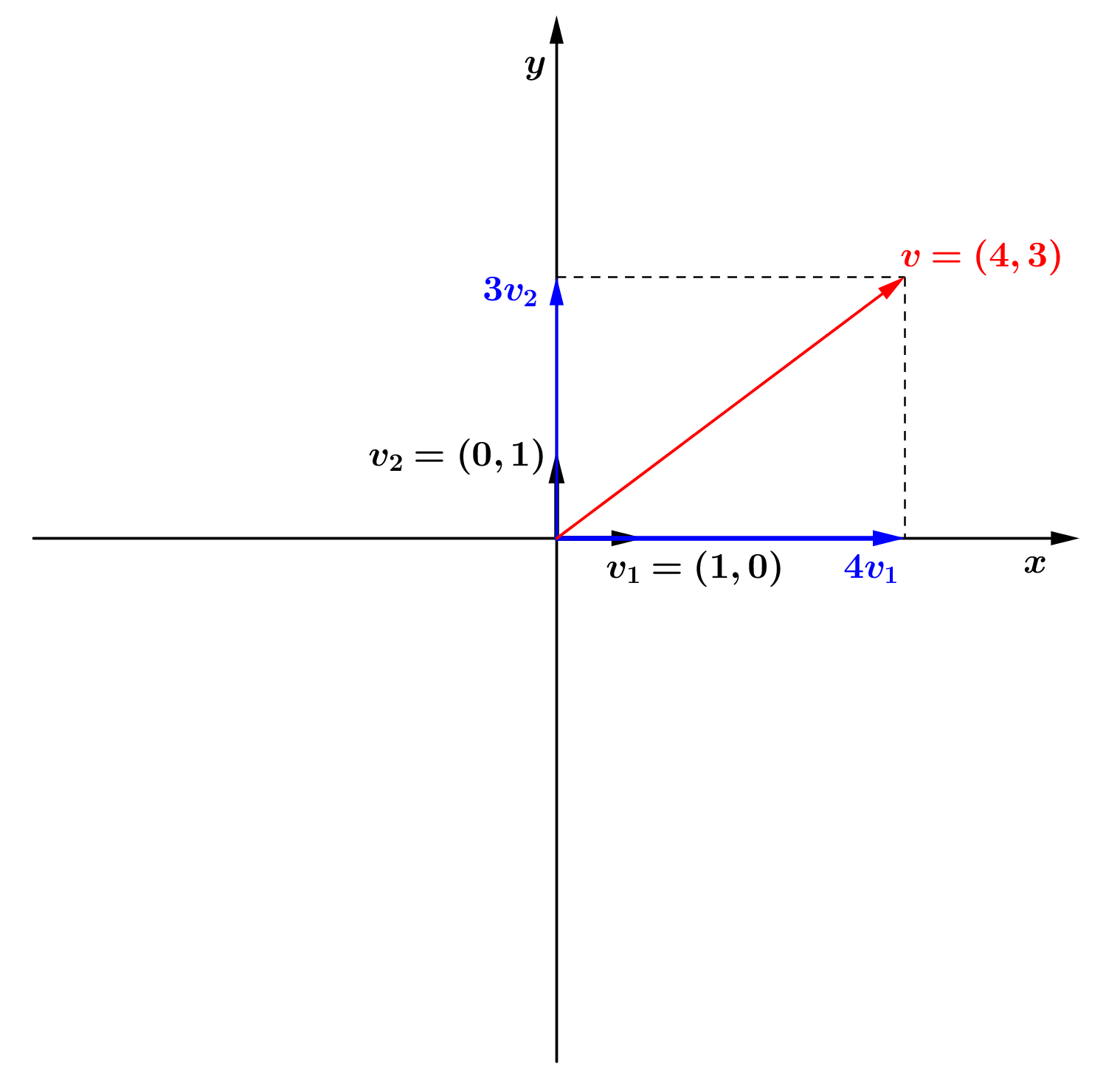
Exemplo 1: O
elemento
é combinação linear dos elementos
e .
De fato,
pode ser escrito como:
Assim, existem os escalares e tais que
pode ser escrito como . Logo, é combinação linear de
e
.
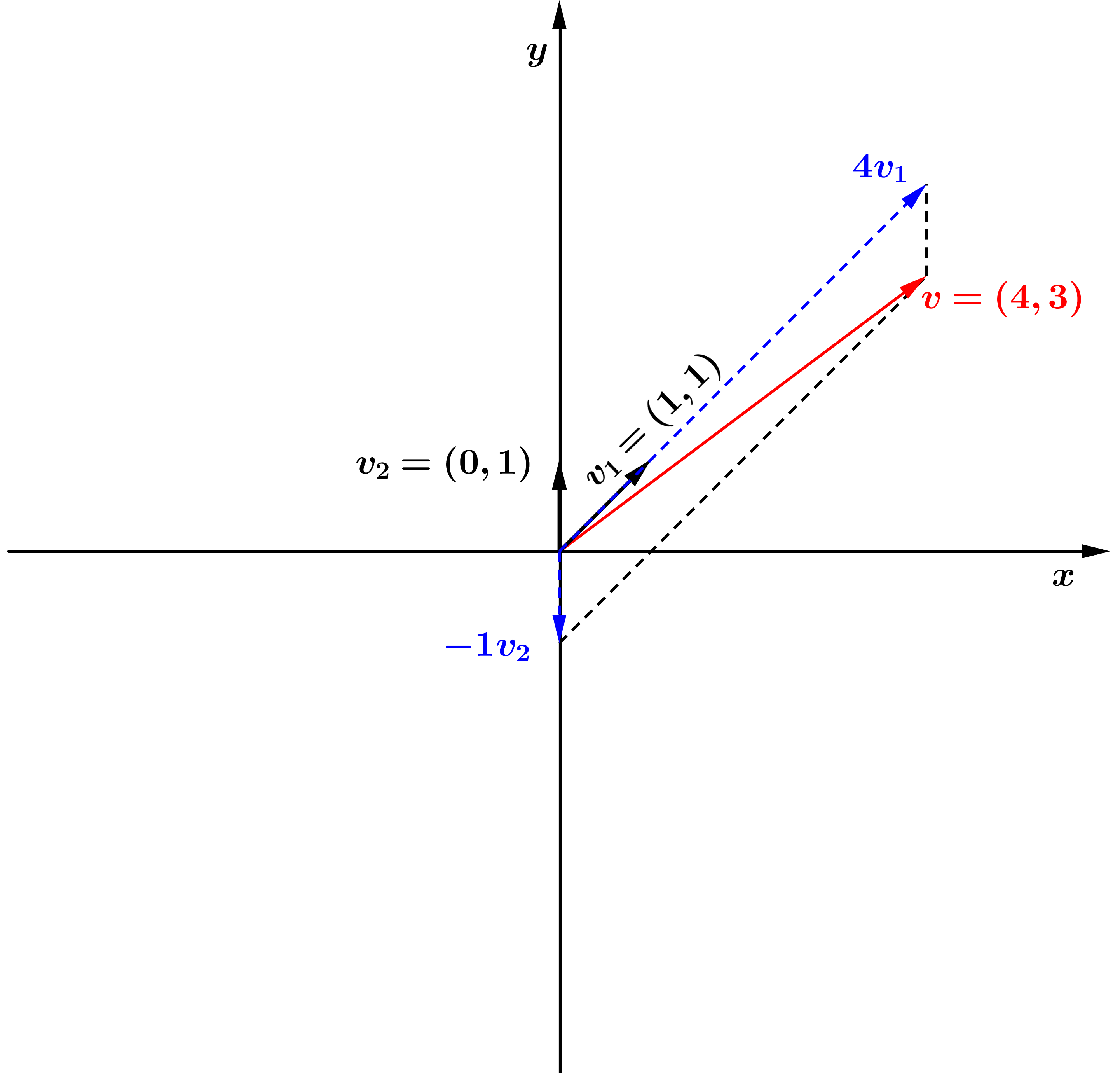
Exemplo 2: Considere
o mesmo vetor
do exemplo anterior, ele também pode ser escrito
como combinação linear dos vetores
e
da forma:
Exemplo 3: O
polinômio
pode ser escrito como combinação linear dos
polinômios
e .
Neste caso, basta tomar como constantes os coeficientes do polinômio , assim temos:
Logo,
é combinação linear dos polinômios
Para que
seja combinação linear de
é preciso que existam de
modo que:
Assim, .