Ajuste de Curvas
Página Inicial
ESPAÇOS VETORIAIS
Espaços Vetoriais
Subespaços Vetoriais
Combinação Linear
Subespaços Gerados
Intersecção de Subespaços
Soma de Subespaços
Dependência Linear
Base e Dimensão
Mudança de Base

TRANSFORMAÇÕES LINEARES
Transformações Lineares
Núcleo e Imagem
Teorema do Núcleo e da Imagem
Isomorfismo e Automorfismo
Álgebra das Transformações Lineares
Matriz de uma Transformação

AUTOVALORES E AUTOVETORES
Autovalores e Autovetores
Polinômio Característico
Diagonalização

ESPAÇOS COM PRODUTO INTERNO
Produto Interno
Norma e Distância
Ortogonalidade

DETERMINANTES
Determinantes
Propriedades do Determinante
Cálculo de Determinantes

SISTEMAS LINEARES
Sistemas Lineares
Operações Elementares
Sistemas Triangulares
Eliminação Gaussiana

FATORAÇÕES MATRICIAIS
Fatoração LU
Fatoração de Cholesky
Fatoração Ortogonal
Fatoração QR - Processo de Gram-Schmidt
Fatoração QR - Transformações de Householder

QUADRADOS MÍNIMOS
Método de Quadrados Mínimos
Ajuste de Curvas
Problemas Aplicados

 OUTRAS APLICAÇÕES
Curvas e Superfícies por Pontos Especificados
Criptografia
Jogos de Estratégia
Classificação de Cônicas


Um problema comum em experimentos científicos é o de obter uma relação matemática f(x)=yf(x) = y entre duas variáveis xx e yy, isto é, obter uma curva que se ajuste aos pontos correspondentes a um conjunto de dados obtidos experimentalmente:

(x1,y1),(x2,y2),...,(xm,ym)(x_1, y_1), (x_2, y_2), ..., (x_m,y_m)
Normalmente, temos alguma razão teórica para acreditar que estes pontos pertencem a uma mesma reta, parábola ou outro gráfico de função. Na prática, como os dados são obtidos experimentalmente, temos alguns erros de medição, o que torna impossível encontrarmos uma curva que se ajuste perfeitamente a todos os pontos. Assim, a ideia é escolher uma curva, determinando seus coeficientes, que melhor se ajusta aos dados.

Queremos obter uma função f:ℝ⟶ℝf: \mathbb{R} \longrightarrow\mathbb{R}, tal que:

f(xi)=yi,i=1,...,mf(x_i) = y_i,\;\;\;\;\;\;\;\;\;\;\;\; i = 1, ..., m
Como estas equações não podem ser satisfeitas simultaneamente, procuramos uma função f^\hat{f} que minimize os erros:

|f^(xi)-yi|,i=1,...,m\left|\hat{f}(x_i) - y_i\right|,\;\;\;\;\;\;\;\;\;\;\;\; i = 1, ..., m
Seja r=(r1,...,rm)tr = (r_1, ..., r_m)^t o vetor de resíduos ri=f^(xi)-yir_i = \hat{f}(x_i) - y_i. Nosso problema pode ser resolvido minimizando ‖r‖2\left\|r\right\|_2, que é o mesmo que minimizar:

‖r‖22=r12+...+rm2=(f^(x1)-y1)2+...+(f^(xm)-ym)2\left\|r\right\|_2^2 = r_1^2 + ... +r_m^2 = \left(\hat{f}(x_1) - y_1\right)^2 + ... +\left(\hat{f}(x_m) - y_m\right)^2
Este é denominado um problema de quadrados mínimos discreto, pois ajustamos uma curva a uma quantidade discreta (finita ou infinita enumerável) de dados. O caso contínuo, no qual buscamos ajustar uma curva a uma quantidade contínua de dados, não será estudado neste texto.

Caso Linear

Considerando que obtivemos uma tabela de pontos (x1,f(x1)),(x2,f(x2)),...,(xm,f(xm))(x_1, f(x_1)), (x_2, f(x_2)), ...,(x_m, f(x_m)), com x1,x2,...,xmx_1, x_2, ..., x_m pertencentes a um intervalo [a,b][a,b], o problema de ajuste de curvas consiste em escolher nn funções g1(x),g2(x),...,gn(x)g_1(x), g_2(x), ..., g_n(x), contínuas em [a,b][a,b] e obter nn constantes α1,α2,...,αn\alpha_1, \alpha_2, ..., \alpha_n tais que a função dada por:

f^(x)=α1g1(x)+α2g2(x)+...+αngn(x)\hat{f}(x) = \alpha_1g_1(x) +\alpha_2g_2(x) + ... + \alpha_n g_n(x)
seja a mais próxima possível de ff. Dizemos que este é um modelo matemático linear, pois os coeficientes α1,...,αn\alpha_1, ..., \alpha_n aparecem linearmente. As funções g1(x),...,gn(x)g_1(x), ..., g_n(x) podem ser funções não lineares de xx e a escolha destas funções é feita observando o gráfico dos pontos tabelados ou com base na teoria do experimento que forneceu os pontos.

Em geral ocorre que m>nm>n e, ao considerarmos que os pontos (x1,f(x1)),...,,(xm,f(xm))(x_1, f(x_1)), ...,, (x_m, f(x_m)) satisfazem a equação f^(x)=f(x)\hat{f}(x) = f(x), obtemos um sistema linear inconsistente, para o qual queremos encontrar uma solução de quadrados mínimos.

Digamos, por exemplo, que queremos ajustar um polinômio p(x)=α0+α1x+α2x2+...+αnxnp(x) = \alpha_0 + \alpha_1x +\alpha_2x^2 + ... + \alpha_nx^n aos pontos:

(x1,y1),(x2,y2),...,(xm,ym)(x_1, y_1), (x_2, y_2), ..., (x_m,y_m)
determinados. Consideramos que estes pontos satisfazem p(xi)=yip(x_i) = y_i, para i=1,...,mi = 1,..., m, isto é:

α0+α1x1+α2x12+...+αnx1n=y1α0+α1x2+α2x22+...+αnx2n=y2⋮α0+α1xm+α2xm2+...+αnxmn=ym\begin{array}{c} \alpha_0 +\alpha_1x_1 + \alpha_2x_1^2 + ... + \alpha_nx_1^n =y_1 \\ \alpha_0 + \alpha_1x_2 + \alpha_2x_2^2 + ...+ \alpha_nx_2^n = y_2 \\ \vdots \\ \alpha_0 +\alpha_1x_m + \alpha_2x_m^2 + ... + \alpha_nx_m^n =y_m \\ \end{array}
Este sistema de equações pode ser escrito na forma matricial como:

[1x1x12⋯x1n1x2x22⋯x2n⋮⋮⋮⋮1xmxm2⋯xmn][α0α1⋮αn]=[y1y2⋮ym]\left[ \begin{array}{ccccc} 1 &x_1 & x_1^2 & \cdots & x_1^n \\ 1 &x_2 & x_2^2 & \cdots & x_2^n \\ \vdots& \vdots & \vdots & & \vdots \\ 1& x_m & x_m^2 & \cdots & x_m^n\end{array} \right]\; \left[ \begin{array}{c}\alpha_0 \\ \alpha_1 \\ \vdots \\ \alpha_n\end{array} \right] = \left[ \begin{array}{c} y_1 \\y_2 \\ \vdots \\ y_m \end{array} \right]
Em geral, o grau do polinômio é bem menor que a quantidade de dados, ou seja, m>nm > n, e este sistema é inconsistente. Neste caso, os coeficientes α0,α1,...,αn\alpha_0, \alpha_1, ..., \alpha_n do polinômio cujo gráfico melhor se ajusta aos dados podem ser obtidos como uma solução de quadrados mínimos lineares.

Caso Não Linear

Em alguns casos, a expressão analítica para a curva de ajuste não é linear nos parâmetros αi\alpha_i, e temos que aplicar o método dos quadrados mínimos não lineares.

Por exemplo, se a curva de ajuste for φ(x)=α1eα2x\varphi(x) = \alpha_1e^{\alpha_2x} significa que de alguma forma os pontos tabelados se aproximam do gráfico desta curva, isto é:
y≈α1eα2xy \approx \alpha_1e^{\alpha_2x}
Para modelar este problema de forma linear, rearranjamos a expressão aplicando propriedades do logaritmo da seguinte forma:

y≈α1eα2x⇔ln(y)≈ln(α1eα2x)⇔ln(y)≈ln(α1)+α2xy \approx \alpha_1e^{\alpha_2x}\Leftrightarrow ln(y) \approxln(\alpha_1e^{\alpha_2x}) \Leftrightarrow ln(y)\approx ln(\alpha_1) + \alpha_2x
Chamando z=ln(y)z = ln(y), β1=ln(α1)\beta_1 = ln(\alpha_1) e β2=α2\beta_2 = \alpha_2, concluímos que se yy se aproxima de φ\varphi, então z=ln(y)z = ln(y) se aproxima de uma função linear em xx: z≈ϕ(x)=β1+β2xz \approx \phi(x) = \beta_1 +\beta_2x. Utilizamos o método de quadrados mínimos lineares para determinar os coeficientes β1\beta_1 e β2\beta_2, e posteriormente obtemos α1\alpha_1 e α2\alpha_2.

Voltar ao Topo.

Exemplos

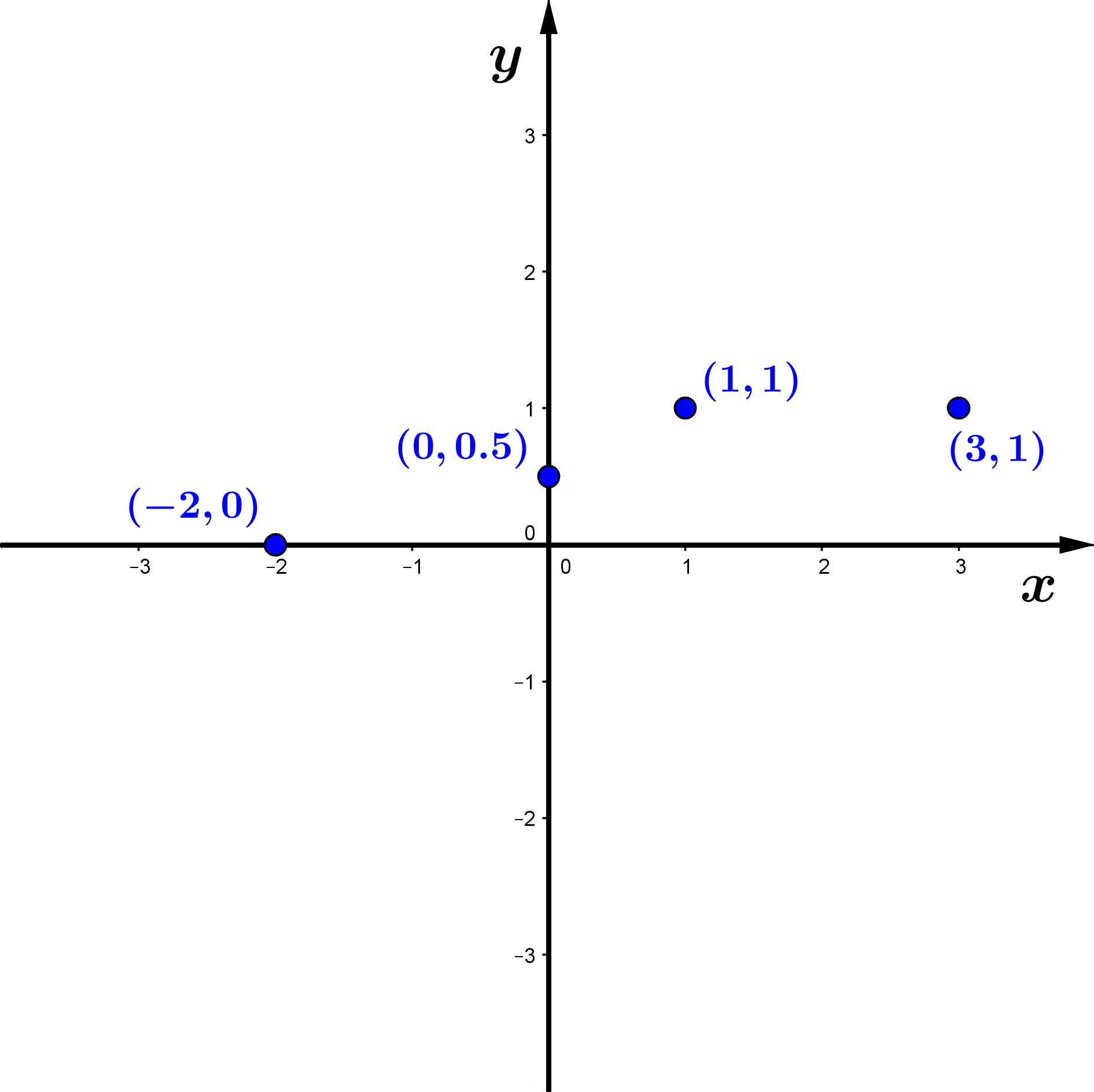
Exemplo 1: suponha que obtivemos os seguintes pontos experimentalmente: (-2,0),(0,0.5),(1,1)(-2,0), (0,0.5), (1,1) e (3,1)(3,1). Analisando os pontos no plano cartesiano, notamos que uma função linear é uma boa opção de ajuste aos pontos obtidos:
ajuste1
Figura 1: uma função linear é uma opção de ajuste aos pontos (-2,0),(0,0.5),(1,1)(-2,0), (0,0.5), (1,1) e (3,1)(3,1).

Queremos encontrar um polinômio da forma p(x)=a0+a1xp(x) = a_0 + a_1x. Supondo que todos os pontos satisfazem a equação polinomial, então:

{a0+a1(-2)=0a0+a10=0.5a0+a11=1a0+a13=1\left\lbrace \begin{array}{rrcrc} a_0& + & a_1(-2) & = & 0 \\ a_0 & +& a_10 & = & 0.5 \\ a_0 & + &a_11 & = & 1 \\ a_0 & + & a_13 &= & 1 \end{array} \right.
Escrevemos este sistema na forma matricial:

Av=b⇔[1-2101113][a0a1]=[00.511]Av = b \Leftrightarrow\left[\begin{array}{cr} 1 & -2 \\ 1 & 0 \\ 1& 1 \\ 1 & 3 \end{array}\right]\;\left[\begin{array}{c} a_0 \\ a_1\end{array}\right] = \left[\begin{array}{c} 0 \\ 0.5\\ 1 \\ 1 \end{array}\right]
Vamos determinar uma solução de quadrados mínimos deste sistema, utilizando a fatoração ortogonal da matriz AA. Com uma precisão de 4 casas decimais, obtemos:

A=QR=[-0.50000.6934-0.09600.5099-0.50000.1387-0.4018-0.7545-0.5000-0.13870.8428-0.1430-0.5000-0.6934-0.34500.3876][-2.0000-1.00000-3.60560000]A = QR = \left[\begin{array}{rrrr}-0.5000 & 0.6934 & -0.0960 & 0.5099 \\-0.5000 & 0.1387 & -0.4018 & -0.7545 \\-0.5000 & -0.1387 & 0.8428 & -0.1430 \\-0.5000 & -0.6934 & -0.3450 & 0.3876\end{array}\right] \; \left[\begin{array}{rr}-2.0000 & -1.0000 \\ 0 & -3.6056 \\ 0 &0 \\ 0 & 0 \end{array}\right]
onde QQ é uma matriz ortogonal. Da matriz RR extraímos a matriz 2×22\times 2 triangular superior:

R^=[−2.0000−1.00000−3.6056]\hat{R} = \left[\begin{array}{rr}-2.0000 & -1.0000 \\ 0 & -3.6056\end{array}\right]
Temos que QtAv=Qtb⇔Rv=cQ^tAv = Q^tb \Leftrightarrow Rv = c, onde:

c=Qtb=[-0.5000-0.5000-0.5000-0.50000.69340.1387-0.1387-0.6934-0.0960-0.40180.8428-0.34500.5099-0.7545-0.14300.3876][00.511]=[-1.2500-0.76270.2969-0.1326]c = Q^tb = \left[\begin{array}{rrrr}-0.5000 & -0.5000 & -0.5000 & -0.5000 \\0.6934 & 0.1387 & -0.1387 & -0.6934 \\-0.0960 & -0.4018 & 0.8428 & -0.3450 \\0.5099 & -0.7545 & -0.1430 & 0.3876\end{array}\right] \; \left[\begin{array}{c} 0 \\0.5 \\ 1 \\ 1 \end{array}\right] =\left[\begin{array}{r} -1.2500 \\ -0.7627 \\ 0.2969\\ -0.1326 \end{array}\right]
Do vetor cc extraímos o vetor:

c^=[-1.2500-0.7627]\hat{c} = \left[\begin{array}{r}-1.2500 \\ -0.7627 \end{array}\right]
Assim, temos o seguinte sistema triangular superior:

R^v=c^⇔[−2.0000−1.00000−3.6056][a0a1]=[−1.2500−0.7627]\hat{R}v = \hat{c} \Leftrightarrow\left[\begin{array}{rr} -2.0000 & -1.0000 \\ 0& -3.6056 \end{array}\right] \;\left[\begin{array}{rr} a_0 \\ a_1\end{array}\right] = \left[\begin{array}{r} -1.2500\\ -0.7627 \end{array}\right]
cuja solução (0.5192,0.2115)\left(0.5192, 0.2115 \right) é também uma solução de quadrados mínimos do sistema inicial. Portanto, o polinômio de grau 1:

p(x)=0.5192+0.2115xp(x) = 0.5192 + 0.2115x
é aquele que melhor se ajusta aos pontos obtidos, entre todos os possíveis polinômios de grau 1.

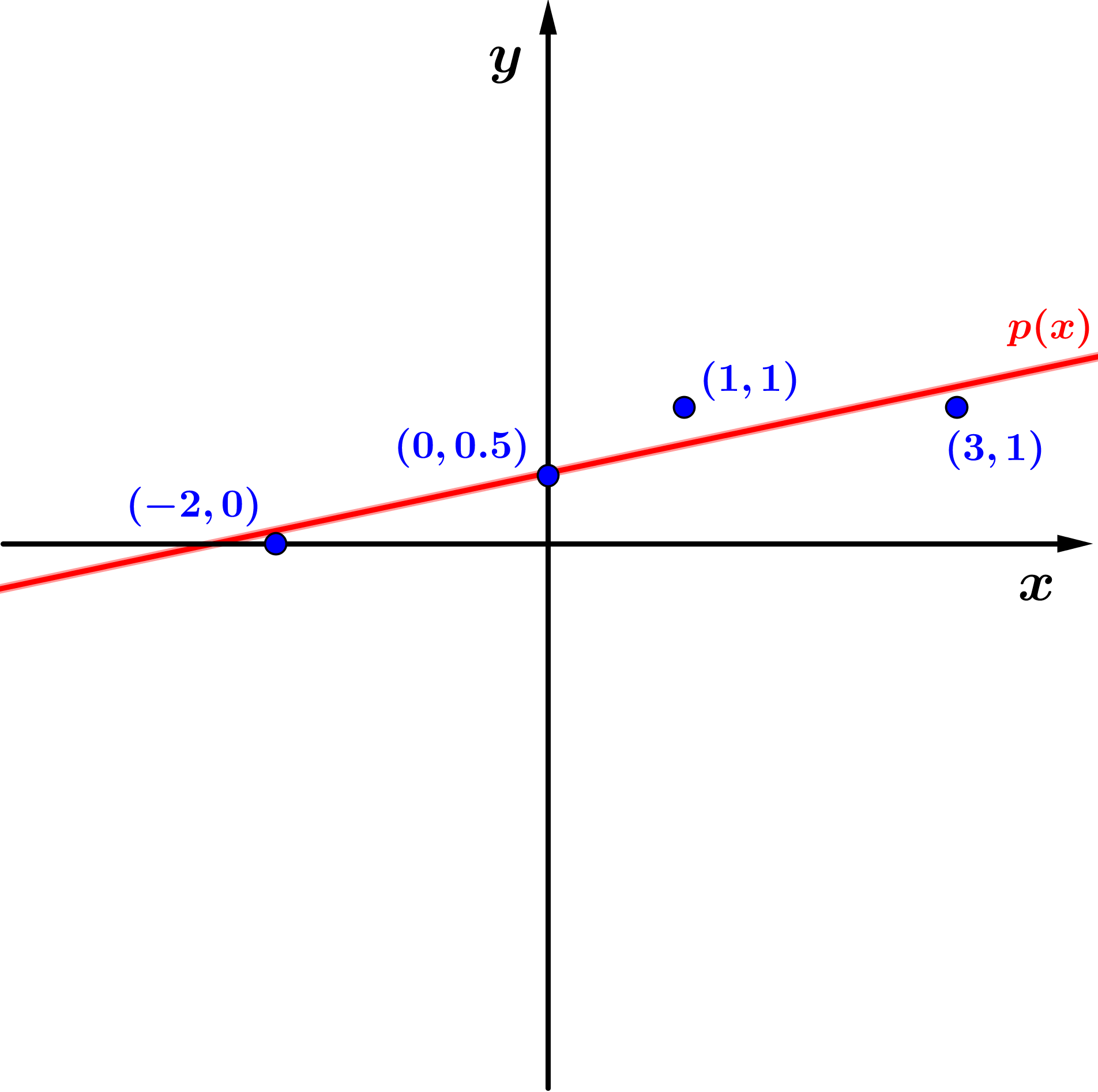
ajuste2
    Figura 2: o polinômio p(x)=0.5192+0.2115xp(x) = 0.5192 + 0.2115x é o que melhor se ajusta aos pontos.


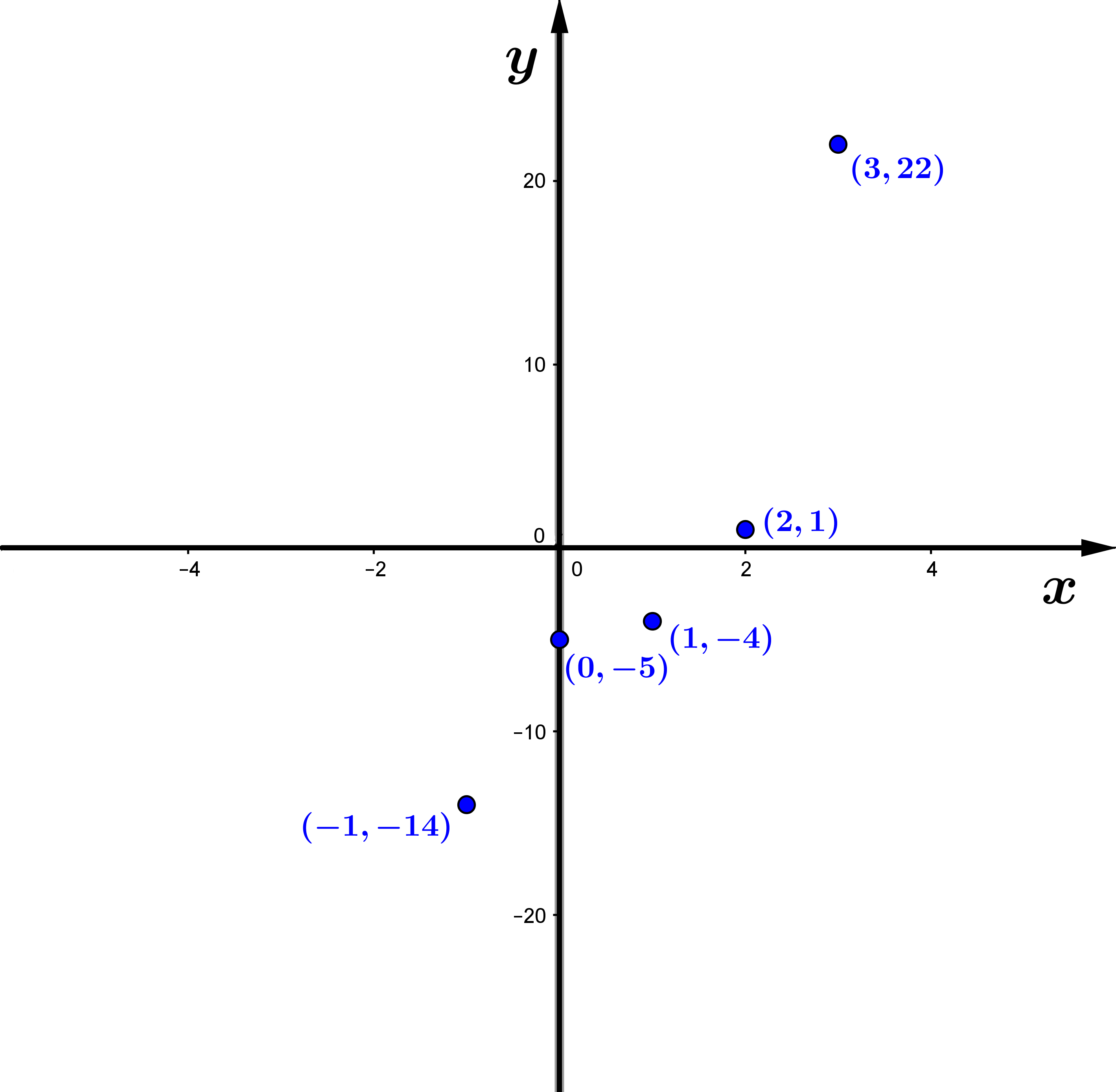
Exemplo 2: suponha que obtivemos experimentalmente a seguinte tabela de dados:
x
 -1
 0
 1
 2
 3
y
 -14
 -5
 -4
 1
 22

Analisando estes pontos no plano cartesiano, podemos supor que os valores de xx e yy estão relacionados por um polinômio de grau 3:
ajuste3
Figura 3: um polinômio de grau 3 é uma opção de ajuste aos pontos tabelados.

Queremos encontrar o polinômio cúbico p(x)=a0+a1x+a2x2+a3x3p(x) = a_0 + a_1x + a_2x^2 + a_3x^3 de melhor ajuste dos pontos (-1,-14),(0,-5),(1,-4),(2,1)(-1, -14), (0,-5), (1, -4), (2, 1) e (3,22)(3,22). Se os pontos satisfizessem a equação polinomial, então:

{a0+a1(-1)+a2(-1)2+a3(-1)3=-14a0+a10+a202+a303=-5a0+a11+a212+a313=-4a0+a12+a222+a323=1a0+a13+a232+a333=22⇔\left\lbrace \begin{array}{ccccccccr}a_0 & + & a_1(-1) & + & a_2(-1)^2& + & a_3(-1)^3 & = & -14 \\ a_0& + & a_1 0 & + & a_2 0^2 & +& a_3 0^3 & = & -5 \\ a_0 & + &a_1 1 & + & a_2 1^2 & + & a_3 1^3& = & -4 \\ a_0 & + & a_1 2 & +& a_2 2^2 & + & a_3 2^3 & = & 1\\ a_0 & + & a_1 3 & + & a_2 3^2& + & a_3 3^3 & = & 22 \end{array}\right. \;\;\;\;\;\;\; \Leftrightarrow
⇔{a0+a1(-1)+a21+a3(-1)=-14a0+a10+a20+a30=-5a0+a11+a21+a31=-4a0+a12+a24+a38=1a0+a13+a29+a327=22\Leftrightarrow\left\lbrace\begin{array}{ccccccccr} a_0 & + & a_1(-1)& + & a_21 & + & a_3(-1) & =& -14 \\ a_0 & + & a_1 0 & + &a_2 0 & + & a_3 0 & = & -5 \\ a_0& + & a_1 1 & + & a_2 1 & +& a_3 1 & = & -4 \\ a_0 & + &a_1 2 & + & a_2 4 & + & a_3 8 &= & 1 \\ a_0 & + & a_1 3 & + &a_2 9 & + & a_3 27 & = & 22\end{array} \right.
Escrevemos este sistema na forma matricial:

Av=b⇔[1-11-110001111124813927][a0a1a2a3]=[-14-5-4122]Av = b \Leftrightarrow\left[\begin{array}{rrrr} 1 & -1 & 1 &-1 \\ 1 & 0 & 0 & 0 \\ 1 & 1 & 1& 1 \\ 1 & 2 & 4 & 8 \\ 1 & 3& 9 & 27 \end{array}\right]\;\left[\begin{array}{c} a_0 \\ a_1 \\ a_2 \\ a_3\end{array}\right] = \left[\begin{array}{r} -14 \\-5 \\ -4 \\ 1 \\ 22 \end{array}\right]
Vamos determinar uma solução de quadrados mínimos utilizando a fatoração ortogonal da matriz AA. Utilizando uma precisão de 4 casas decimais, obtemos:

A=QR=A = QR =
=[-0.4472-0.63250.5345-0.3162-0.1195-0.4472-0.3162-0.26730.63250.4781-0.44720-0.53450-0.7171-0.44720.3162-0.2673-0.63250.4781-0.44720.63250.53450.3162-0.1195][-2.2361-2.2361-6.7082-15.652503.16236.324620.2386003.741711.22500003.79470000]= \left[\begin{array}{rrrrr} -0.4472& -0.6325 & 0.5345 & -0.3162 &-0.1195 \\ -0.4472 & -0.3162 & -0.2673 &0.6325 & 0.4781 \\ -0.4472 & 0 & -0.5345& 0 & -0.7171 \\ -0.4472 & 0.3162 &-0.2673 & -0.6325 & 0.4781 \\ -0.4472 &0.6325 & 0.5345 & 0.3162 & -0.1195\end{array}\right] \; \left[\begin{array}{rrrr}-2.2361 & -2.2361 & -6.7082 & -15.6525\\ 0 & 3.1623 & 6.3246 & 20.2386 \\ 0& 0 & 3.7417 & 11.2250 \\ 0 & 0& 0 & 3.7947 \\ 0 & 0 & 0 & 0\end{array}\right]
onde QQ é uma matriz ortogonal. Da matriz RR extraímos a matriz 4×44\times 4 triangular superior:

R^=[-2.2361-2.2361-6.7082-15.652503.16236.324620.2386003.741711.22500003.7947]\hat{R} = \left[\begin{array}{rrrr}-2.2361 & -2.2361 & -6.7082 & -15.6525\\ 0 & 3.1623 & 6.3246 & 20.2386 \\ 0& 0 & 3.7417 & 11.2250 \\ 0 & 0& 0 & 3.7947 \end{array}\right]
Temos que QtAv=Qtb⇔Rv=cQ^tAv = Q^tb \Leftrightarrow Rv = c, onde:

c=Qtb=[-0.4472-0.4472-0.4472-0.4472-0.4472-0.6325-0.316200.31620.63250.5345-0.2673-0.5345-0.26730.5345-0.31620.63250-0.63250.3162-0.11950.4781-0.71710.4781-0.1195][-14-5-4122]=[024.66587.48337.58950]c = Q^tb = \left[\begin{array}{rrrrr}-0.4472 & -0.4472 & -0.4472 & -0.4472& -0.4472 \\ -0.6325 & -0.3162 & 0 &0.3162 & 0.6325 \\ 0.5345 & -0.2673 &-0.5345 & -0.2673 & 0.5345 \\ -0.3162 &0.6325 & 0 & -0.6325 & 0.3162 \\ -0.1195& 0.4781 & -0.7171 & 0.4781 &-0.1195 \end{array}\right]\; \left[\begin{array}{r}-14 \\ -5 \\ -4 \\ 1 \\ 22 \end{array}\right] =\left[\begin{array}{c} 0 \\ 24.6658 \\ 7.4833 \\7.5895 \\ 0 \end{array}\right]
Do vetor cc extraímos o vetor:

c^=[024.66587.48337.5895]\hat{c} = \left[\begin{array}{c} 0 \\24.6658 \\ 7.4833 \\ 7.5895 \end{array}\right]
Assim, temos o sistema triangular superior:

R^v=c^⇔[-2.2361-2.2361-6.7082-15.652503.16236.324620.2386003.741711.22500003.7947][a0a1a2a3]=[024.66587.48337.5895]\hat{R}v = \hat{c} \Leftrightarrow\left[\begin{array}{rrrr} -2.2361 & -2.2361& -6.7082 & -15.6525 \\ 0 & 3.1623 &6.3246 & 20.2386 \\ 0 & 0 & 3.7417 &11.2250 \\ 0 & 0 & 0 & 3.7947\end{array}\right] \;\left[\begin{array}{rr} a_0 \\a_1 \\ a_2 \\ a_3 \end{array}\right] =\left[\begin{array}{c} 0 \\ 24.6658 \\ 7.4833 \\7.5895 \end{array}\right]
cuja solução (-5,3,-4,2)\left(-5, 3, -4, 2 \right) é também uma solução de quadrados mínimos do sistema inicial. Portanto, o polinômio de grau 3:

p(x)=-5+3x-4x2+2x3p(x) = -5 + 3x - 4x^2 + 2x^3
é o que melhor se ajusta aos pontos tabelados, entre todos os polinômios de grau 3.
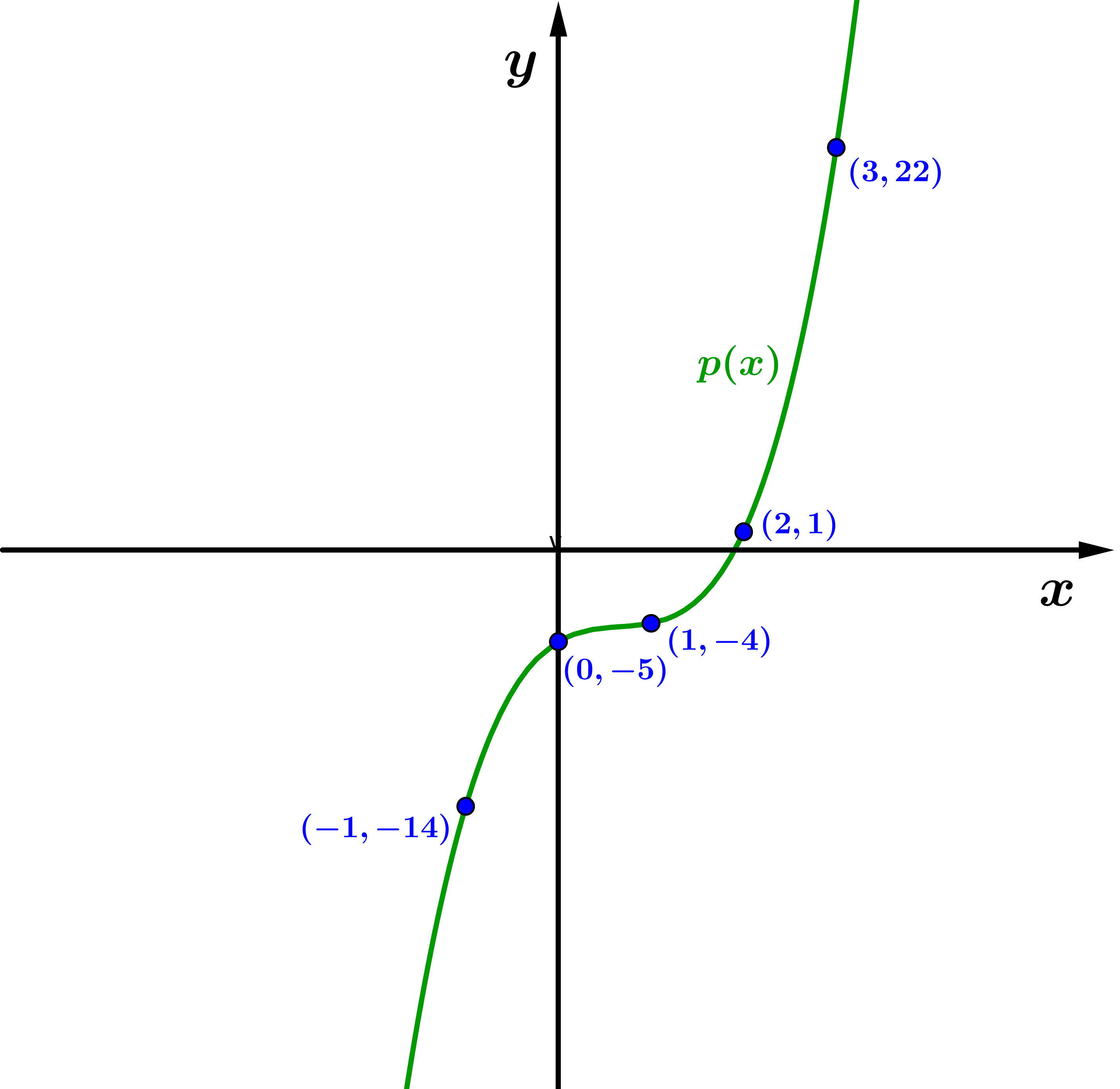
ajuste4
 
Figura 4: o polinômio p(x)=-5+3x-4x2+2x3p(x) = -5 + 3x - 4x^2 + 2x^3 é o que melhor se ajusta aos pontos.
Última Atualização: 04/08/2016.