Problemas Aplicados - Ajuste de Curvas

, para facilitar os cálculos e reduzir os erros de arredondamentos.

Uma curva logística é empregada para descrever um processo de crescimento populacional. Uma expressão analítica para esta curva é:

P(t) = \frac{L}{1 + \alpha_1 e^{\alpha_2 t}}

onde

L

é a saturação do processo, que representa o limite desta população quando

t \rightarrow \infty

. Neste exemplo, vamos considerar

L = 500

e encontrar uma curva logística para a população do Brasil através do método de quadrados mínimos, utilizando os dados tabelados.

Note que esta curva de ajuste não é linear nos parâmetros

\alpha_1

\alpha_2

e, neste caso, precisamos realizar algumas transformações em sua expressão, que resultem em uma curva linear nos parâmetros a serem determinados. No caso, temos:

pop(t) \approx P(t) = \frac{L}{1 + \alpha_1e^{\alpha_2t}} \Leftrightarrow \frac{1}{pop(t)} \approx \frac{1 + \alpha_1e^{\alpha_2t}}{L} \Leftrightarrow \frac{L}{pop(t)} - 1 \approx \alpha_1e^{\alpha_2t}

Definimos:

z(t) = \frac{L}{pop(t)} - 1

e teremos então:

z(t) \approx \alpha_1e^{\alpha_2t} \Leftrightarrow ln(z(t)) \approx ln(\alpha_1) + \alpha_2t

Vamos ajustar

ln(z(t))

por

ln(\alpha_1) + \alpha_2t

. Utilizando a notação

\beta_1 = ln(\alpha_1)

\beta_2 = \alpha_2

, a curva

\varphi(t) = \beta_1 + \beta_2t

é linear nos parâmetros

\beta_1

\beta_2

. Estes parâmetros podem ser obtidos pelo método dos quadrados mínimos lineares e, fazendo as substituições adequadas, obtém-se os valores para

\alpha_1

\alpha_2

.

Utilizando os dados tabelados para

pop(t)

, calculamos os valores para

z(t)

ln(z(t))

$t$	1	3	4	5	6	7	8.1	9	10
$pop(t)$	30.6	41.2	51.9	70.2	93.1	119.0	146.2	169.8	190.7
$z(t)$	15.3399	11.1359	8.6339	6.1225	4.3706	3.2017	2.4200	1.9446	1.6219
$ln(z(t))$	2.7305	2.4102	2.1557	1.8120	1.4749	1.1637	0.8838	0.6651	0.4836

Supondo que estes dados satisfazem a expressão

\varphi(t) = \beta_1 + \beta_2t

, obtemos o seguinte sistema linear na forma matricial

Ax = b

\left[\begin{array}{cc} 1 & 1 \\ 1 & 3 \\ 1 & 4 \\ 1 & 5 \\ 1 & 6 \\ 1 & 7 \\ 1 & 8.1 \\ 1 & 9 \\ 1 & 10 \end{array}\right] \;\left[\begin{array}{r} \beta_1 \\ \beta_2 \end{array}\right] = \left[\begin{array}{r} 2.7305 \\ 2.4102 \\ 2.1557 \\ 1.8120 \\ 1.4749 \\ 1.1637 \\ 0.8838 \\ 0.6651 \\ 0.4836 \end{array}\right]

Pela fatoração ortogonal da matriz dos coeficientes, obtemos a matriz ortogonal

Q \in \mathbb{R}^9 \times \mathbb{R}^9

e a matriz triangular superior:

R = \left[\begin{array}{rr} -3.0000 & -17.7000 \\ 0 & 8.3259 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{array}\right]

tais que

A = QR

. Logo,

Ax = b \Leftrightarrow QRx = b \Leftrightarrow Rx = Q^tb

, onde usamos a propriedade da matriz ortogonal:

Q^t = Q^{-1}

. Chamando

c = Q^tb

, temos:

Rx = c \Leftrightarrow \left[\begin{array}{rr} -3.0000 & -17.7000 \\ 0 & 8.3259 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{array}\right] \; \left[\begin{array}{r} \beta_1 \\ \beta_2 \end{array}\right] = \left[\begin{array}{r} -4.5932 \\ -2.2435 \\ 0.1343 \\ 0.0728 \\ 0.0180 \\ -0.0110 \\ 0.0196 \\ 0.0549 \\ 0.1557 \end{array}\right]

Como abaixo da linha 2 a matriz

R

é nula, esta parte do sistema não depende do vetor

x

. Assim, da matriz

R

e do vetor

c

extraímos a matriz

\hat{R}

e o vetor

\hat{c}

, respectivamente, dados por:

\hat{R} = \left[\begin{array}{rr} -3.0000 & -17.7000 \\ 0 & 8.3259 \end{array}\right] \;\;\;\; e \;\;\;\; \hat{c} = \left[ \begin{array}{r} -4.5932 \\ -2.2435 \end{array} \right]

e resolvemos o sistema linear

\hat{R}x = \hat{c}

\left[\begin{array}{rr} -3.0000 & -17.7000 \\ 0 & 8.3259 \end{array}\right] \;\left[\begin{array}{r} \beta_1 \\ \beta_2 \end{array}\right] = \left[ \begin{array}{r} -4.5932 \\ -2.2435 \end{array} \right]

obtendo a solução

\beta_1 = 3.1209

\beta_2 = -0.2695

. Agora, podemos determinar os parâmetros

\alpha_1

\alpha_2

\left\lbrace \begin{array}{l} \beta_1 = ln(\alpha_1) \\ \beta_2 = \alpha_2 \end{array}\right. \Leftrightarrow \left\lbrace \begin{array}{l} \alpha_1 = e^{\beta_1} = 22.6668\\ \alpha_2 = -0.2695 \end{array}\right.

Portanto, uma aproximação da curva logística para a população do Brasil é:

pop(t) \approx P(t) = \frac{500}{1 + 22.6668e^{-0.2695t}}

Vamos calcular os resíduos ponto a ponto da curva de ajuste com relação aos dados tabelados para

pop(t)

. Para isto, obtemos o vetor de resíduos

r = pop(t) - P(t)

. Com esta notação queremos dizer que cada coordenada do vetor

r

é dada pelo valor de

pop(t)

menos o valor da função

P(t)

para cada valor tabelado do tempo

t

. Temos:

$pop(t)$	30.6	41.2	51.9	70.2	93.1	119.0	146.2	169.8	190.7
$P(t)$	27.3045	45.0505	57.3858	72.5599	90.9222	112.7060	140.6572	166.4163	197.5527
$r(t)$	3.2955	-3.8505	-5.4858	-2.3599	2.1778	6.2940	5.5428	3.3837	-6.8527

A soma dos quadrados dos resíduos é

\left\|r\right\|_2^2 = 194.8386

.

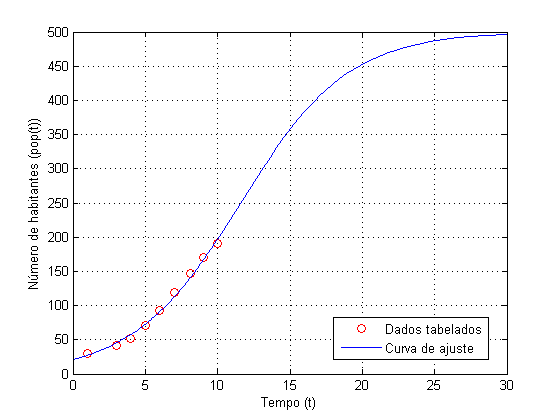
Construindo um gráfico com os dados tabelados para o número de habitantes no Brasil e a curva de ajuste, temos:

Podemos prever o número de habitantes no ano de 2017, por exemplo, calculando o valor da função

P(t)

para

t = 10.7

P(10.7) = \frac{500}{1 + 22.6668e^{-0.2695\times 10.6}} = 220.4819

o que indica que a população atingirá aproximadamente 220481900 habitantes.

Voltar ao Topo.

Problema 2 (Número de Acidentes com Veículos)

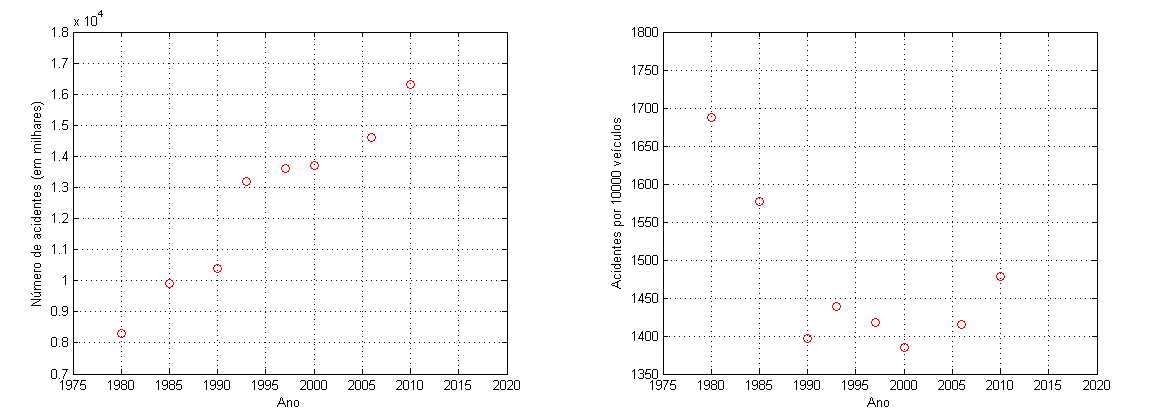
A tabela a seguir mostra o número total de acidentes com veículos motorizados e o número de acidentes por 10000 veículos no Brasil em alguns anos entre 1980 e 2010.

Ano	Número de Acidentes (em milhares)	Acidentes por 10000 veículos
1980	8300	1688
1985	9900	1577
1990	10400	1397
1993	13200	1439
1997	13600	1418
2000	13700	1385
2006	14600	1415
2010	16300	1478

Estes valores não são reais e estamos utilizando-os apenas como exemplo. Representamos os dados através do tempo (em anos) em dois gráficos, da seguinte forma:

Vamos calcular uma regressão linear (ajustando por um polinômio de grau 1) do número de acidentes no tempo, e uma regressão quadrática (ajustando por um polinômio de grau 2) do número de acidentes por 10000 veículos no tempo. Podemos utilizar estas curvas de ajuste para prever os dados no ano 2017, por exemplo. Isto é chamado análise de série temporal, visto que são regressões no tempo, e é utilizado para se ter uma previsão dos dados no futuro.

Em problemas como este, envolvendo datas contemporâneas, é interessante transladar os dados iniciais antes dos cálculos, pois isto reduzirá os erros de arredondamento. Assim, no lugar dos valores 1980, 1985, ..., 2010 utilizaremos 0, 5, ..., 30. Para facilitar, também podemos utilizar 8.3, 9.9, ..., 16.3 no lugar de 8300000, 9900000, ..., 16300000.

Primeiramente, vamos obter um ajuste linear do número de acidentes no tempo, ou seja, queremos ajustar os dados tabelados por um polinômio da forma:

p(t) = \alpha_1 + \alpha_2t

onde

t

representa o tempo (em anos) e

p(t)

o número de acidentes naquele ano. Supondo que os valores tabelados satisfazem esta relação, obtemos o sistema linear na forma matricial

Ax = b

\left[\begin{array}{rr} 1 & 0 \\ 1 & 5 \\ 1 & 10 \\ 1 & 13 \\ 1 & 17 \\ 1 & 20 \\ 1 & 26 \\ 1 & 30 \end{array}\right] \;\left[\begin{array}{r} \alpha_1 \\ \alpha_2 \end{array}\right] = \left[\begin{array}{r} 8.3 \\ 9.9 \\ 10.4 \\ 13.2 \\ 13.6 \\ 13.7 \\ 14.6 \\ 16.3 \end{array}\right]

Este sistema é claramente inconsistente. Utilizaremos o método de quadrados mínimos para obter uma solução

x = (\alpha_1, \alpha_2)

que minimiza

\left\|Ax-b\right\|_2^2

. Pela fatoração ortogonal da matriz

A

, obtemos a matriz

Q \in \mathbb{R}^8 \times \mathbb{R}^8

ortogonal e a matriz triangular superior:

R = \left[\begin{array}{rr} -2.8284 & -42.7800 \\ 0 & 26.9977 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{array}\right]

tais que

A = QR

. Temos então:

Ax = b \Leftrightarrow QRx = b \Leftrightarrow Rx = Q^tb

, uma vez que a matriz

Q

é ortogonal. Chamando

c = Q^tb

, temos:

Rx = c \Leftrightarrow \left[\begin{array}{rr} -2.8284 & -42.7800 \\ 0 & 26.9977 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{array}\right] \;\left[\begin{array}{r} \alpha_1 \\ \alpha_2 \end{array}\right] = \left[\begin{array}{r} -35.3553 \\ 6.9043 \\ -0.7053 \\ 1.3343 \\ 0.7206 \\ 0.0602 \\ -0.5604 \\ 0.1258 \end{array}\right]

Da matriz

R

e do vetor

c

podemos extrair a matriz

\hat{R}

e o vetor

\hat{c}

, respectivamente, dados por:

\hat{R} = \left[\begin{array}{rr} -2.8284 & -42.7800 \\ 0 & 26.9977 \end{array}\right] \;\;\;\; e \;\;\;\; \hat{c} = \left[ \begin{array}{r} -35.3553 \\ 6.9043 \end{array} \right]

e resolvemos então o sistema linear:

\hat{R}x = \hat{c} \Leftrightarrow \left[\begin{array}{rr} -2.8284 & -42.7800 \\ 0 & 26.9977 \end{array}\right] \;\left[ \begin{array}{r} \alpha_1 \\ \alpha_2 \end{array} \right] = \left[ \begin{array}{r} -35.3553 \\ 6.9043 \end{array} \right]

obtendo a solução

\alpha_1 = 8.6320

\alpha_2 = 0.2557

. Como esta é uma solução exata de

\hat{R}x = \hat{c}

, temos que

\left\|\hat{R}x - \hat{c} \right\|_2^2 = 0

e, portanto, a soma dos quadrados dos resíduos de

r = Ax-b

, que é igual a dos resíduos de

s = Rx-c

, é dada pela parte do vetor

c

que sobrou ao extrairmos o vetor

\hat{c}

, assim:

\left\|r\right\|_2^2 = \left\|(-0.7053, 1.3343, 0.7206, 0.0602, -0.5604, 0.1258)\right\|_2^2 = 3.1306

Este valor é mínimo, visto que a solução obtida é solução de quadrados mínimos do sistema

Ax = b

. Portanto, obtivemos os coeficientes de um polinômio de grau 1 que melhor se ajusta aos dados tabelados:

p(t) = 8.6320 + 0.2557t

cujo gráfico representamos a seguir:

Podemos utilizar este polinômio para calcular

p(37)

, por exemplo:

p(37) = 8.6320 + 0.2557(37) = 18.0929

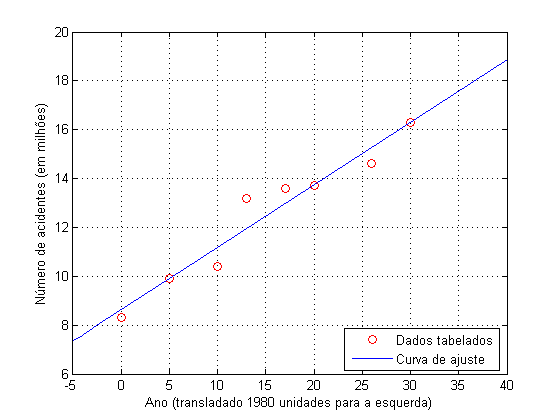
obtendo assim uma estimativa de 18092900 acidentes com veículos motorizados no ano 2017.

Vamos agora ajustar o número de acidentes por 10000 veículos no tempo por um polinômio de grau 2, da forma:

p(t) = \beta_1 + \beta_2x +\beta_3x^2

onde

t

representa o tempo (em anos) e

p(t)

o número de acidentes por 10000 veículos naquele ano. Para facilitar os cálculos, no lugar de 1688, 1577, ..., 1478 utilizaremos 1.688, 1.577, ..., 1.478. Supomos que os valores tabelados satisfazem este polinômio, obtendo o sistema linear na forma matricial

Ax=b

\left[\begin{array}{rrr} 1 & 0 & 0^2 \\ 1 & 5 & 5^2 \\ 1 & 10 & 10^2 \\ 1 & 13 & 13^2 \\ 1 & 17 & 17^2 \\ 1 & 20 & 20^2 \\ 1 & 26 & 26^2 \\ 1 & 30 & 30^2 \end{array} \right]\;\left[\begin{array}{r} \beta_1 \\ \beta_2 \\ \beta_3 \end{array} \right] = \left[\begin{array}{r} 1.688 \\ 1.577 \\ 1.397 \\ 1.439 \\ 1.418 \\ 1.385 \\ 1.415 \\ 1.478 \end{array} \right] \Leftrightarrow \left[\begin{array}{rrr} 1 & 0 & 0 \\ 1 & 5 & 25 \\ 1 & 10 & 100 \\ 1 & 13 & 169 \\ 1 & 17 & 289 \\ 1 & 20 & 400 \\ 1 & 26 & 676 \\ 1 & 30 & 900 \end{array} \right]\;\left[\begin{array}{r} \beta_1 \\ \beta_2 \\ \beta_3 \end{array} \right] = \left[\begin{array}{r} 1.688 \\ 1.577 \\ 1.397 \\ 1.439 \\ 1.418 \\ 1.385 \\ 1.415 \\ 1.478 \end{array} \right]

Este sistema também é inconsistente e vamos utilizar o método de quadrados mínimos para obter uma solução que minimize

\left\|Ax-b\right\|_2

. Na fatoração ortogonal da matriz

A

, obtemos a matriz

Q \in \mathbb{R}^8 \times \mathbb{R}^8

ortogonal e a matriz triangular superior:

R = \left[\begin{array}{rrr} -2.8284 & -42.7800 & -904.7431 \\ 0 & 26.9977 & 818.8156 \\ 0 & 0 & 246.3005 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right]

tais que

A = QR

. Temos então:

Ax = b \Leftrightarrow QRx = b \Leftrightarrow Rx = Q^tb

, uma vez que a matriz

Q

é ortogonal. Considerando

c = Q^tb

, temos:

Rx = c \Leftrightarrow \left[\begin{array}{rrr} -2.8284 & -42.7800 & -904.7431 \\ 0 & 26.9977 & 818.8156 \\ 0 & 0 & 246.3005 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right] \;\left[\begin{array}{r} \beta_1 \\ \beta_2 \\ \beta_3 \end{array}\right] = \left[\begin{array}{r} -4.1709 \\ -0.1827 \\ 0.1984 \\ 0.0430 \\ 0.0538 \\ 0.0240 \\ 0.0075 \\ 0.0002 \end{array}\right]

Da matriz

R

e do vetor

c

extraímos a matriz

\hat{R}

e o vetor

\hat{c}

\hat{R} = \left[\begin{array}{rrr} -2.8284 & -42.7800 & -904.7431 \\ 0 & 26.9977 & 818.8156 \\ 0 & 0 & 246.3005 \end{array}\right] \;\;\;\; e \;\;\;\; \hat{c} = \left[\begin{array}{r} -4.1709 \\ -0.1827 \\ 0.1984 \end{array}\right]

Resolvemos então o sistema linear

\hat{R}x = \hat{c}

\left[\begin{array}{rrr} -2.8284 & -42.7800 & -904.7431 \\ 0 & 26.9977 & 818.8156 \\ 0 & 0 & 246.3005 \end{array}\right] \;\left[\begin{array}{r} \beta_1 \\ \beta_2 \\ \beta_3 \end{array}\right] = \left[\begin{array}{r} -4.1709 \\ -0.1827 \\ 0.1984 \end{array}\right]

obtendo a solução

\beta_1 = 1.6888

\beta_2 = -0.0312

\beta_3 = 0.0008

. A soma dos quadrados dos resíduos de

r = Ax-b

é dada apenas pela parte do vetor c que sobrou ao extrairmos o vetor

\hat{c}

, assim:

\left\|r\right\|_2^2 = \left\|(0.0430, 0.0538, 0.0240, 0.0075, 0.0002)\right\|_2^2 = 0.0056

Portanto, obtivemos os coeficientes de um polinômio de grau 2 que melhor se ajusta aos dados tabelados:

p(t) = 1.6888 - 0.0312t + 0.0008t^2

cujo gráfico representamos a seguir:

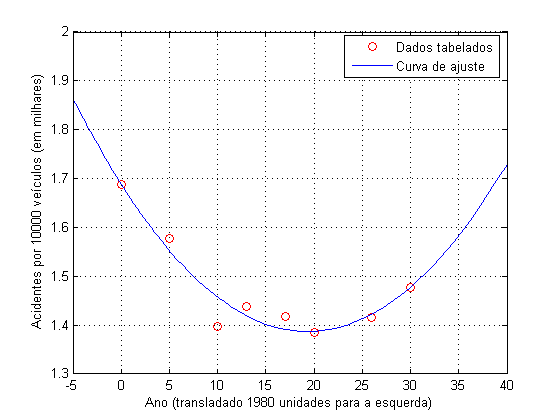
Podemos utilizar este polinômio para calcular

p(37)

, por exemplo:

p(37) = 1.6888 - 0.0312(37) + 0.0008(37)^2 = 1.6373

obtendo assim uma estimativa de 1637.3 acidentes por 10000 veículos no ano 2017.

Voltar ao Topo.

Problema 3 (Resistência à Compressão do Concreto)

A resistência à compressão do concreto,

\sigma

, decresce com o aumento da razão água/cimento,

\frac{w}{c}

(em galões de água por saco de cimento). Os valores da resistência à compressão de três amostras para várias razões de água por cimento estão mostrados na tabela a seguir:

$\frac{w}{c}$	4.5	5.0	5.5	6.0	6.5	7.0	7.5	8.0	8.5	9.0
$\sigma$	7000	6125	5237	4665	4123	3810	3107	3070	2580	2287

Podemos representar estes valores graficamente da seguinte forma:

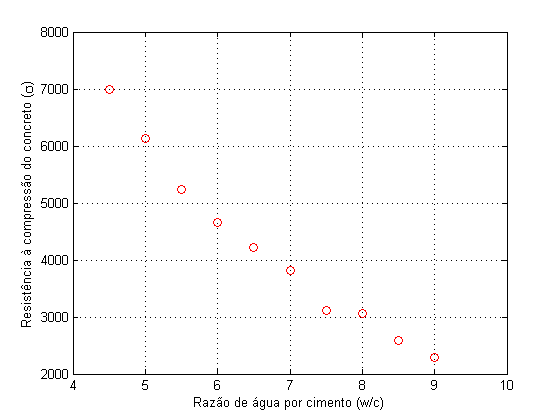
Estamos interessados em obter uma relação entre a resistência à compressão do concreto e a razão água/cimento. Observando o gráfico, podemos supor que estes valores se relacionam, aproximadamente, por uma função exponencial do tipo:

\sigma \approx f\left(\frac{w}{c}\right) = \alpha_1e^{-\alpha_2\frac{w}{c}}

.

Para modelar este problema de forma linear, rearranjamos a equação aplicando propriedades do logaritmo da seguinte forma:

\sigma \approx \alpha_1e^{-\alpha_2\frac{w}{c}} \Rightarrow \ln(\sigma) \approx \ln(\alpha_1e^{-\alpha_2\frac{w}{c}}) = \ln(\alpha_1) + \ln(e^{-\alpha_2\frac{w}{c}}) \Rightarrow

\Rightarrow \ln(\sigma) \approx \ln(\alpha_1) - \alpha_2\frac{w}{c}

Chamando

\beta_1 = \ln(\alpha_1)

\beta_2 = -\alpha_2

, temos que:

\ln(\sigma) \approx \beta_1 + \beta_2\frac{w}{c}

Utilizaremos o método de quadrados mínimos para determinar os coeficientes

\beta_1

\beta_2

, e posteriormente obter os coeficientes

\alpha_1

\alpha_2

. Neste caso, encontraremos os parâmetros

\beta_1

\beta_2

que minimizam a soma de quadrados dos resíduos entre

ln(\sigma)

e a função linear acima. Estamos resolvendo de forma aproximada o problema real que é: minimizar a soma de quadrados dos resíduos entre

\sigma

\alpha_1e^{-\alpha_2\frac{w}{c}}

e a função . Supondo que os pontos tabelados satisfazem a relação acima, obtemos o sistema linear na forma matricial

Ax = b

\left[ \begin{array}{cc} 1 & 4.5 \\ 1 & 5.0 \\ 1 & 5.5 \\ 1 & 6.0 \\ 1 & 6.5 \\ 1 & 7.0 \\ 1 & 7.5 \\ 1 & 8.0 \\ 1 & 8.5 \\ 1 & 9.0 \end{array} \right] \; \left[ \begin{array}{c} \beta_1 \\ \beta_2 \end{array} \right] = \left[ \begin{array}{c} \ln(7000) \\ \ln(6125) \\ \ln(5237) \\ \ln(4665) \\ \ln(4123) \\ \ln(3810) \\ \ln(3107) \\ \ln(3070) \\ \ln(2580) \\ \ln(2287) \end{array}\right] = \left[ \begin{array}{c} 8.8537 \\ 8.7201 \\ 8.5635 \\ 8.4478 \\ 8.3243 \\ 8.2454 \\ 8.0414 \\ 8.0294 \\ 7.8555 \\ 7.7350 \end{array} \right]

Esse sistema é claramente inconsistente e queremos obter uma solução de quadrados mínimos, que minimiza

\left\|Ax-b\right\|_2

. Obtendo a fatoração ortogonal

A = QR

da matriz dos coeficientes deste sistema, determinamos a matriz

Q \in \mathbb{R}^{10} \times \mathbb{R}^{10}

ortogonal e a matriz triangular superior:

R = \left[\begin{array}{rr} -3.1623 & -21.3454 \\ 0 & 4.5415 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{array} \right]

Como

A = QR

, temos que

Ax = b \Leftrightarrow QRx = b \Leftrightarrow Rx = Q^tb

, uma vez que

Q

é uma matriz ortogonal. Chamando

c = Q^tb

, temos:

Rx = c \Leftrightarrow \left[\begin{array}{rr} -3.1623 & -21.3454 \\ 0 & 4.5415 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{array} \right] \; \left[\begin{array}{r} \beta_1 \\ \beta_2 \end{array} \right] = \left[ \begin{array}{r} -26.1888 \\ -1.1059 \\ -0.0291 \\ -0.0225 \\ -0.0237 \\ 0.0197 \\ -0.0619 \\ 0.0484 \\ -0.0032 \\ -0.0014 \end{array} \right]

Da matriz

R

e do vetor

c

extraímos a matriz triangular superior

\hat{R}

e o vetor

\hat{c}

, respectivamente, dados por:

\hat{R} = \left[\begin{array}{rr} -3.1623 & -21.3454 \\ 0 & 4.5415 \end{array}\right] \;\;\;\; e \;\;\;\; \hat{c} = \left[ \begin{array}{r} -26.1888 \\ -1.1059 \end{array} \right]

Resolvemos então o sistema linear

\hat{R}x = \hat{c}

\left[\begin{array}{rr} -3.1623 & -21.3454 \\ 0 & 4.5415 \end{array}\right] \;\left[\begin{array}{r} \beta_1 \\ \beta_2 \end{array}\right] = \left[ \begin{array}{r} -26.1888 \\ -1.1059 \end{array} \right]

obtendo a solução

\beta_1 = 9.9253

\beta_2 = -0.2435

, que é a solução de quadrados mínimos do sistema

Ax = b

. Como esta é uma solução exata do sistema

\hat{R}x = \hat{c}

, temos que

\left\|\hat{R}x - \hat{c} \right\|_2^2 = 0

e, portanto, a soma dos quadrados dos resíduos de

r = Ax-b

, que é igual a dos resíduos de

s = Rx-c

, é dada pela parte do vetor

c

que sobrou ao extrairmos o vetor

\hat{c}

, ou seja:

\left\|r\right\|_2^2 = \left\| (-0.0291, -0.0225, -0.0237, 0.0197, -0.0619, 0.0484, -0.0032, -0.0014) \right\|_2^2 = 0.0085

Com os coeficientes

\beta_1

\beta_2

determinados, temos:

\left\lbrace \begin{array}{l} \beta_1 = \ln(\alpha_1) \\ \beta_2 = -\alpha_2 \end{array}\right. \Leftrightarrow \left\lbrace \begin{array}{l} \alpha_1 = e^{\beta_1} = e^{9.9253}\\ \alpha_2 = -\beta_2 = 0.2435 \end{array}\right.

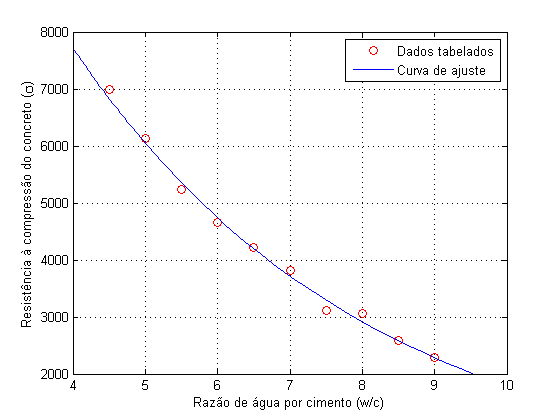
Portanto, os dados tabelados podem ser ajustados pela função dada por:

f\left(\frac{w}{c}\right) = \sigma = e^{9.9253}e^{-0.2435\frac{w}{c}} = e^{9.9253\; - \;0.2435\frac{w}{c}}

Assim, obtivemos uma curva de ajuste à tabela que nos fornece uma melhor estimativa da resistência à compressão do concreto dada uma razão água/cimento qualquer.

Vamos calcular o resíduo "real", isto é, da curva de ajuste com relação aos dados tabelados para

\sigma

. Para isto, obtemos o vetor de resíduos

v = \sigma - f\left( \frac{w}{c}\right)

, onde cada coordenada é dada pelo valor de

\sigma

menos o valor da função

f\left( \frac{w}{c}\right) = e^{9.9253\; - \;0.2435\frac{w}{c}}

para cada valor tabelado da razão w/c. Temos então:

\|v\|_2^2 \approx 12632

.

Voltar ao Topo.

Problema 4 (Quantidade Ideal de Calorias)

A tabela a seguir relaciona a quantidade ideal de calorias, em função da idade e do peso, para homens que possuem atividade física moderada e vivem a uma temperatura ambiente de 20ºC.

$(p,i)$	25	45	65
50	2500	2350	1950
60	2850	2700	2250
70	3200	3000	2550
80	3550	3350	2800

Usando o método de quadrados mínimos, vamos encontrar uma expressão da forma:

cal = \alpha p + \beta i

que aproxime os dados da tabela, onde

p

representa o peso (em kg),

i

a idade (em anos) e

cal

a quantidade ideal de calorias. Supondo que os dados tabelados satisfazem esta expressão, obtemos o seguinte sistema linear na forma matricial

Ax = b

\left[ \begin{array}{cc} 50 & 25 \\ 50 & 45 \\ 50 & 65 \\ 60 & 25 \\ 60 & 45 \\ 60 & 65 \\ 70 & 25 \\ 70 & 45 \\ 70 & 65 \\ 80 & 25 \\ 80 & 45 \\ 80 & 65 \end{array} \right] \;\left[ \begin{array}{c} \alpha \\ \beta \end{array} \right] = \left[ \begin{array}{c} 2500 \\ 2350 \\ 1950 \\ 2850 \\ 2700 \\ 2250 \\ 3200 \\ 3000 \\ 2550 \\ 3550 \\ 3350 \\ 2800 \end{array} \right]

Claramente, este sistema é inconsistente. Obtendo a fatoração ortogonal da matriz dos coeficientes, determinamos a matriz

Q \in \mathbb{R}^{12} \times \mathbb{R}^{12}

ortogonal e a matriz triangular superior:

R = \left[ \begin{array}{rr} -228.4732 & -153.6285 \\ 0 & -62.4362 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{array} \right]

tais que

A = QR

. Temos então que:

Ax = b \Leftrightarrow QRx = b \Leftrightarrow Rx = Q^tb

, uma vez que

Q

é ortogonal. Chamando

c = Q^tb

, temos:

Rx = c \Leftrightarrow \left[ \begin{array}{rr} -228.4732 & -153.6285 \\ 0 & -62.4362 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{array} \right] \;\left[ \begin{array}{c} \alpha \\ \beta \end{array} \right] = 10^3 \left[ \begin{array}{r} -9.6138 \\ 0.6520 \\ -0.0166 \\ 0.1546 \\ 0.1312 \\ -0.1922 \\ 0.0290 \\ -0.0444 \\ -0.3678 \\ -0.0966 \\ -0.1700 \\ -0.5935 \end{array} \right]

Como abaixo da linha 2 a matriz

R

é nula, esta parte do sistema não depende do vetor

x

. Assim, da matriz

R

e do vetor

c

extraímos a matriz

\hat{R}

e o vetor

\hat{c}

, respectivamente, dados por:

\hat{R} = \left[\begin{array}{rr} -228.4732 & -153.6285 \\ 0 & -62.4362 \end{array}\right] \;\;\;\; e \;\;\;\; \hat{c} = 10^3 \left[ \begin{array}{r} -9.6138 \\ 0.6520 \end{array} \right]

Resolvemos então o sistema linear

\hat{R}x = \hat{c}

\left[\begin{array}{rr} -228.4732 & -153.6285 \\ 0 & -62.4362 \end{array}\right] \;\left[ \begin{array}{r} \alpha \\ \beta \end{array} \right]= 10^3\; \left[ \begin{array}{r} -9.6138 \\ 0.6520 \end{array} \right]

obtendo a solução

\alpha = 49.1001

\beta = -10.4423

, que é a solução de quadrados mínimos do sistema original

Ax = b

. Como esta é solução exata do sistema

\hat{R}x = \hat{c}

, temos que

\|\hat{R}x - \hat{c}\|_2^2 = 0

, logo a soma dos quadrados dos resíduos de

r = Ax-b

, que é igual a dos resíduos de

s = Rx - c

, é calculada apenas com a parte que sobrou do vetor

c

ao extrairmos o vetor

\hat{c}

. Temos:

\|r\|_2^2 \approx 606890

Portanto, obtivemos uma melhor aproximação para os dados da tabela com a expressão:

cal = 49.1001p - 10.4423i

Com isto podemos, por exemplo, determinar a cota aproximada de calorias para um homem de 30 anos com 70 quilos:

cal = 49.1001\times70 - 10.4423\times 30 \approx 3124

ou para um homem de 50 anos e 78 quilos:

cal = 49.1001\times 78 - 10.4423\times 50 \approx 3308

Voltar ao Topo.

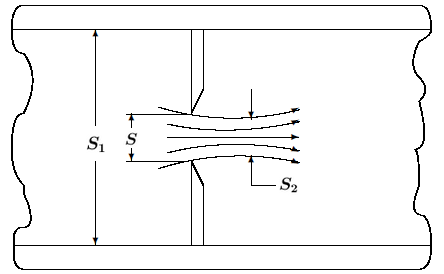
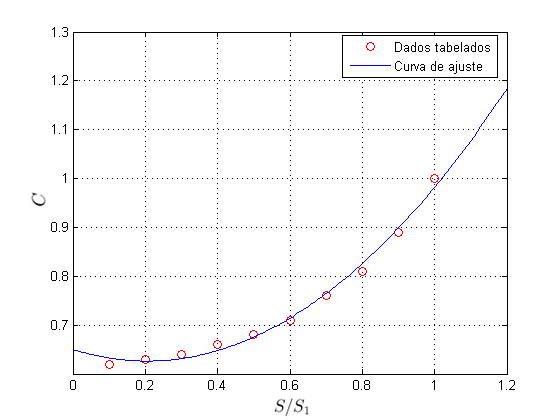
Problema 5 (Placas de Orifício)

Placas de orifício com bordas em canto (ou faca) são muito utilizadas na medição da vazão de fluidos através de tubulações. A figura a seguir mostra uma placa de orifício, que tem os seguintes parâmetros geométricos representativos:

$S$ : área da seção reta do orifício.

$S_1$ : área da seção reta da tubulação.

$S_2 = CS$ : seção reta no ponto de maior contração após o orifício.

O coeficiente

C

é dado em função da razão

S/S_1

, e valores experimentais desse coeficiente estão listados na tabela a seguir:

$S/S_1$	0.10	0.20	0.30	0.40	0.50	0.60	0.70	0.80	0.90	1.00
$C$	0.62	0.63	0.64	0.66	0.68	0.71	0.76	0.81	0.89	1.00

Representando estes dados em um gráfico, temos:

Considerando

x = S/S_1

, vamos ajustar a função

C(x)

por uma função quadrática:

a_0 + a_1x + a_2x^2

, utilizando o método dos quadrados mínimos. Supondo que os dados tabelados satisfazem esta expressão, obtemos o seguinte sistema linear na forma matricial

Av = b

\left[ \begin{array}{ccc} 1 & 0.1 & 0.1^2\\ 1 & 0.2 & 0.2^2\\ 1 & 0.3 & 0.3^2\\ 1 & 0.4 & 0.4^2\\ 1 & 0.5 & 0.5^2\\ 1 & 0.6 & 0.6^2\\ 1 & 0.7 & 0.7^2\\ 1 & 0.8 & 0.8^2\\ 1 & 0.9 & 0.9^2\\ 1 & 1 & 1^2 \end{array} \right] \; \left[ \begin{array}{c} a_0 \\ a_1 \\ a_2 \end{array} \right] = \left[ \begin{array}{ccc} 1 & 0.1 & 0.01\\ 1 & 0.2 & 0.04\\ 1 & 0.3 & 0.09\\ 1 & 0.4 & 0.16\\ 1 & 0.5 & 0.25\\ 1 & 0.6 & 0.36\\ 1 & 0.7 & 0.49\\ 1 & 0.8 & 0.64\\ 1 & 0.9 & 0.81\\ 1 & 1 & 1 \end{array} \right]\; \left[ \begin{array}{c} a_0 \\ a_1 \\ a_2 \end{array} \right] = \left[ \begin{array}{c} 0.62\\ 0.63\\ 0.64\\ 0.66\\ 0.68\\ 0.71\\ 0.76\\ 0.81\\ 0.89\\ 1 \end{array} \right]

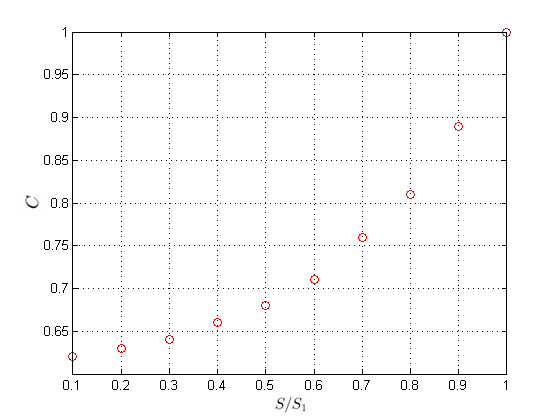
Este sistema é inconsistente e queremos, portanto, obter uma solução que minimize a norma do resíduo

r = Av - b

. Na fatoração ortogonal da matriz

A

dos coeficientes, determinamos a matriz

Q \in \mathbb{R}^{10} \times \mathbb{R}^{10}

ortogonal e a matriz triangular superior:

R = \left[ \begin{array}{rrr} -3.1623 & -1.7393 & -1.2175\\ 0 & 0.9083 & 0.9991\\ 0 & 0 & 0.2298\\ 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array} \right]

tais que

A = QR

. Então

Av = b \Leftrightarrow QRv = b \Leftrightarrow Rv = Q^tb

, pois

Q

é uma matriz ortogonal. Chamando

c = Q^tb

, temos o sistema:

Rv = c \Leftrightarrow \left[ \begin{array}{rrr} -3.1623 & -1.7393 & -1.2175\\ 0 & 0.9083 & 0.9991\\ 0 & 0 & 0.2298\\ 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array} \right] \;\left[ \begin{array}{c} a_0 \\ a_1 \\ a_2 \end{array} \right] = \left[ \begin{array}{r} -2.3401 \\ 0.3534\\ 0.1297\\ 0.0116\\ 0.0038\\ -0.0045\\ -0.0033\\ -0.0126\\ -0.0025\\ 0.0272 \end{array} \right]

Como abaixo da linha 3 a matriz

R

é nula, os valores abaixo da linha 3 de

c

não dependem do vetor

v

no sistema. Podemos então extrair a matriz

\hat{R}

e o vetor

\hat{c}

dados por:

\hat{R} = \left[\begin{array}{rrr} -3.1623 & -1.7393 & -1.2175 \\ 0 & 0.9083 & 0.9991 \\ 0 & 0 & 0.2298 \end{array}\right] \;\;\;\; e \;\;\;\; \hat{c} = \left[ \begin{array}{r} -2.3401 \\ 0.3534 \\ 0.1297 \end{array} \right]

e resolvemos o sistema

\hat{R}v = \hat{c}

\left[\begin{array}{rrr} -3.1623 & -1.7393 & -1.2175 \\ 0 & 0.9083 & 0.9991 \\ 0 & 0 & 0.2298 \end{array}\right] \; \left[ \begin{array}{c} a_0 \\ a_1 \\ a_2 \end{array} \right] = \left[ \begin{array}{r} -2.3401 \\ 0.3534 \\ 0.1297 \end{array} \right]

Este sistema é determinado e apresenta como única solução:

a_0 = 0.6502

a_1 = -0.2317

a_2 = 0.5644

. Temos que

\|\hat{R}v - \hat{c}\|_2^2 = 0

e, portanto, a soma dos quadrados dos resíduos de

r = Av-b

, que é igual a dos resíduos de

s = Rv-c

, é calculada apenas com a parte que sobrou do vetor

c

ao extrairmos o vetor

\hat{c}

. Neste caso, temos:

\|r\|_2^2 = 0.0011

, e esta é a norma mínima. Portanto, com a solução de quadrados mínimos, obtivemos os coeficientes do polinômio de grau 2:

C(x) = 0.6502 - 0.2317x + 0.5644x^2

que melhor ajusta os dados tabelados.

Voltar ao Topo.

Última Atualização: 05/08/2016.