Fatoração QR - Processo de Gram-Schmidt
Página Inicial
ESPAÇOS VETORIAIS
Espaços Vetoriais
Subespaços Vetoriais
Combinação Linear
Subespaços Gerados
Intersecção de Subespaços
Soma de Subespaços
Dependência Linear
Base e Dimensão
Mudança de Base

TRANSFORMAÇÕES LINEARES
Transformações Lineares
Núcleo e Imagem
Teorema do Núcleo e da Imagem
Isomorfismo e Automorfismo
Álgebra das Transformações Lineares
Matriz de uma Transformação

AUTOVALORES E AUTOVETORES
Autovalores e Autovetores
Polinômio Característico
Diagonalização

ESPAÇOS COM PRODUTO INTERNO
Produto Interno
Norma e Distância
Ortogonalidade

DETERMINANTES
Determinantes
Propriedades do Determinante
Cálculo de Determinantes

SISTEMAS LINEARES
Sistemas Lineares
Operações Elementares
Sistemas Triangulares
Eliminação Gaussiana

FATORAÇÕES MATRICIAIS
Fatoração LU
Fatoração de Cholesky
Fatoração Ortogonal
Fatoração QR - Processo de Gram-Schmidt
Fatoração QR - Transformações de Householder

QUADRADOS MÍNIMOS
Método de Quadrados Mínimos
Ajuste de Curvas
Problemas Aplicados

 OUTRAS APLICAÇÕES
Curvas e Superfícies por Pontos Especificados
Criptografia
Jogos de Estratégia
Classificação de Cônicas


Bases ortonormais de um espaço vetorial possuem propriedades importantes e são úteis em diversos problemas. O processo de ortogonalização de Gram-Schmidt é um método utilizado para converter uma conjunto arbitrário de um espaço vetorial em um conjunto ortogonal. É claro que os vetores da base ortogonal podem ser ortonormalizados, produzindo então uma base ortonormal. A construção deste processo mostra um importante resultado de que todo espaço vetorial não nulo de dimensão finita possui uma base ortonormal.

Teorema 1: Sejam VV um espaço vetorial de dimensão finita com produto interno e B={v1,v2,...,vn}B = \left\lbrace v_1, v_2, ..., v_n \right\rbrace um conjunto L.I. de VV. Então, podemos obter um conjunto ortonormal B¯={q1,q2,...,qn}\bar{B} = \left\lbrace q_1, q_2, ..., q_n \right\rbrace de VV. Além disso:

[v1,...,vk]=[q1,...,qk]\left[v_1, ..., v_k \right] = \left[ q_1, ..., q_k \right]
para k=1,...,nk = 1, ..., n, onde Sk=[v1,...,vk]S_k = \left[v_1, ..., v_k \right] e Wk=[q1,...,qk]W_k = \left[ q_1, ..., q_k \right] são os subespaços gerados pelos elementos v1,...,vkv_1, ..., v_k e q1,...,qkq_1, ..., q_k, respectivamente.

Demonstração:
Etapa 1: Sejam S1=[v1]S_1 = \left[ v_1 \right] e W1=[q1]W_1 = \left[ q_1 \right]. Para satisfazer S1=W1S_1 = W_1 basta escolher q1q_1 como sendo um múltiplo de v1v_1. Como também queremos ‖q1‖=1\left\| q_1 \right\| = 1, escolhemos q1q_1 como sendo o elemento v1v_1 normalizado:

q1=v1r11q_1 = \frac{v_1}{r_{11}}
onde r11=‖v1‖r_{11} = \left\| v_1 \right\|. Sabemos que r11>0r_{11} > 0, uma vez que os vetores v1,...,vnv_1, ..., v_n são linearmente independentes e, portanto, v1≠eVv_1 \neq e_V. Como q1q_1 é múltiplo de v1v_1, segue que q1∊S1q_1 \in S_1 e logo W1⊆S1W_1 \subseteq S_1. Reciprocamente, como v1=r11q1v_1 = r_{11}q_1 segue que v1∊W1v_1 \in W_1 e logo S1⊆W1S_1 \subseteq W_1. Portanto, S1=W1S_1 = W_1.

Etapa 2: O subespaço S2=[v1,v2]S_2 = \left[v_1, v_2\right] gerado por v1v_1 e v2v_2 é um plano. Queremos encontrar um elemento q2q_2 ortogonal a q1q_1 tal que o subespaço W2=[q1,q2]W_2 = \left[ q_1, q_2 \right] também é este mesmo plano, isto é, S2=W2S_2 = W_2. Sabemos que q1q_1 é o vetor v1v_1 normalizado e que v2v_2 não é múltiplo de v1v_1 pois eles são linearmente independentes. Podemos então encontrar um múltiplo r12r_{12} adequado de q1q_1 e obter um elemento q2^=v2-r12q1\hat{q_2} = v_2 - r_{12}q_1, conforme exemplificamos na Figura 1:

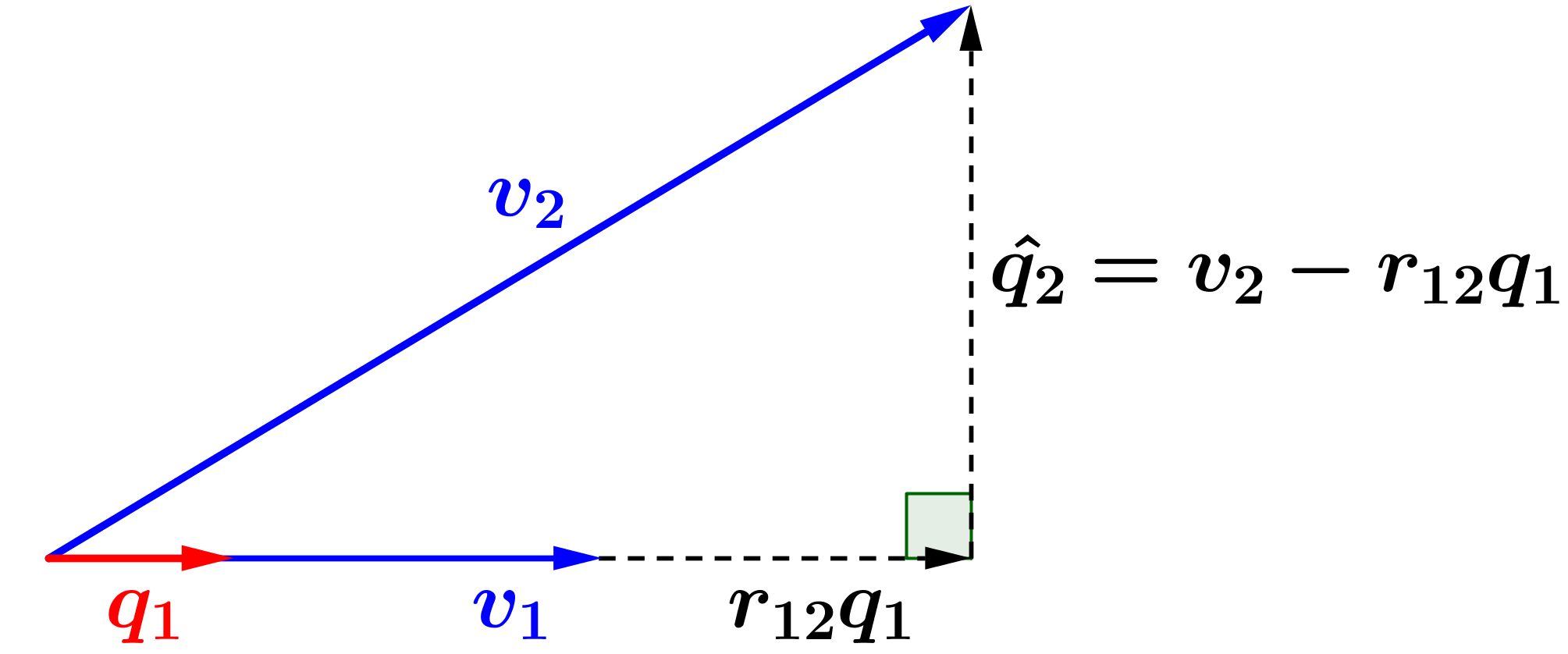
ex1_gram
  Figura 1: Construção do vetor q2^\hat{q_2}.

Tomando o produto interno com q1q_1 em ambos os termos da equação que determina q2^\hat{q_2}, temos:

q2^=v2-r12q1⇒⟨q2^,q1⟩=⟨v2,q1⟩-⟨r12q1,q1⟩⇒⟨q2^,q1⟩=⟨v2,q1⟩-r12⟨q1,q1⟩\hat{q_2} = v_2 - r_{12}q_1 \Rightarrow \langle \hat{q_2}, q_1 \rangle = \langle v_2, q_1 \rangle - \langle r_{12}q_1, q_1\rangle \Rightarrow \langle \hat{q_2}, q_1 \rangle = \langle v_2, q_1 \rangle - r_{12}\langle q_1, q_1\rangle
Como queremos q2^\hat{q_2} ortogonal a q1q_1, isto é, ⟨q2^,q1⟩=0\langle \hat{q_2}, q_1 \rangle = 0 e temos ⟨q1,q1⟩=‖q1‖2=1\langle q_1, q_1\rangle = \left\| q_1 \right\|^2 = 1, a equação acima se reduz a:

0=⟨v2,q1⟩-r12⇔r12=⟨v2,q1⟩0 = \langle v_2, q_1 \rangle - r_{12} \Leftrightarrow r_{12} = \langle v_2, q_1 \rangle
Então, considerando r12=⟨v2,q1⟩r_{12} = \langle v_2, q_1 \rangle obtemos q2^=v2-r12q1\hat{q_2} = v_2 - r_{12}q_1 e temos ⟨q2^,q1⟩=0\langle \hat{q_2}, q_1 \rangle = 0. É claro que q2^≠eV\hat{q_2} \neq e_V, pois se isso acontecesse teríamos v2=r12q1v_2 = r_{12}q_1 e então v2∊[q1]=[v1]v_2 \in [q_1] = [v_1], o que não pode ocorrer devido a independência linear entre v1v_1 e v2v_2. Agora, para obtermos q2q_2 ortogonal a q1q_1 e tal que ‖q2‖=1\left\| q_2 \right\| = 1, escolhemos q2q_2 como sendo o elemento q2^\hat{q_2} normalizado:
 q2=q2^r22q_2 = \frac{\hat{q_2}}{r_{22}}
onde r22=‖q2^‖>0r_{22} = \left\| \hat{q_2} \right\| > 0. Vamos mostrar agora que S2=W2S_2 = W_2. Temos que q1∊[v1]⊆[v1,v2]=S2q_1 \in \left[ v_1 \right] \subseteq \left[ v_1, v_2 \right] = S_2 e q2∊[q1,v2]=[v1,v2]=S2q_2 \in \left[q_1, v_2 \right] = \left[ v_1, v_2 \right] = S_2. Uma vez que q1,q2∊S2q_1, q_2 \in S_2 temos W2⊆S2W_2 \subseteq S_2. Reciprocamente, temos que v1∊[q1]⊆[q1,q2]=W2v_1 \in \left[ q_1 \right] \subseteq \left[ q_1, q_2 \right] = W_2 e v2=r12q1+q2^=r12q1+r22q2v_2 = r_{12}q_1 + \hat{q_{2}} = r_{12}q_1 + r_{22}q_2, logo v2∊[q1,q2]=W2v_2 \in \left[q_1, q_2 \right] = W_2. Uma vez que v1,v2∊W2v_1, v_2 \in W_2 temos S2⊆W2S_2 \subseteq W_2. Portanto, S2=W2S_2 = W_2.

Seguimos com a mesma ideia nas etapas 3,4,...,n3, 4, ..., n. Por indução, suponha que encontramos elementos q1,q2,...,qk-1q_1, q_2, ..., q_{k-1} ortonormais, tais que [v1,...,vi]=[q1,...,qi]\left[ v_1, ..., v_i \right] = \left[ q_1, ..., q_i \right] para i=1,2,...,k-1i = 1, 2, ..., k-1.

Etapa k: Seja Sk=[v1,...,vk]S_k = \left[ v_1, ..., v_k\right] o subespaço gerado por v1,...,vkv_1, ..., v_k. Queremos encontrar um elemento qkq_k com norma igual a 1, ortogonal a q1,...,qk-1q_1, ..., q_{k-1} e tal que Wk=[q1,...,qk]=SkW_k = \left[ q_1, ..., q_k\right] = S_k. Considere:

qk^=vk-∑j=1k-1rjkqj\hat{q_k} = v_k - \sum_{j=1}^{k-1} r_{jk} q_j
Para determinar os múltiplos rikr_{ik}, para i=1,...,k-1i = 1, ..., k-1, tomamos o produto interno com qiq_i, obtendo:

⟨qk^,qi⟩=⟨vk,qi⟩-∑j=1k-1rjk⟨qj,qi⟩,i=1,...,k-1\langle \hat{q_k}, q_i \rangle = \langle v_k, q_i \rangle - \sum_{j=1}^{k-1}r_{jk} \langle q_j, q_i \rangle, \;\;\;\;\;\; i = 1, ..., k-1
Como queremos qk^\hat{q_k} ortogonal a qiq_i, temos que ter ⟨qk^,qi⟩=0\langle \hat{q_k}, q_i \rangle = 0, para i=1,...,k-1i = 1, ..., k-1 e além disso, temos ⟨qi,qi⟩=‖qi‖2=1\langle q_i, q_i \rangle = \left\| q_i \right\|^2 = 1 e ⟨qj,qi⟩=0\langle q_j, q_i \rangle = 0, para j≠ij \neq i. Assim, as equações acima se reduzem a:

0=⟨vk,qi⟩-rik⇔rik=⟨vk,qi⟩0 = \langle v_k, q_i \rangle - r_{ik} \Leftrightarrow r_{ik} = \langle v_k, q_i \rangle
Dessa forma, considerando rik=⟨vk,qi⟩r_{ik} = \langle v_k, q_i \rangle, para i=1,...,k-1i = 1, ..., k-1 obtemos qk^\hat{q_k} ortogonal a q1,...,qk-1q_1, ..., q_{k-1}. É claro que qk^≠eV\hat{q_k} \neq e_Vqk^≠eV\hat{q_k} \neq e_V, pois se isso acontecesse teríamos vk∊[q1,...,qk-1]=[v1,...,vk-1]v_k \in \left[q_1, ..., q_{k-1} \right] = \left[ v_1, ..., v_{k-1} \right], o que não pode ocorrer devido a independência linear de v1,...,vkv_1, ..., v_k. Agora, para obtermos qkq_k ortogonal a q1,...,qk-1q_1, ..., q_{k-1} e tal que ‖qk‖=1\left\| q_k\right\| = 1, escolhemos qkq_k como sendo o elemento qk^\hat{q_k} normalizado:

qk=qk^rkkq_k = \frac{\hat{q_k}}{r_{kk}}
onde rkk=‖qk^‖>0r_{kk} = \left\|\hat{q_k} \right\| > 0. Vamos mostrar agora que Sk=WkS_k = W_k. Temos que qi∊Wk-1=Sk-1⊆Skq_i \in W_{k-1} = S_{k-1} \subseteq S_k para i=1,...,k-1i = 1, ..., k-1 e qk∊[q1,...,qk-1,vk]=[v1,...,vk-1,vk]=Skq_k \in \left[ q_1, ..., q_{k-1}, v_k \right] = \left[v_1, ..., v_{k-1}, v_k\right] = S_k. Uma vez que q1,...,qk∊Skq_1, ..., q_k \in S_k temos Wk⊆SkW_k \subseteq S_k. Reciprocamente, temos que vi∊Sk-1=Wk-1⊆Wkv_i \in S_{k-1} = W_{k-1} \subseteq W_k para i=1,...,k-1i = 1, ..., k-1 e como vk=∑j=1krjkqjv_k = \sum_{j=1}^{k}r_{jk}q_j temos que vk∊[q1,...,qk]=Wkv_k \in \left[q_1, ..., q_k \right] = W_k. Uma vez que v1,...,vk∊Wkv_1, ..., v_k \in W_k temos Sk⊆WkS_k \subseteq W_k. Portanto, Sk=WkS_k = W_k.

Quando chegarmos no final da etapa nn, teremos obtido elementos q1,...,qnq_1, ..., q_n ortonormais e tais que [q1,...,qk]=[v1,...,vk]\left[ q_1, ..., q_k\right] = \left[ v_1, ..., v_k\right], para k=1,...,nk = 1, ..., n. Assim, se o conjunto B={v1,...,vn}B = \left\lbrace v_1, ..., v_n\right\rbrace for uma base para o espaço VV, temos que o conjunto B¯={q1,...,qn}\bar{B} = \left\lbrace q_1, ..., q_n\right\rbrace forma uma base ortonormal para VV.


Exemplo 1: Considere o espaço vetorial real R3R^3 com produto interno Euclidiano e uma base B={v1=(0,0,1),v2=(1,0,-1),v3=(0,1,1)}B = \left\lbrace v_1 = (0, 0, 1), v_2 = (1, 0, -1), v_3 = (0, 1, 1)\right\rbrace para o R3R^3. Vamos obter uma base ortonormal B¯={q1,q2,q3}\bar{B} = \left\lbrace q_1, q_2, q_3\right\rbrace  para o R3R^3 usando o processo de ortogonalização de Gram-Schmidt.

Etapa 1: Escolhemos q1q_1 como sendo o elemento v1v_1 normalizado:

q1=v1‖v1‖2=v1=(0,0,1)q_1 = \frac{v_1}{\left\| v_1\right\|_2} = v_1 = (0, 0, 1)
Etapa 2: Consideramos o elemento q2^\hat{q_2} ortogonal à q1q_1 da forma:

q2^=v2-⟨v2,q1⟩q1=(1,0,-1)-(-1)(0,0,1)=(1,0,0)\hat{q_2} = v_2 - \langle v_2, q_1\rangle q_1 = (1, 0, -1) - (-1)(0, 0, 1) = (1, 0, 0)
Temos que ⟨q1,q2^⟩=⟨(0,0,1),(1,0,0)⟩=0\langle q_1, \hat{q_2}\rangle = \langle (0, 0, 1), (1, 0, 0)\rangle = 0 e, portanto, q1q_1 e q2^\hat{q_2} são ortogonais. Para que ‖q2‖2=1\left\| q_2\right\|_2 = 1, escolhermos q2q_2 como sendo o elemento q2^\hat{q_2} normalizado:

q2=q2^‖q2^‖2=q2^=(1,0,0)q_2 = \frac{\hat{q_2}}{\left\| \hat{q_2}\right\|_2} = \hat{q_2} = (1, 0, 0)
Etapa 3: Consideramos o elemento q3^\hat{q_3} ortogonal a q1q_1 e q2q_2 da forma:

q3^=v3-⟨v3,q1⟩q1-⟨v3,q2⟩q2=(0,1,1)-1(0,0,1)-0(1,0,0)=(0,1,0) \hat{q_3} = v_3 - \langle v_3, q_1\rangle q_1 - \langle v_3, q_2\rangle q_2 = (0, 1, 1) - 1(0, 0, 1) - 0(1, 0, 0) = (0, 1, 0)
Temos que ⟨q1,q3^⟩=⟨(0,0,1),(0,1,0)⟩=0\langle q_1, \hat{q_3}\rangle = \langle (0, 0, 1), (0, 1, 0)\rangle = 0 e ⟨q2,q3^⟩=⟨(1,0,0),(0,1,0)⟩=0\langle q_2, \hat{q_3}\rangle = \langle (1, 0, 0), (0, 1, 0)\rangle = 0 e, portanto, q1,q2q_1, q_2 e q3^\hat{q_3} são ortogonais. Para que ‖q3‖2=1\left\| q_3\right\|_2 = 1, escolhemos q3q_3 como sendo o elementos q3^\hat{q_3} normalizado:

q3=q3^‖q3^‖2=q3^=(0,1,0)q_3 = \frac{\hat{q_3}}{\left\| \hat{q_3}\right\|_2} = \hat{q_3} = (0, 1, 0)
Portanto, obtemos o conjunto B¯={q1=(0,0,1),q2=(1,0,0),q3=(0,1,0)}\bar{B} = \left\lbrace q_1 = (0, 0, 1), q_2 = (1, 0, 0), q_3 = (0, 1, 0) \right\rbrace que é a base canônica do R3R^3 e de fato é uma base ortonormal.


Algoritmo (Processo de Gram-Schmidt): Sejam v1,v2,...,vnv_1, v_2, ..., v_n elementos linearmente independentes de um espaço vetorial VV com produto interno. Podemos obter elementos q1,...,qnq_1, ..., q_n ortonormais de VV, tais que [q1,...,qk]=[v1,...,vk]\left[ q_1, ..., q_k\right] = \left[v_1, ..., v_k \right] para k=1,...,nk = 1, ..., n, através do seguinte algoritmo:
Algoritmo.


Voltar ao Topo.

Fatoração QR através do Processo de Gram-Schmidt

Seja A∊Rn×RnA \in R^n \times R^n uma matriz com colunas linearmente independentes. Isto é, os vetores coluna a1,a2,...,ana_1, a_2, ..., a_n são linearmente independentes. Então, podemos utilizar o processo de ortogonalização de Gram-Schmidt no conjunto B={a1,...,an}B = \left\lbrace a_1, ..., a_n\right\rbrace, obtendo elementos não nulos e ortogonais qk^\hat{q_k}, da forma:

qk^=ak-∑j=1k-1rjkqj,k=1,...,n(1)\hat{q_k} = a_k - \sum_{j=1}^{k-1}r_{jk}q_j, \;\;\;\;\;\; k = 1, ..., n \;\;\;\;\;\;\;\;\;\;\;\; (1)
onde rik=⟨vk,qi⟩r_{ik} = \langle v_k, q_i\rangle, para i=1,...,k-1i = 1, ..., k-1. Além disso, obtemos vetores ortonormais qkq_k, normalizando os vetores qk^\hat{q_k}, da seguinte forma:

qk=qk^rkk,k=1,...,n(2)q_k = \frac{\hat{q_k}}{r_{kk}}, \;\;\;\;\;\; k = 1, ..., n \;\;\;\;\;\;\;\;\;\;\;\;\; (2)
onde rkk=‖qk^‖2>0r_{kk} = \left\| \hat{q_k} \right\|_2 > 0. Juntando as equações (1)(1) e (2)(2), obtemos:

ak=∑j=1k-1rjkqj+rkkqk,k=1,...,na_k = \sum_{j=1}^{k-1}r_{jk}q_j + r_{kk}q_k, \;\;\;\;\;\; k = 1, ..., n
Ou então:
a1=q1r11a2=q1r12+q2r22⋮an=q1r1n+q2r2n+...+qnrnn\begin{array}{lcl} a_1 & = & q_1 r_{11} \\ a_2 & = & q_1 r_{12} + q_2 r_{22} \\ & \vdots & \\ a_n & = & q_1 r_{1n} + q_2 r_{2n} + ... + q_n r_{nn} \end{array}
Estas equações podem ser escritas como um produto matricial:

[a1a2⋯an]=[q1q2⋯qn][r11r12⋯r1n0r22⋯r2n⋮⋮⋱⋮00⋯rnn]⇔A=QR\left[ \begin{array}{cccc} a_1 & a_2 & \cdots & a_n \end{array}\right] = \left[ \begin{array}{cccc} q_1 & q_2 & \cdots & q_n \end{array}\right] \;\left[ \begin{array}{cccc} r_{11} & r_{12} & \cdots & r_{1n} \\ 0 & r_{22} & \cdots & r_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & r_{nn} \end{array}\right] \Leftrightarrow A = QR
Note que a matriz QQ é ortogonal, pois suas colunas são vetores ortonormais e RR é uma matriz triangular superior com diagonal positiva. Assim, obtemos a fatoração ortogonal A=QRA = QR da matriz AA.


Exemplo 2: Considere a seguinte matriz:
A=[102011120]A = \left[ \begin{array}{ccc} 1 & 0 & 2 \\ 0 & 1 & 1 \\ 1 & 2 & 0 \end{array}\right]
Vamos encontrar a fatoração QRQR de AA utilizando o processo de ortogonalização de Gram-Schmidt nos vetores coluna de AA. Sabemos que os vetores a1=(1,0,1)t,a2=(0,1,2)ta_1 = (1, 0, 1)^t, a_2 = (0, 1, 2)^t e a3=(2,1,0)ta_3 = (2, 1, 0)^t são linearmente independentes. Considerando r11=‖a1‖2=12+12=2r_{11} = \left\| a_1 \right\|_2 = \sqrt{1^2 + 1^2} = \sqrt{2}, obtemos:

q1=a1r11⇒q1=[1/201/2]q_1 = \frac{a_1}{r_{11}} \Rightarrow q_1 = \left[ \begin{array}{c} 1/\sqrt{2} \\ 0 \\ 1 / \sqrt{2} \end{array}\right]
Consideramos r12=⟨a2,q1⟩=22r_{12} = \langle a_2, q_1 \rangle = \frac{2}{\sqrt{2}} e obtemos o elemento q2^\hat{q_2} ortogonal a q1q_1 da forma:

q2^=a2-r12q1=[012]-22[1/201/2]=[012]-[101]=[-111]\hat{q_2} = a_2 - r_{12}q_1 = \left[ \begin{array}{c} 0 \\ 1 \\ 2 \end{array}\right] - \frac{2}{\sqrt{2}}\left[ \begin{array}{c} 1/\sqrt{2} \\ 0 \\ 1/\sqrt{2} \end{array}\right] = \left[ \begin{array}{c} 0 \\ 1 \\ 2 \end{array}\right] - \left[ \begin{array}{c} 1 \\ 0 \\ 1 \end{array}\right] = \left[ \begin{array}{r} -1 \\ 1 \\ 1 \end{array}\right]
Tomando r22=‖q2^‖2=3r_{22} = \left\| \hat{q_2} \right\|_2 = \sqrt{3}, temos:

q2=q2^r22=[-1/31/31/3]q_2 = \frac{\hat{q_2}}{r_{22}} = \left[ \begin{array}{r} -1/\sqrt{3} \\ 1/\sqrt{3} \\ 1/\sqrt{3} \end{array}\right]
Consideramos r13=⟨a3,q1⟩=22r_{13} = \langle a_3, q_1 \rangle = \frac{2}{\sqrt{2}} e r23=⟨a3,q2⟩=-13r_{23} = \langle a_3, q_2 \rangle = -\frac{1}{\sqrt{3}} e obtemos q3^\hat{q_3} ortogonal a q1q_1 e q2q_2 da forma:

q3^=a3-r13q1-r23q2=[210]-22[1/201/2]+13[-1/31/31/3]=[2/34/3-2/3]\hat{q_3} = a_3 - r_{13}q_1 - r_{23}q_2 = \left[ \begin{array}{r} 2 \\ 1 \\ 0 \end{array}\right] - \frac{2}{\sqrt{2}} \left[ \begin{array}{c} 1/\sqrt{2} \\ 0 \\ 1/\sqrt{2} \end{array}\right] + \frac{1}{\sqrt{3}} \left[ \begin{array}{r} -1/\sqrt{3} \\ 1/\sqrt{3} \\ 1/\sqrt{3} \end{array}\right] = \left[ \begin{array}{r} 2/3 \\ 4/3 \\ -2/3 \end{array}\right]
Tomando r33=‖q3^‖2=243=263r_{33} = \left\| \hat{q_3}\right\|_2 = \frac{\sqrt{24}}{3} = \frac{2\sqrt{6}}{3}, temos:
q3=q3^r33=[1/62/6-1/6]q_3 = \frac{\hat{q_3}}{r_{33}} = \left[ \begin{array}{r} 1/\sqrt{6} \\ 2/\sqrt{6} \\ -1/\sqrt{6} \end{array}\right]
Portanto, temos a fatoração:
A=QR⇔[a1a2a3]=[q1q2q3][r11r12r130r12r2300r33]⇔A = QR \Leftrightarrow \left[ \begin{array}{ccc} a_1 & a_2 & a_3 \end{array}\right] = \left[ \begin{array}{ccc} q_1 & q_2 & q_3 \end{array}\right] \;\left[ \begin{array}{ccc} r_{11} & r_{12} & r_{13} \\ 0 & r_{12} & r_{23} \\ 0 & 0 & r_{33} \end{array}\right] \Leftrightarrow
⇔[102011120]=[1/2-1/31/601/32/61/21/3-1/6][22/22/203-1/30024/3]\Leftrightarrow \left[ \begin{array}{ccc} 1 & 0 & 2 \\ 0 & 1 & 1 \\ 1 & 2 & 0 \end{array}\right] = \left[ \begin{array}{crr} 1/\sqrt{2} & -1/\sqrt{3} & 1/\sqrt{6} \\ 0 & 1/\sqrt{3} & 2/\sqrt{6} \\ 1/\sqrt{2} & 1/\sqrt{3} & -1/\sqrt{6} \end{array}\right] \;\left[ \begin{array}{ccr} \sqrt{2} & 2/\sqrt{2} & 2/\sqrt{2} \\ 0 & \sqrt{3} & -1/\sqrt{3} \\ 0 & 0 & \sqrt{24}/3 \end{array}\right]
Observe que a matriz QQ é ortogonal e RR é triangular superior com elementos da diagonal positivos.


Voltar ao Topo.

Resolução de Sistemas Lineares Utilizando a Fatoração QR

Considere o sistema linear Ax=bAx = b em que A:n×nA: n \times n é uma matriz não singular. Então, podemos obter uma matriz Q:n×nQ:n \times n ortogonal e uma matriz R:n×nR: n \times n triangular superior, tais que A=QRA = QR. Então:

Ax=b⇔(QR)x=b⇔Rx=QtbAx = b \Leftrightarrow (QR)x = b \Leftrightarrow Rx = Q^tb
uma vez que QtQ=InQ^tQ = I_n. Assim, a solução do sistema linear Ax=bAx = b pode ser obtida seguindo os passos:

    (i) Obter a fatoração ortogonal A=QRA = QR;
    (ii) Obter o vetor b¯=Qtb\bar{b} = Q^tb;
    (iii) Resolver o sistema triangular superior Rx=b¯Rx = \bar{b}.

Exemplo 3: Considere o seguinte sistema linear na forma matricial:

Ax=b⇔[1213][x1x2]=[12]Ax = b \Leftrightarrow \left[ \begin{array}{cc} 1 & 2 \\ 1 & 3 \end{array} \right]\; \left[ \begin{array}{c} x_1 \\ x_2 \end{array} \right] = \left[ \begin{array}{c} 1 \\ 2 \end{array} \right]
Vamos resolver o sistema utilizando a fatoração QRQR da matriz AA. Os vetores coluna a1a_1 e a2a_2 de AA são linearmente independentes. Pelo processo de Gram-Schmidt, tomamos r11=‖a1‖2=2r_{11} = \left\| a_1 \right\|_2 = \sqrt{2} e normalizamos o vetor a1a_1, obtendo:

q1=a1r11=12[11]q_1 = \frac{a_1}{r_{11}} = \frac{1}{\sqrt{2}}\left[ \begin{array}{c} 1 \\ 1 \end{array} \right]
Agora, consideramos r12=⟨a2,q1⟩=52r_{12} = \langle a_2, q_1 \rangle = \frac{5}{\sqrt{2}} e definimos o vetor q2^\hat{q_2} ortogonal a q1q_1 da seguinte forma:

q2^=a2-r12q1=[23]-52[11]=12[-11]\hat{q_2} = a_2 - r_{12}q_1 = \left[ \begin{array}{c} 2 \\ 3 \end{array} \right] - \frac{5}{2} \left[ \begin{array}{c} 1 \\ 1 \end{array} \right] = \frac{1}{2}\left[ \begin{array}{r} -1 \\ 1 \end{array} \right]
Então, tomamos r22=‖q2^‖2=12r_{22} = \left\| \hat{q_2} \right\|_2 = \frac{1}{\sqrt{2}} e normalizamos o vetor q2^\hat{q_2}, obtendo:

q2=q2^r22=12[-11]q_2 = \frac{\hat{q_2}}{r_{22}} = \frac{1}{\sqrt{2}} \left[ \begin{array}{r} -1 \\ 1 \end{array} \right]
Portanto, obtemos as matrizes:

Q=12[1-111],R=12[2501]Q = \frac{1}{\sqrt{2}} \left[ \begin{array}{rr} 1 & -1 \\ 1 & 1 \end{array} \right], \;\;\;\;\;\;\;\; R = \frac{1}{\sqrt{2}} \left[ \begin{array}{rr} 2 & 5 \\ 0 & 1 \end{array} \right]
onde QQ é ortogonal e RR é triangular superior, tais que A=QRA = QR. Resolvendo b¯=Qtb\bar{b} = Q^tb, temos:

b¯=Qtb=12[11-11][12]⇔b¯=12[31]\bar{b} = Q^tb = \frac{1}{\sqrt{2}} \left[ \begin{array}{rr} 1 & 1 \\ -1 & 1 \end{array} \right] \;\left[ \begin{array}{c} 1 \\ 2 \end{array} \right] \Leftrightarrow \bar{b} = \frac{1}{\sqrt{2}} \left[ \begin{array}{c} 3 \\ 1 \end{array} \right]
Por fim, resolvendo o sistema triangular superior Rx=b¯Rx = \bar{b}, obtemos:

Rx=b¯⇔12[2501][x1x2]=12[31]⇔[2501][x1x2]=[31]⇔Rx = \bar{b} \Leftrightarrow \frac{1}{\sqrt{2}} \left[ \begin{array}{rr} 2 & 5 \\ 0 & 1 \end{array} \right] \;\left[ \begin{array}{c} x_1 \\ x_2 \end{array} \right] = \frac{1}{\sqrt{2}} \left[ \begin{array}{c} 3 \\ 1 \end{array} \right] \Leftrightarrow \left[ \begin{array}{rr} 2 & 5 \\ 0 & 1 \end{array} \right] \;\left[ \begin{array}{c} x_1 \\ x_2 \end{array} \right] = \left[ \begin{array}{c} 3 \\ 1 \end{array} \right] \Leftrightarrow
⇔{2x1+5x2=31x2=1⇒{x1=-1x2=1\Leftrightarrow \left\lbrace \begin{array}{ccccc} 2x_1 & + & 5x_2 & = & 3 \\ & & 1x_2 & = & 1 \end{array}\right. \Rightarrow \left\lbrace \begin{array}{ccr} x_1 & = & -1 \\ x_2 & = & 1 \end{array}\right.
Portanto, a solução do sistema linear original é (x1,x2)=(-1,1)(x_1, x_2) = (-1, 1).


Voltar ao Topo.
Última Atualização: 02/02/2016.