Fatoração QR - Transformações de Householder
Página Inicial
ESPAÇOS VETORIAIS
Espaços Vetoriais
Subespaços Vetoriais
Combinação Linear
Subespaços Gerados
Intersecção de Subespaços
Soma de Subespaços
Dependência Linear
Base e Dimensão
Mudança de Base

TRANSFORMAÇÕES LINEARES
Transformações Lineares
Núcleo e Imagem
Teorema do Núcleo e da Imagem
Isomorfismo e Automorfismo
Álgebra das Transformações Lineares
Matriz de uma Transformação

AUTOVALORES E AUTOVETORES
Autovalores e Autovetores
Polinômio Característico
Diagonalização

ESPAÇOS COM PRODUTO INTERNO
Produto Interno
Norma e Distância
Ortogonalidade

DETERMINANTES
Determinantes
Propriedades do Determinante
Cálculo de Determinantes

SISTEMAS LINEARES
Sistemas Lineares
Operações Elementares
Sistemas Triangulares
Eliminação Gaussiana

FATORAÇÕES MATRICIAIS
Fatoração LU
Fatoração de Cholesky
Fatoração Ortogonal
Fatoração QR - Processo de Gram-Schmidt
Fatoração QR - Transformações de Householder

QUADRADOS MÍNIMOS
Método de Quadrados Mínimos
Ajuste de Curvas
Problemas Aplicados

 OUTRAS APLICAÇÕES
Curvas e Superfícies por Pontos Especificados
Criptografia
Jogos de Estratégia
Classificação de Cônicas



Seja u∊Rnu \in R^n um vetor e suponha que queremos transformar uu em um vetor vv, de modo que ‖u‖2=‖v‖2\left\| u \right\|_2 = \left\| v \right\|_2, onde vv é obtido pela equação:

v=Quv = Qu
sendo QQ uma matriz quadrada.

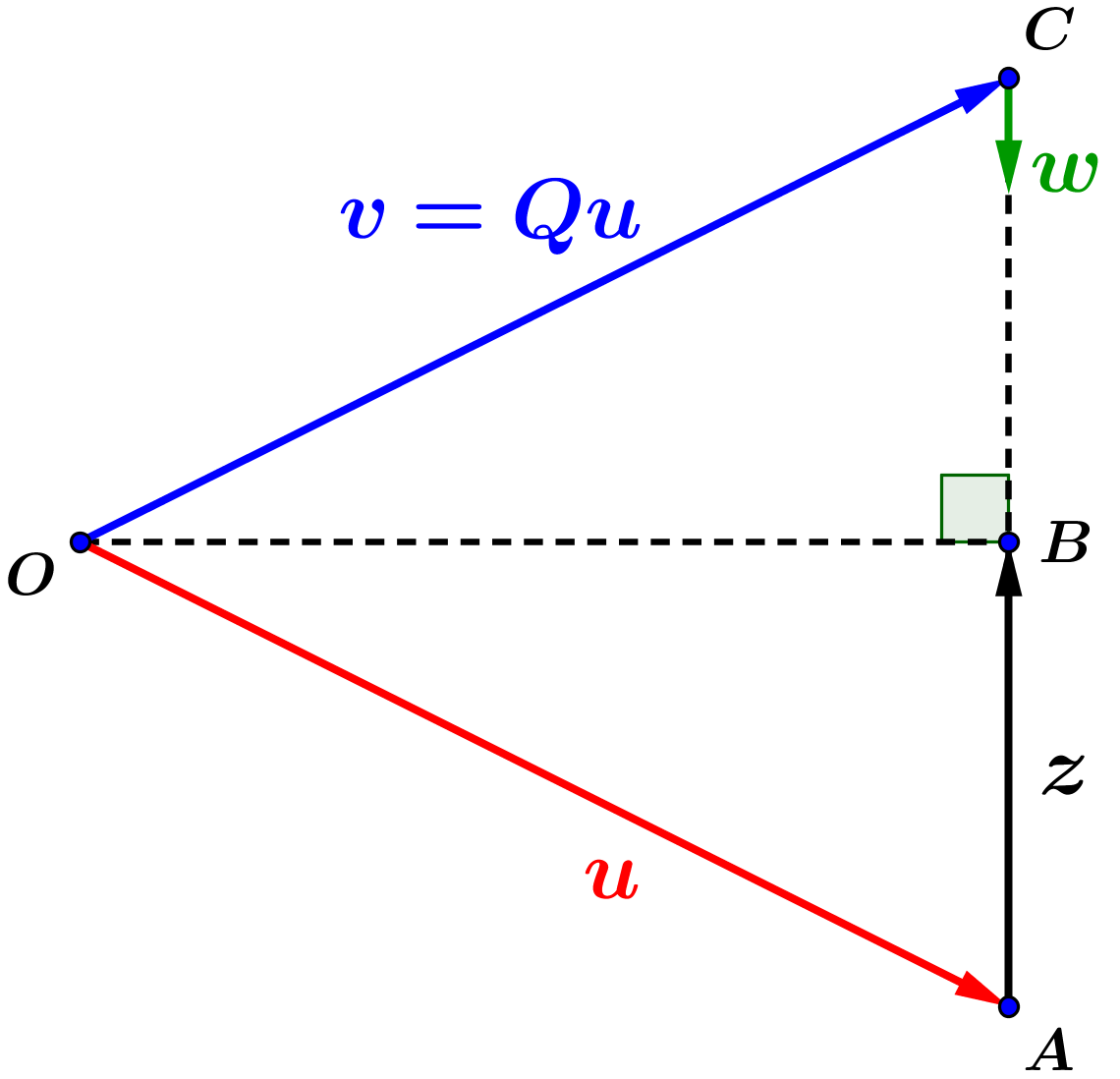
Como queremos que os comprimentos dos vetores uu e vv sejam iguais, considere no plano gerado por u=OAu = OA e v=OCv = OC o triângulo isósceles AOCAOC cujos lados iguais são os segmentos OA¯ \overline{OA} e OC¯\overline{OC}, conforme a Figura 1:
ex1_householder
Figura 1: Interpretação geométrica da transformação linear que leva uu em v:v=Quv: v = Qu.

Queremos encontrar a matriz QQ que realiza a transformação de uu em v:v=Quv: v = Qu. Considerando B o ponto médio do segmento AC¯\overline{AC}, como o triângulo AOCAOC é isósceles temos que OBOB é perpendicular à ACAC. Assim, o vetor z=ABz = AB é o oposto da projeção de OAOA sobre ACAC. Do triângulo AOCAOC extraímos a seguinte relação:

OC=OA+2ABOC = OA + 2 AB
Isto é,

v=u+2z⇔-2z=u-vv = u + 2z \Leftrightarrow -2z = u-v
Seja:
w=u-v‖u-v‖2w = \frac{u-v}{\left\| u-v\right\|_2}
um vetor de norma 1 ao longo de CACA. A projeção de uu sobre ACAC é dada por ‖z‖2w\left\| z\right\|_2w e, portanto, temos:

v=u+2z⇔v=u-2‖z‖2w(1)v = u + 2z \Leftrightarrow v = u - 2\left\| z \right\|_2 w \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(1)

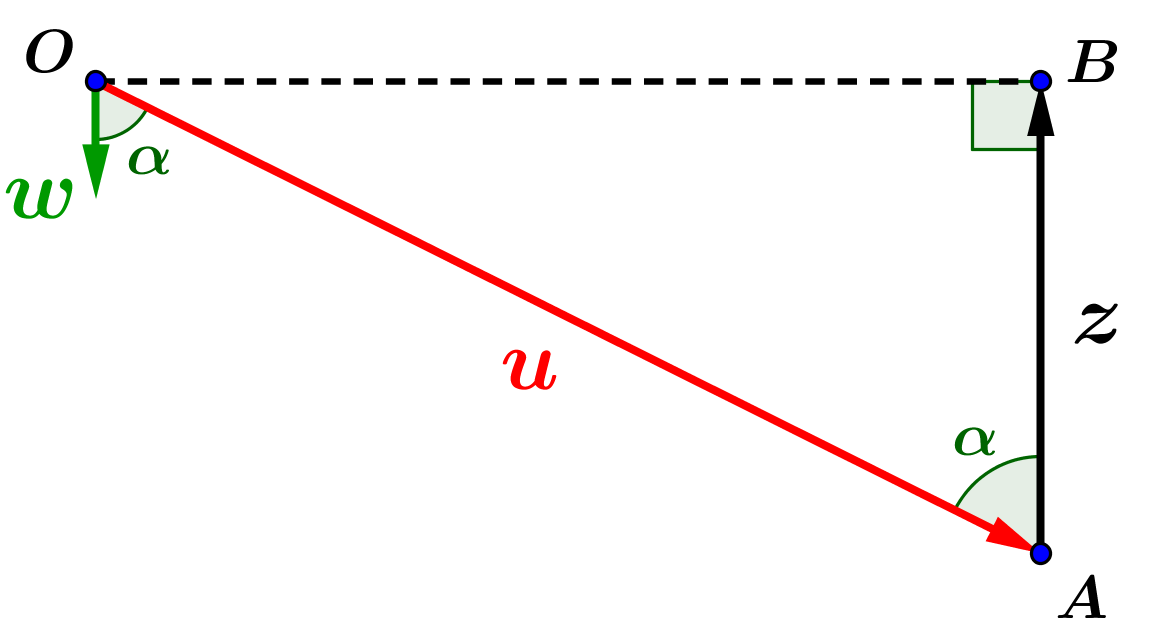
Analisando agora o triângulo retângulo AOBAOB:
ex2_householder
Figura 2: Triângulo AOB.

Note que o ângulo α=BA^O\alpha = B\hat{A}O é o mesmo ângulo entre os vetores uu e ww. Por trigonometria no triângulo retângulo AOBAOB, temos:

cos(α)=‖z‖2‖u‖2⇔‖z‖2=‖u‖2cos(α)\cos(\alpha) = \frac{\left\|z\right\|_2}{\left\|u\right\|_2} \Leftrightarrow \left\| z\right\|_2 = \left\|u\right\|_2 \cos(\alpha)
Mas, como α\alpha também é o ângulo entre uu e ww, por definição temos:

cos(α)=⟨u,w⟩‖u‖2‖w‖2\cos(\alpha) = \frac{\langle u, w \rangle}{\left\|u\right\|_2\left\|w\right\|_2}
Então, obtemos:

‖z‖2=‖u‖2⟨u,w⟩‖u‖2‖w‖2⇒‖z‖2=⟨u,w⟩\left\|z\right\|_2 = \left\|u\right\|_2 \frac{\langle u, w \rangle}{\left\|u\right\|_2\left\|w\right\|_2} \Rightarrow \left\|z\right\|_2 = \langle u, w \rangle
uma vez que ‖w‖2=1\left\|w\right\|_2 = 1. Substituíndo na equação (1)(1), temos:

v=u-2(‖z‖2w)=u-2(⟨u,w⟩w)=u-2(w⟨u,w⟩)=u-2wwtu⇔v = u - 2 \left( \left\|z\right\|_2 w\right) = u - 2\left( \langle u, w \rangle w\right) = u - 2\left( w \langle u, w \rangle\right) = u - 2ww^tu \Leftrightarrow
⇔v=(In-2wwt)u\Leftrightarrow v = \left( I_n - 2ww^t\right) u
Portanto, encontramos a matriz QQ que determina a transformação:

Q=In-2wwtQ = I_n - 2ww^t
denominada matriz de Householder. Observe que a matriz QQ depende somente do vetor ww, isto é, da direção u-vu-v. Então, para quaisquer outros dois vetores u′u' e v′v' para os quais ‖u′‖2=‖v′‖2\left\|u'\right\|_2 = \left\|v'\right\|_2 e u′-v′u'-v' está na mesma direção que u-vu-v, teremos v′=Qu′v' = Qu'. A matriz QQ reflete o vetor u′u' através do plano perpendicular à u-vu-v e que passa pela origem e pelo ponto médio u+v2\frac{u+v}{2}. Portanto, QQ representa uma transformação linear, denominada transformação de Householder.


Voltar ao Topo.

Fatoração QR utilizando Transformações de Householder

Nesta seção veremos como podemos utilizar as transformações de Householder para o cálculo dos fatores QQ e RR de uma matriz AA.

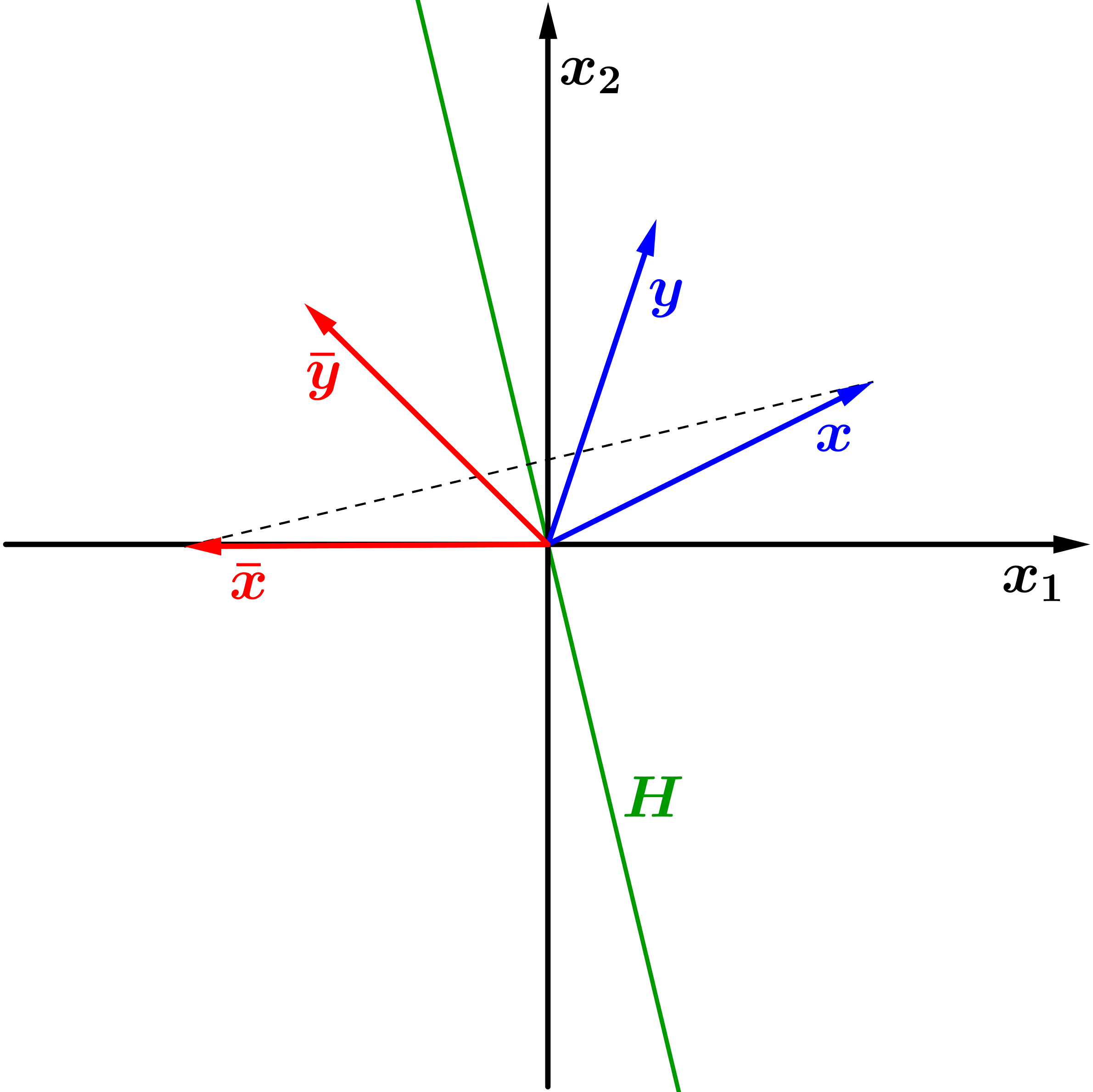
Seja x=(x1,x2,...,xn)tx = (x_1, x_2, ..., x_n)^t um vetor do RnR^n que é levado em um vetor x¯\bar{x} pela transformação. Se x1≥0x_1 \geq 0 definimos x¯=(-‖x‖2,0,...,0)t\bar{x} = \left(-\left\|x\right\|_2, 0, ..., 0 \right)^t e se x1<0x_1 < 0 definimos x¯=(‖x‖2,0,...,0)t\bar{x} = \left(\left\|x\right\|_2, 0, ..., 0 \right)^t. O motivo de definirmos desta forma o vetor após a transformação é numérico e ficará evidente a seguir, pois queremos evitar uma possível subtração entre números próximos. Considere o segmento que une xx com x¯\bar{x}, e o hiperplano HH ortogonal à este segmento e que passa pelo seu ponto médio (x+x¯)2\frac{(x+\bar{x})}{2}, conforme a Figura 3:
ex3_householder
Figura 3: Interpretação geométrica da reflexão de vetores do R2R^2 através do hiperplano HH.

Definição: Denominamos a transformação de Householder definida por x a transformação linear TT que leva um elemento y∊Rny \in R^n à sua reflexão T(y)=y¯T(y) = \bar{y} em relação ao hiperplano HH. Se v=x-x¯v = x - \bar{x}, então:

y¯=y-2vvtvtvy⇒y¯=(In-2vvtvtv)y\bar{y} = y - \frac{2vv^t}{v^tv}y \Rightarrow \bar{y} = \left(I_n - \frac{2vv^t}{v^tv}\right)y
onde
Q=In-2vvtvtvQ = I_n - \frac{2vv^t}{v^tv}
é a matriz da transformação de Householder definida por xx.

A matriz de Householder é simétrica e ortogonal. De fato, temos:

Qt=(In-2vvtvtv)t=Int-(2vvtvtv)t=In-2(vt)tvtvtv=In-2vvtvtv=QQ^t = \left( I_n - \frac{2vv^t}{v^tv} \right)^t = I_n^t - \left( \frac{2vv^t}{v^tv} \right)^t = I_n - \frac{2(v^t)^tv^t}{v^tv} = I_n - \frac{2vv^t}{v^tv} = Q
E então,
QQT=(In-2vvtvtv)(In-2vvtvtv)=In-4vvtvtv+4v(vtv)vt(vtv)2=In-4vvtvtv+4vvtvtv=InQQ^T = \left(I_n - \frac{2vv^t}{v^tv} \right) \left(I_n - \frac{2vv^t}{v^tv} \right) = I_n - \frac{4vv^t}{v^tv} + \frac{4v(v^tv)v^t}{(v^tv)^2} = I_n - \frac{4vv^t}{v^tv} + \frac{4vv^t}{v^tv} = I_n


Uma sequência de transformações de Householder pode ser usada para triangularizar uma matriz. Considere a seguinte matriz:

A=[a11a12⋯a1na21a22⋯a2n⋮⋮⋱⋮an1an2⋯ann]A = \left[ \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{array}\right]
Seja H1=Q1H_1 = Q_1 a matriz da transformação de Householder definida pelo vetor coluna (a11,a21,...,an1)t(a_{11}, a_{21}, ..., a_{n1})^t. Então:

Q1A=[r11r12⋯r1n0a22(1)⋯a2n(1)⋮⋮⋱⋮0an2(1)⋯ann(1)]Q_1A = \left[ \begin{array}{cccc} r_{11} & r_{12} & \cdots & r_{1n} \\ 0 & a^{(1)}_{22} & \cdots & a^{(1)}_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ 0 & a^{(1)}_{n2} & \cdots & a^{(1)}_{nn} \end{array}\right]
Agora, seja H2H_2 a matriz da transformação de Householder definida por (a22(1),...,an2(1))t\left(a^{(1)}_{22}, ..., a^{(1)}_{n2}\right)^t. Queremos multiplicar a matriz Q1AQ_1A por um fator que altere a submatriz A(1)A^{(1)}, mas sem alterar as entradas obtidas na primeira linha e primeira coluna de Q1AQ_1A. Para isto, consideramos a matriz em blocos:

Q2=[100H2]Q_2 = \left[ \begin{array}{cc} 1 & 0 \\ 0 & H_2 \end{array}\right]
Então:

Q2(Q1A)=[r11r12r13⋯r1n0r22r23⋯r2n00a23(2)⋯a2n(2)⋮⋮⋮⋱⋮00an3(2)⋯ann(2)]Q_2(Q_1A) = \left[ \begin{array}{ccccc} r_{11} & r_{12} & r_{13} & \cdots & r_{1n} \\ 0 & r_{22} & r_{23} & \cdots & r_{2n} \\ 0 & 0 & a^{(2)}_{23} & \cdots & a^{(2)}_{2n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & a^{(2)}_{n3} & \cdots & a^{(2)}_{nn} \end{array}\right]
Continuamos com este processo até triangularizar a matriz AA, obtendo uma matriz RR triangular superior. Sendo HkH_k a matriz de Householder obtida na etapa k, teremos:

Qk=[Ik-100Hk]Q_k = \left[ \begin{array}{cc} I_{k-1} & 0 \\ 0 & H_k \end{array}\right]
Após n-1n-1 etapas, obtemos:

(Qn-1...Q2Q1)A=R(Q_{n-1}...Q_2Q_1)A = R
Chamando Qt=Qn-1...Q2Q1Q^t = Q_{n-1}...Q_2Q_1 e como todas as matrizes Q1,Q2,...,Qn-1Q_1, Q_2, ..., Q_{n-1} são ortogonais e o produto de matrizes ortogonais é uma matriz ortogonal, temos:

QtA=R⇔A=QRQ^tA = R \Leftrightarrow A = QR
onde QQ é ortogonal e RR é triangular superior. Assim, obtemos a fatoração ortogonal da matriz AA.


Exemplo 1: Considere a seguinte matriz:

A=[110011101]A = \left[\begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \end{array}\right]
Vamos encontrar a fatoração QRQR de AA utilizando transformações de Householder. Seja u1=(1,0,1)tu_1 = (1, 0, 1)^t. Como a coordenada x1=1≥0x_1 = 1 \geq 0, definimos u1¯=(-‖u1‖2,0,0)t=(-2,0,0)t\bar{u_1} = (-\left\|u_1\right\|_2, 0, 0)^t = (-\sqrt{2}, 0, 0)^t. Seja:

v1=u1-u1¯=(1+2,0,1)tv_1 = u_1 - \bar{u_1} = (1+\sqrt{2}, 0, 1)^t
A matriz da transformação de Householder definida por u1u_1 é dada por:

H1=Q1=I3-2v1v1tv1tv1=[100010001]-24+22[3+2201+20001+201]=H_1 = Q_1 = I_3 - \frac{2v_1v_1^t}{v_1^tv_1} = \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] - \frac{2}{4 + 2\sqrt{2}}\left[\begin{array}{ccc} 3+2\sqrt{2} & 0 & 1+\sqrt{2} \\ 0 & 0 & 0 \\ 1+\sqrt{2} & 0 & 1 \end{array}\right] =
=[100010001]-2-22[3+2201+20001+201]=[100010001]-12[2+202000202-2]⇒= \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] - \frac{2 - \sqrt{2}}{2}\left[\begin{array}{ccc} 3+2\sqrt{2} & 0 & 1+\sqrt{2} \\ 0 & 0 & 0 \\ 1+\sqrt{2} & 0 & 1 \end{array}\right] = \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] - \frac{1}{2}\left[\begin{array}{ccc} 2+\sqrt{2} & 0 & \sqrt{2} \\ 0 & 0 & 0 \\ \sqrt{2} & 0 & 2-\sqrt{2} \end{array}\right] \Rightarrow
⇒Q1=-12[2020-2020-2]\Rightarrow Q_1 = -\frac{1}{2}\left[\begin{array}{crr} \sqrt{2} & 0 & \sqrt{2} \\ 0 & -2 & 0 \\ \sqrt{2} & 0 & -\sqrt{2} \end{array}\right]
Assim, temos que:

Q1A=-12[2020-2020-2][110011101]=-12[22220-2-202-2]Q_1A = -\frac{1}{2}\left[\begin{array}{crr} \sqrt{2} & 0 & \sqrt{2} \\ 0 & -2 & 0 \\ \sqrt{2} & 0 & -\sqrt{2} \end{array}\right]\; \left[\begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \end{array}\right] = -\frac{1}{2}\left[\begin{array}{crr} 2\sqrt{2} & \sqrt{2} & \sqrt{2} \\ 0 & -2 & -2 \\ 0 & \sqrt{2} & -\sqrt{2} \end{array}\right]
Agora, seja u2=(1,-22)tu_2 = \left(1, -\frac{\sqrt{2}}{2}\right)^t. Como x1=1≥0x_1 = 1 \geq 0, definimos u2¯=(-‖u2‖2,0)t=(-32,0)t\bar{u_2} = \left(-\left\|u_2\right\|_2, 0\right)^t = \left(-\frac{\sqrt{3}}{\sqrt{2}}, 0\right)^t.  Seja:

v2=u2-u2¯=(2-32,-22)t=12(2-3,-1)tv_2 = u_2 - \bar{u_2} = \left(\frac{\sqrt{2}-\sqrt{3}}{\sqrt{2}}, -\frac{\sqrt{2}}{2}\right)^t =\frac{1}{\sqrt{2}} \left(\sqrt{2}-\sqrt{3}, -1\right)^t
A matriz da transformação de Householder definida por u2u_2 é dada por:

H2=I2-2v2v2tv2tv2=[1001]-13-6[5-263-23-21]=H_2 = I_2 - \frac{2v_2v_2^t}{v_2^tv_2} = \left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right] - \frac{1}{3-\sqrt{6}}\left[\begin{array}{cc} 5-2\sqrt{6} & \sqrt{3}-\sqrt{2} \\ \sqrt{3}-\sqrt{2} & 1 \end{array}\right] =
=[1001]-3+63[5-263-23-21]=[1001]-13[3-6333+6]⇒= \left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right] - \frac{3+\sqrt{6}}{3}\left[\begin{array}{cc} 5-2\sqrt{6} & \sqrt{3}-\sqrt{2} \\ \sqrt{3}-\sqrt{2} & 1 \end{array}\right] = \left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right] - \frac{1}{3}\left[\begin{array}{cc} 3-\sqrt{6} & \sqrt{3} \\ \sqrt{3} & 3+\sqrt{6} \end{array}\right] \Rightarrow
⇒H2=-13[-6336]\Rightarrow H_2 = -\frac{1}{3}\left[\begin{array}{rc} -\sqrt{6} & \sqrt{3} \\ \sqrt{3} & \sqrt{6} \end{array}\right]
Queremos obter uma matriz Q2Q_2 que triangularize a matriz Q1AQ_1A, sem alterar suas entradas na primeira linha e primeira coluna. Assim, consideramos:

Q2=[100H2]=-13[-3000-63036]Q_2 = \left[\begin{array}{rc} 1 & 0 \\ 0 & H_2 \end{array}\right] = -\frac{1}{3}\left[\begin{array}{rrr} -3 & 0 & 0 \\ 0 & -\sqrt{6} & \sqrt{3} \\ 0 & \sqrt{3} & \sqrt{6} \end{array}\right]
Então:

Q2(Q1A)=16[-3000-63036][22220-2-202-2]=16[-62-32-32036600-43]Q_2(Q_1A) = \frac{1}{6}\left[\begin{array}{rrr} -3 & 0 & 0 \\ 0 & -\sqrt{6} & \sqrt{3} \\ 0 & \sqrt{3} & \sqrt{6} \end{array}\right] \;\left[\begin{array}{crr} 2\sqrt{2} & \sqrt{2} & \sqrt{2} \\ 0 & -2 & -2 \\ 0 & \sqrt{2} & -\sqrt{2} \end{array}\right] = \frac{1}{6}\left[\begin{array}{rrr} -6\sqrt{2} & -3\sqrt{2} & -3\sqrt{2} \\ 0 & 3\sqrt{6} & \sqrt{6} \\ 0 & 0 & -4\sqrt{3} \end{array}\right]
Chamando Qt=Q2Q1Q^t = Q_2Q_1, temos:

Qt=16[-3000-63036][2020-2020-2]=16[-320-32626-623-23-23]⇔Q^t = \frac{1}{6}\left[\begin{array}{rrr} -3 & 0 & 0 \\ 0 & -\sqrt{6} & \sqrt{3} \\ 0 & \sqrt{3} & \sqrt{6} \end{array}\right]\; \left[\begin{array}{rrr} \sqrt{2} & 0 & \sqrt{2} \\ 0 & -2 & 0 \\ \sqrt{2} & 0 & -\sqrt{2} \end{array}\right] = \frac{1}{6}\left[\begin{array}{rrr} -3\sqrt{2} & 0 & -3\sqrt{2} \\ \sqrt{6} & 2\sqrt{6} & -\sqrt{6} \\ 2\sqrt{3} & -2\sqrt{3} & -2\sqrt{3} \end{array}\right] \Leftrightarrow
⇔Q=16[-32623026-23-32-6-23]\Leftrightarrow Q = \frac{1}{6}\left[\begin{array}{rrr} -3\sqrt{2} & \sqrt{6} & 2\sqrt{3} \\ 0 & 2\sqrt{6} & -2\sqrt{3} \\ -3\sqrt{2} & -\sqrt{6} & -2\sqrt{3} \end{array}\right]
Portanto, obtemos os fatores:

Q=16[-32623026-23-32-6-23];R=16[-62-32-32036600-43]Q = \frac{1}{6}\left[\begin{array}{rrr} -3\sqrt{2} & \sqrt{6} & 2\sqrt{3} \\ 0 & 2\sqrt{6} & -2\sqrt{3} \\ -3\sqrt{2} & -\sqrt{6} & -2\sqrt{3} \end{array}\right]; \;\;\;\;\;\;\;\;\;\; R = \frac{1}{6}\left[\begin{array}{rrr} -6\sqrt{2} & -3\sqrt{2} & -3\sqrt{2} \\ 0 & 3\sqrt{6} & \sqrt{6} \\ 0 & 0 & -4\sqrt{3} \end{array}\right]
com QQ ortogonal, pois é produto de matrizes ortogonais e RR triangular superior, tais que A=QRA = QR.


Voltar ao Topo.
Última Atualização: 02/02/2016.