Topologia   Algébrica

Exercícios

1. Mostrar que $\mathbb{C} P^1\simeq S^2$.
   Solução

2. Mostrar que o plano projetivo é homeomorfo ao cone sobre o mapa $f:S^1\subset \mathbb{C}\rightarrow S^1\subset \mathbb{C}$ definido por $f(z)=z^2$.
   Solução

3. Considere $p: S^n\rightarrow \mathbb{R} P^n$ para $n>1$ a projeção canónica. Seja $f:I\rightarrow \mathbb{R} P^n$ definido por \[ f(t)=[(\cos(\pi t),\sin (\pi t),0)] \]
   a) Achar $\pi_1(\mathbb{R} P^2)$
   b) Mostrar que $f$ é um caminho fechado e que $f\star f\simeq [N]$.
   Solução

4. Mostrar que
   a) $C(S^n)\simeq D^{n+1}$ e portanto é um espaço contrátil.
   b) Se $f:S^1\rightarrow S^1$ com $grau(f)\neq\{1,-1\}$ então $C_f=C(S^1)\cup_f S^1$ não é um espaço contrátil.
   Solução

5. Seja $(\tilde Y,q)$ e $(\tilde X,p)$ espaços de recobrimento de $X$. Se existe uma aplicação contínua $h:\tilde Y\rightarrow \tilde X$ tal que $ph=q$, então $h$ é sobrejetora.
   Solução

6. Mostrar que todo mapa do plano projetivo em si mesmo que é não trivial no grupo fundamental pode ser levantado a um mapa $T:S^2\rightarrow S^2$ tal que $T(-x)=-T(x)$ para todo $x\in S^2$.
   Solução

7. Sejam \[ S^1=\{z\in \mathbb{C},~|z|=1\},\quad D=\{z\in \mathbb{C},~|z|\leq 1\},\]\[ S^2=\{(z,x)\in \mathbb{C}\times \mathbb{R},~|z|^2+x^2=1\}, \] quais dos seguintes mapas são de recobrimento? \begin{eqnarray*} p_1:S^1\rightarrow S^1&&p_1(z)=z^4\\ p_2:D\backslash \{0\}\rightarrow S^1&&p_2(z)=\frac{z}{|z|}\\ p_3:S^2\rightarrow D&&p_3(z,x)=z \end{eqnarray*}
   Solução

8. Seja $p:\tilde X\rightarrow X$ um mapa de recobrimento, com $X$ localmente conexo por caminhos, e $Z$ um espaço topológico conexo. Em qual dos seguintes casos podemos concluir que $g=h$?
   a) Se $g:Z\rightarrow \tilde X$ e $h:Z\rightarrow \tilde X$ são mapas contínuos tais que $p\circ g=p\circ h$ e $g(z_0)=h(z_0)$ para algum $z_0\in Z$.
   b) Se $p_*\pi_1(\tilde X,\tilde x_0)=\pi_1(X,x_0)$ e $g:Z\rightarrow \tilde X$ e $h:Z\rightarrow \tilde X$ homeomorfismos contínuos tais que $p\circ g=p\circ h$.
   Solução

9. 
   -Mostre que para $n\geq 2$ temos que $\mathbb{R} P^{n}\simeq \mathbb{R} P^{n-1}\cup e^n$ para $e^n$ uma $n-$célula.
   -Utilizando o teorema de Van-Kampen determine $\pi_1(\mathbb{R} P^n)$ para $n\geq 1$
   Solução

10. Determine $\textbf{Cov}(\tilde X/X)$ para os seguintes espaços de recobrimento
    - $p:\mathbb{R}\rightarrow S^1$ com $p(x)=e^{2\pi i x}$
    - $p_1:\tilde X_1\rightarrow S^1\vee S^1$
    - $p_2:\tilde X_2\rightarrow S^1\vee S^1$.
                  
    Em cada caso dê um exemplo de transformação de recobrimento.
    Solução

11. Determine para quais valores de $n\in \{2,3,4\}$ a seguinte afirmação é sempre verdadeira: "Se $f:SO(n)\rightarrow T^n$ contínuo então $f$ é homotópico ao mapa constante"
    Solução

12. Podemos anexar uma 3-célula à garrafa de Klein e obter um espaço contrátil? Caso a resposta seja afirmativa, indique como deve ser o mapa anexante $\phi|_{S^2}$.
    Solução

13. Calcule $\pi_1(\mathbb{C} P^n).$
    Solução

14. Seja $X$ um espaço topológico e defina a suspensão de $X$ como sendo o espaço $\sum X=X\times I/\sim$ onde $(x,1)\sim P$ e $(x,0)\sim Q$. Mostrar que
    i- $\tilde H_q(X)=\tilde H_{q+1}(\sum X).$
    ii- $\sum S^n\simeq S^{n+1}$.
    iii- $H_n(S^n)=H_1(S^1)$.
    Solução

15. Calcular os seguintes grupos de homologia
    i- $H_n(K)$ para $K$ sendo a garrafa de Klein.
    ii- $H_n(\mathbb{C} P^2$ #$\mathbb{C} P^2)$
    iii-$ H_2(\mathbb{C} P^1\times S^3)$.
    Solução

16. 
    i- Assuma que existe a fibração $S^k\cdots S^{n+k}\rightarrow S^n$. Mostrar que $k=n-1.$
    ii- Calcular $\pi_i(\mathbb{C} P^n)$ para $1\leq i\leq 2n+1$.
    Solução

17. Se $p:X\rightarrow Y$ é um mapa de recobrimento com $X$ simplesmente conexo então $\pi_1(Y)$ age nas fibras de duas formas
    1) Por transformações de Deck
    2) Por monodromia.
    Mostrar que estas duas ações conicidem se, e somente se, $\pi_1(Y)$ é abeliano.
    Solução

18. 
    i- Seja $F\cdots E\rightarrow^p B $ uma fibração e assuma que admite uma seção, isto é, existe um mapa contínuo $\sigma:B\rightarrow E $ tal que $p\circ\sigma=I_B$. Mostrar que $\pi_n(E)\simeq \pi_n(F)\oplus\pi_n(B)$ para $n\geq 2.$
    ii- Calcule $H_n(S^n\times S^m) $ para $m>n.$
    Solução

19. Calcule a homologia dos seguintes espaços
    a) O espaço $X$ obtido de anexar um disco $D^2$ na parte superior da calça pelo mapa $\phi:S^1\rightarrow S^1$ dado por $\phi(z)=z^2$
    b) $H_n(SO(3))$ para $n\geq 0$.
    c) $H_n(\mathbb{C} P^1\vee \mathbb{R} P^2)$ para $n\geq 0$.
    Solução

20. Calcule
    a) $\pi_2(\mathbb{C} P^1\vee S^3)$.
    b) $\pi_3(\mathbb{C} P^3\times \mathbb{C} P^1)$.
    Solução

21. Sejam $p:E\rightarrow B$ e $q:B\rightarrow B'$ fibrações, então $q\circ p:E\rightarrow B'$ fibração.
    Solução

22. Seja $M$ o quociente de $I\times D^2$ obtido ao identificar \[(0,z)\sim (1,\bar{z}),\] onde $D^2\subset \mathbb{C}$. Denote a fronteira (uma garrafa de Klein ) deste espaço por $K$. Ache $\pi_2(M,K).$
    Solução

23. Se $\pi_4(S^3)=\mathbb{Z} _2$ o que podemos dizer de $\pi_5(S^4\times S^5)$?
    Solução

24. Considere, para $n\geq 2$, a ação de $\mathbb{Z} \times \mathbb{R}^{n(n-1)/2}\rightarrow \mathbb{R}^{n(n-1)/2}$ definida por \[k\cdot (x_1,x_2,\ldots,x_{n(n-1)/2})=(x_1+k,x_2,\ldots,x_{n(n-1)/2}) \] e seja $X_n$ o espaço quociente associado a essa ação. Para quais valores de $n$ podemos garantir que qualquer mapa $f:SO(n)\rightarrow X_n$ é homotópicamente nulo?
    Solução

25. Seja $Y\subset X$ subespaço topológico de um espaço conexo por caminhos. Defina \[Z=\big(Y\times [0,1])\sqcup X\big)/\sim\] onde \[(y_1,0)\sim (y_2,0)\quad\forall y_1,~y_2\in Y\quad\textrm{e}\quad (y,1)\sim y\in X\quad \forall y\in Y.\] Compare (são isomorfas?, uma pode ser vista como subgrupo da outra? ou não há relação entre elas) as homologias $H_n(X,Y)$ e $H_n(Z)$.
    Solução

26. Sejam $U,~V$ abertos de um espaço $X$. Compare (são isomorfas?, uma pode ser vista como subgrupo da outra? ou não há relação entre elas) \[H_k(U, U\cap V)\quad \textrm{e}\quad H_k(U\cup V,V).\]
    Solução

27. 
    i- Mostrar que se $f:S^n\rightarrow S^n$ é um mapa contínuo que não é uma equivalência homotópica, então $f$ possui um ponto fixo.
    ii- Mostrar que toda função contínua de $g:\mathbb{R} P^2\rightarrow \mathbb{R} P^2$ tem um ponto fixo.
    Solução

28. 
    i- $H_*(\mathbb{R} P^2;\mathbb{R})$,
    ii- $H_*(S^4\times S^2,\mathbb{Z}_4)$
    iii- $H_*(K,\mathbb{Z}_2)$ para $K$ a garrafa de Klein.
    Solução

29. Construa um espaço $X$ que possua a mesma Homologia que $T^2=S^1\times S^1$ e que não seja homeomorfo a $T^2$.
    Solução

30. Sejam $X,~Y$ complexos CW finitos, conexos, de dimensão $n$ e com exatamente uma $n$-célula.
    i- Mostre que $H_n(X)$ é zero ou isomorfo a $\mathbb{Z}$,
    ii- Mostre que se $H_n(X)\simeq\mathbb{Z}$ ent\~ao $H_{n-1}(X)\simeq H_{n-1}(X^{n-1})$ onde $X^{n-1}$ é o $n-1$ esqueleto de $X$.
    iii- Mostre que se $H_n(X)\simeq\mathbb{Z}\simeq H_n(Y)$ então \[H_k(X\sharp Y)= \left\{\begin{array}{ccl} H_k(X)\oplus H_k(Y)&se&k=1\ldots n-1\\\mathbb{Z}&se&k=0,~n\\ 0&&c.c. \end{array} \right. \]
    Solução

31. Mostre que $S^1\vee S^2\vee S^3$ e $S^1\times S^2$ não tem o mesmo tipo de homotopia.
    Solução

32. 
    i- Mostrar que se $f:S^n\rightarrow S^n$ é um mapa contínuo que não é uma equivalência homotópica, então $f$ possui um ponto fixo.
    ii- Mostrar que toda função contínua de $g:\mathbb{R} P^2\rightarrow \mathbb{R} P^2$ tem um ponto fixo.
    Solução

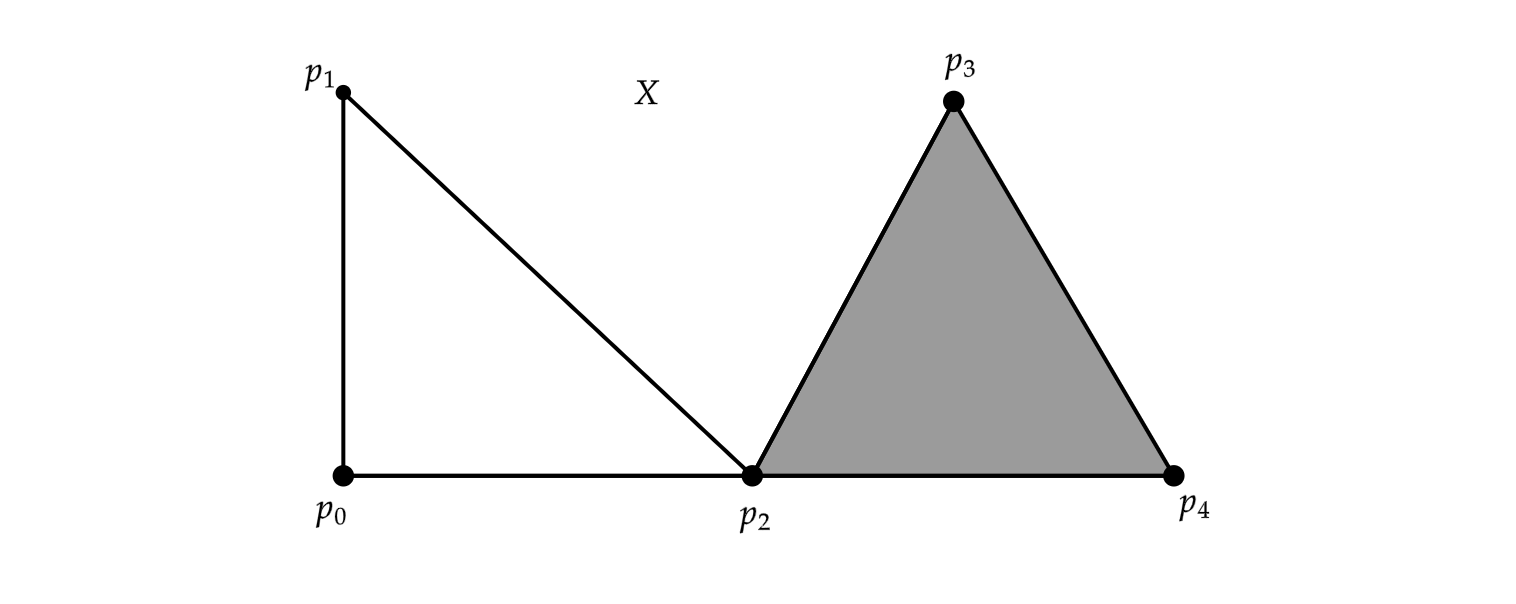
33. Calcule a Homologia simplicial do complexo simplicial associado ao espaço $X$ visto como subespaço de $\mathbb{R}^2$.
    
    Solução

34. Considere, para $n\geq 2$ o meridiano $S^{n-1}\subset S^n$. Seja \[\nu:S^n\rightarrow S^n/S^{n-1}\simeq S^n\vee S^n\] a aplicação ao quociente. Assumimos, sem perder generalidade, que o ponto união de $S^n\vee S^n$ é o polo norte $\{N\}\subset S^n$. Considere agora $f,~g:S^n\rightarrow S^n$ dois mapas tais que $g(N)=f(N)$ e defina $f\vee g:S^n_1\vee S^n_2\rightarrow S^n$ \[ f\vee g(x)=\left\{\begin{array}{ccc}f(x)&\textrm{se}&x\in S^n_1\\g(x)&\textrm{se}&x\in S^n_2\end{array}\right. \] Calcule o grau do mapa $(f\vee g)\circ \nu:S^n\rightarrow S^n$ em termos de $grau(f)$ e $grau(g)$.
    Solução

35. Considere $f:S^n\rightarrow S^n$ um mapa contínuo e considere $\Sigma f:\Sigma S^n\rightarrow \Sigma S^n$. Calcule o número de Lefchetz de $\Sigma f$ em função do número de Lefchetz de $f$.
    É possível concluir que, para $n\in\mathbb{N}$ e $k\in\mathbb{Z}$ podemos achar um $f:S^n\rightarrow S^n$ tal que o seu número de Lefchetz seja igual a $k$?.
    Solução

36. Considere o espaço $X$ dado como no desenho abaixo.
    
    para $\phi_i:S^1\rightarrow S^1$ dados por $\phi_i(z)=z^{k_i}$ para $k_i\in\mathbb{Z}$.
    i- Dé uma estrutura de CW complexo para $X$.
    ii- Constrúa o complexo celular e calcule, utilizando o item anterior, a homologia CW de $X$.
    Solução

37. Constrúa um espaço $X$ que tenha a mesma homologia que $Y=T^2\vee S^2$ mas que não seja homotópicamente equivalente a este. Faça as contas utilizando homologia CW ou celular.
    Solução

38. Calcule o anel de cohomologia de $X=\mathbb{C} P^n\times \mathbb{C} P^m$ com coeficientes em $\mathbb{Z}$. Discuta sobre a existência de um mapa $\phi:\mathbb{C} P^{n+m}\rightarrow X$ tal que $\phi_*:H_2(\mathbb{C} P^{n+m})\rightarrow H_2(X)$ é não trivial.
    Solução

39. Seja $f:\mathbb{R}^2\rightarrow \mathbb{R}^2$ o mapa $f(x,y)=(-x-y,x)$. Como este é um mapa linear e preserva a lattice de $\mathbb{Z}^2$, induz um mapa $f:T^2\rightarrow T^2$ no toro. Seja $w_0\in T^2$ o ponto correspondente à origem de $\mathbb{R}^2$.
    a) Encontre $f_*:\pi_1(T^2,w_0)\rightarrow \pi_1(T^2,w_0)$ e utilize isto para achar $f_*:H_1(T^2)\rightarrow H_1(T^2)$
    b) Encontre $f_*:H_2(T^2)\rightarrow H_2(T^2)$
    c) Mostre que um mapa $g:T^2\rightarrow T^2$ homotópico a $f$ tem um ponto fixo.
    Solução

40. Seja $Y$ o espaço resultante de $D^3$ ao identificar os pontos em $S^2$ pela rotação em 180 gaus ao redor do eixo vertical. Dê uma decomposição CW do espaço e calcule sua Homologia.
    Solução

41. 
    Solução