Princípio de Fermat |
PARTE I |
|
|
Na Óptica Geométrica vale o Princípio de Fermat: A trajetória do raio que liga dois pontos é aquele que minimiza o tempo de percurso. O problema que vamos explorar é encontrar o(s) ponto(s) no espelho onde ocorre(m) a reflexão de um raio. Para este problema, ainda vale o Princípio de Fermat, só que, neste caso, há a inclusão de um vínculo. Matematicamente falando, o problema pode ser descrito como: procuramos os pontos estacionários do seguinte problema de minimização:
Minimizar T(x,y),
O primeiro algoritmo básico para achar o(s) ponto(s) do espelho onde
há reflexão é:
A abordagem correspondente ao primeiro algoritmo é:
quando possível, isolar y na restrição y = f(x), substituir em T(x,y), gerando uma nova função de uma variãvel t=t(x)=T(x,f(x)), e, finalmente, achar os pontos críticos dessa nova função t(x). Em seguida vamos aplicar o algoritmo em três exemplos. |
||
Reflexão em espelho plano |
exemplo I.1 |
|

|
||
|
Figura I.1 Exemplo do Algoritmo I sendo usado para a determinação do ponto de reflexão (M), do raio que sai da fonte (S), reflete no espelho e chega no receptor (G). O espelho é plano horizontal. Siga este link para visualizar o gif animado ou clique aqui para visualizar a animação |
||
Explicação:
|
||
Reflexão em espelho plano inclinado |
exemplo I.2 |
|

|
||
|
Figura I.2 Exemplo do Algoritmo I sendo usado para a determinação do ponto de reflexão (M), do raio que sai da fonte (S), reflete no espelho e chega no receptor (G). O espelho é um plano inclinado. Siga este link para visualizar o gif animado ou clique aqui para visualizar a animação |
||
Observações:
|
||
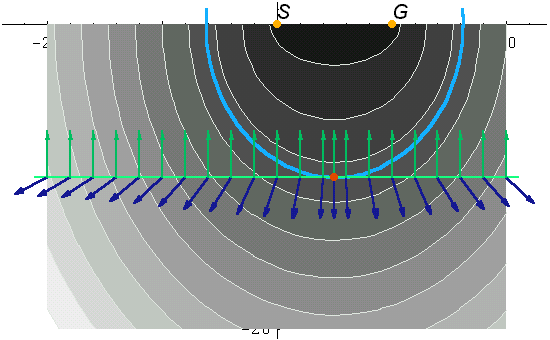
Reflexão em espelho qualquer |
exemplo I.3 |
|
|
||
|
Figura I.3 Exemplo do Algoritmo I sendo usado para a determinação do ponto de reflexão (M), do raio que sai da fonte (S), reflete no espelho e chega no receptor (G). O espelho é não linear. Siga este link para visualizar o gif animado ou clique aqui para visualizar a animação |
||
Observações:
|
||
Multiplicadores de Lagrange |
PARTE II |
|
|
Outra forma de se resolver o problema é utilizar o Teorema dos
Multiplicadores de Lagrange, que diz:
Nos problemas de minimização
Minimizar T(x,y), a grad(T) + b grad(h) =0 Isto é, nos pontos estacionários, o gradiente da função que se deseja minimar e o gradiente da restrição são linearmente dependentes. Isto equivale dizer que os gradientes são colineares nos pontos estacionários. Como os gradientes são ortogonais às curvas de nível, a equação acima se traduz em dizer que as curvas de nível se tangenciam nos pontos estacionários.
Baseado nos resultados do teorema, pode-se considerar um novo
algoritmo:
|
||
Reflexão em espelho plano |
exemplo II.1 |
|
|
Figura II.1 Exemplo do Algoritmo II sendo usado para a determinação do ponto de reflexão (M), do raio que sai da fonte (S), reflete no espelho e chega no receptor (G). O espelho é plano horizontal. Siga este link para visualizar o gif animado ou clique aqui para visualizar a animação |
||
Reflexão em espelho plano inclinado |
exemplo II.2 |
|

| ||
|
Figura II.2 Exemplo do Algoritmo II sendo usado para a determinação do ponto de reflexão (M), do raio que sai da fonte (S), reflete no espelho e chega no receptor (G). O espelho é um plano inclinado. Siga este link para visualizar o gif animado ou clique aqui para visualizar a animação |
||
Reflexão em espelho qualquer |
exemplo II.3 |
|

| ||
|
Figura II.3 Exemplo do Algoritmo II sendo usado para a determinação do ponto de reflexão (M), do raio que sai da fonte (S), reflete no espelho e chega no receptor (G). O espelho é não linear. Siga este link para visualizar o gif animado ou clique aqui para visualizar a animação |
||
Multiplicadores de Lagrange |
PARTE III |
|
|
Existe ainda uma terceiro modo de se determinar os pontos de reflexao usando o Teorema dos Multiplicadores de Lagrange. Sabemos que nos pontos estacionarios do problema, a equaçãão deve ser satisfeita a grad(T) + b grad(h) =0 Portanto, podemos procurar, ao longo do refletor h(x)=0, pontos que satisfazem a equação acima. Essa ideia da origem ao nosso terceiro algoritmoAlgoritmo III
|
||
Reflexão em espelho plano |
exemplo III.1 |
|
|
Figura III.1 Exemplo do Algoritmo III sendo usado para a determinação do ponto de reflexão (M), do raio que sai da fonte (S), reflete no espelho e chega no receptor (G). O espelho é plano horizontal. Siga este link para visualizar o gif animado ou clique aqui para visualizar a animação |
||
Reflexão em espelho plano inclinado |
exemplo III.2 |
|

|
||
|
Figura III.2 Exemplo do Algoritmo III sendo usado para a determinação do ponto de reflexão (M), do raio que sai da fonte (S), reflete no espelho e chega no receptor (G). O espelho é um plano inclinado. Siga este link para visualizar o gif animado ou clique aqui para visualizar a animação |
||
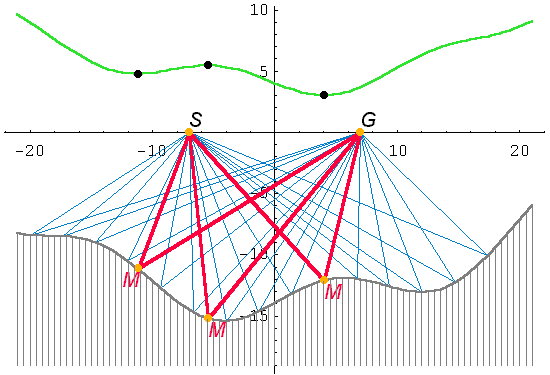
Reflexão em espelho qualquer |
exemplo III.3 |
|

|
||
|
Figura III.3 Exemplo do Algoritmo III sendo usado para a determinação do ponto de reflexão (M), do raio que sai da fonte (S), reflete no espelho e chega no receptor (G). O espelho é não linear. Siga este link para visualizar o gif animado ou clique aqui para visualizar a animação |
||