Tente resolver os três exercícios propostos abaixo, marque as respostas nas caixas de texto correspondentes e depois clique nos botões para verificar se as respostas estão corretas.

1 - Um pedreiro gasta 12 horas para erguer um muro de 3 metros de altura e 4 metros de comprimento.

a) Quanto tempo o mesmo pedreiro levaria para erguer um muro de 3 metros de altura e 8 de comprimento?
R: horas

b) Quanto tempo ele levaria para erguer um muro de 3 metros de altura e 2 de comprimento?
R: horas

c) E para erguer um muro de 3 metros de altura e 20 de comprimento?
R: horas



2 - Seu avô, quando viajou para a praia, levou 4 horas para chegara até Santos. Durante a viagem, a velocidade do carro foi de 60 km/h.

a)Quanto tempo ele levaria se viajasse a 120 km/h?
R: horas

b)Quanto tempo ele levaria se viajasse a 30 km/h?
R: horas

c)E se ele fosse bem devagar, por exemplo a 15 km/h, quanto tempo levaria?
R: horas



3 - Para fazer um bolo, sua mãe usa 3 copos de trigo, 2 ovos, 2 copos de leite e 4 colheres de açucar.

a)Quantos ovos ela gastaria para fazer 3 receitas? E quantos copos de trigo?
R: ovos e copos de trigo.

b)Para fazer meia receita, quantas colheres de açucar ele gastaria? E quantos copos de leite?
R: colheres de açucar e copos de leite.

c)Se sua mãe tem apenas 8 copos de trigo, quantas receitas inteiras ela pode fazer?
R: receitas


Veja que, sabendo apenas o tempo que o pedreiro gasta para construir um muro de 3 metros de altura por 4 de comprimento, você é capaz de descobrir quanto tempo ele vai levar pra construir um muro com outras medidas. Sabendo o tempo que seu avô gastou em uma viagem e a velocidade dele nessa viagem, foi possível descobrir quanto tempo ele gastaria se fosse mais devagar ou mais rápido.

Para explorarmos melhor essa capacidade de "prever" valores, faremos uma série de exercícios, chegaremos a diversas conclusões e usaremos diversos recursos como equações e gráficos. A equação que será usada é extremamente simples, mas alguns de vocês podem não estar familiarizados com a construção e utilização de gráficos, para aprimorar essa capacidade clique aqui.

Além disso, utilizaremos um plotador de pontos várias vezes durante as atividades que seguem, apesar de sua utilização ser bastante simples, você pode encontrar dificuldades ao utilizá-lo. Caso isso realmente aconteça, acesse o link acima e vá direto ao final.

1 - Uma caixa d'água está furada no fundo. Por causa disso, ela perde 2 litro de água a cada 1 hora. Marque no gráfico, considerando o tempo no eixo X e a quantidade de água perdida no eixo Y, as respostas de cada item:

a) Quantos litros de água vazaram da caixa em 2 horas?
b) E em 3 horas?
c) E em 5 horas?
d) E em meia hora?



2 - Em uma feira, cada dúzia de bananas custa R$ 1,20 . Marque no gráfico as respostas dos itens:

a) Quanto custará 2 pencas de banana?
b) E 3 pencas?
c) E 4 pencas?
d) E 6 bananas?

A Equação
No exercício 2 como você faria para calcular o preço de 8 pencas?

Para calcular o preço, basta multiplicar o preço de uma penca pelo número de pencas (8). Ou seja:
Preço total = preço por penca x número de pencas

No primeiro exercício, para calcular a quantidade de água perdida, o procedimento usado é muito parecido:

Quantidade de água perdida total = quantidade de água perdida por hora x número de horas

Observe que nos dois casos a construção é muito parecida. Para generalizar, podemos escrever o seguinte:

Y = K . X

Onde X e Y assumem significados diferentes para cada exercício e K é chamada de constante de proporcionalidade.

PROPORCIONALIDADE DIRETA

Dizemos que duas grandezas X e Y são proporcionais quando podemos escrever a relação entre elas na forma Y=K.X, onde Y e X são chamadas de variáveis (pois os valores que assumem variam) e K é chamada constante (pois assume um único valor).

Como calcular a constante K

Como dito, em toda relação de proporcionalidade, o valor de k é o mesmo independentemente dos valores que você escolheu para X e Y.
O valor dessa constante é fundamental quando estudamos grandezas proporcionais, veja como podemos calculá-la:

Y = K.X
se dividirmos os dois lados por X, temos:
Y / X = K

Ou seja, podemos calcular o valor de K dividindo um valor de Y por um de X. Fazendo isso, também podemos testar se uma relação é proporcional ou não. Se dividirmos dois valores de Y por dois de X e os valores obtidos forem diferentes, podemos concluir que a relação entre essas grandezas não é proporcional. Acompanhe esse exemplo:

Exemplo 1

Numa tarde chuvosa em São paulo, foi montada a seguinte tabela que relaciona o número de horas com chuva e o aumento do nível do rio Tietê em centímetros.

Aumento no nível do rioTempo com chuva
28 cm.2 hora
42 cm.3 hora
56 cm.4 hora
a) Verifique se a relação é de proporcionalidade direta.

Chamemos o tempo de chuva de X e o aumento no nível de água do rio de Y. Se dividirmos os valores da primeira coluna (Y) da tabela pelos valores da segunda (X) teremos o seguinte:
28 / 2 = 14
42 / 3 = 14
56 / 4 = 14
Logo, temos sim uma relação de proporcionalidade direta!

 b) Calcule o valor de K para essa relação.

Sabemos que K = Y / X, mas já calculamos isso no item anterior, ou seja, K = 14. Isto signfica que, a cada hora de chuva o nível do rio sobe 14 cm, e por isto, para medir o aumento do nível do rio, como função do tempo de chuva, adotamos a unidade de medida cm/hora.

c) Quanto o nível do rio havia subido na quinta hora de chuva?

Temos que Y = K . X, substituindo os valores:
Y = 14 . 5
Y = 70
Portanto, o nível do rio subiu 70 centímetros nas cinco primeiras horas de chuva.
d) Neste dia, como é comum acontecer no verão, a chuva começou no começo da tarde, às 14 horas, quando o leito do rio se encontrava 126 cm abaixo do nível das pistas marginais. Às 19 horas, os técnicoas da Companhia de Engenharia de Trânsito conversaram entre sí prevendo que, se a chuva continuasse neste ritmo, às 21 horas, eles anunciaram o estado de alerta contra enchentes. Qual é o nível do rio que determina o estado de alerta contra enchentes?

Se a chuva começou às 14 horas e neste ritmo o estado de alerta seria decretado às 21 horas, temos que este seria decretado após 7 horas de chuva. Assim como antes, temos que, para X = 7 obtemos:
Y = 14 . 7
Y = 98
Como às 14 horas a água do rio estava 126 cm abaixo do nível da pista, temos que no momento de decretar o estado de alerta, a água estaria a 126 - 98 = 28 cm abaixo da pista. Ou seja, o estado de alerta é decretado quando o nível do rio é inferior a 28 centimetros em relação às pistas.

Exemplo 2

A tabela abaixo mostra a área de um quadrado e o valor do seu lado.

Área (cm2)Medida do lado (cm)
4 cm22 cm
9 cm23 cm
25 cm25 cm

a) Qual a área do quadrado de lado 4 cm?

A área do quadrado é dada por A = lado x lado, logo, se o lado vale 4:
A = 4 x 4
A = 16 cm2

b) A área e a medida do lado de um quadrado são proporcionais?

Para isso, vamos dividir a área do quadrado pela medida do seu lado para obter K e verificar se esse valor é constante:
4 / 2 = 2
9 / 3 = 3
25 / 5 = 5
Nos bastava que apenas um dos valores de K fosse diferente para concluirmos que a relação não é proporcional!

c) Agora, utilize o plotador abaixo e marque os pontos calculados nesse exercício. O que você pode dizer sobre o formato desse gráfico em relação aos gráficos das relações proporconais que você estudou?





Exemplo 3

Um motoboy cobra, por viagem, 6 reais pelo serviço mais 1,20 reais por minuto viajado. Pergunta-se:

a) Quanto custa uma viagem que dura 2 minutos? E uma de 3 minutos?

Traduzindo o enunciado do exercício para uma fórmula: Preço = (6 + 1,20 x tempo)
Para facilitar a escrita, vamos chamar o tempo de T e o preço de P, logo: P = 6 + (1,20 x T)
Calculando o que se pediu:

P = 6 + (1,20 x 2), P = 7,20
P = 6 + (1,20 x 3), P = 8,40

Note que nesse exemplo estamos denotando nossas variáveis pelas letras P (para preço) e T (para tempo de viagem), ao invés das letras X e Y utilizadas anteriormente. Na realidade nada mudou, apenas o símbolo utilizado.

b) Calcule o preço de viagens mais longas ou curtas e marque os pontos no plotador.



Observe que se calcularmos razão P/T para dois pares de valores calculados em a), veremos que eles são diferentes:

Se T=2, então P=7,20 e Y/X=7,20/2= 3,60
Se T=3, então P=8,40 e Y/X=8,40/3= 2,80

Portanto, não se trata de uma relação de proporcionalidade.

c) Compare os gráficos proporcionais que você já fez com o gráfico acima. O que eles tem de comum e de diferente?


Esse fato nos leva a uma conclusão importante, você já deve ter percebido que sempre que se trata de uma relação proporcional, o gráfico é uma reta. No entanto, nem toda reta é gráfico de uma relação proporcional pois, se Y=K.X, temos que quando X=0 também temos Y=0, ou seja, a reta deve passar pela origem (ponto (0;0)).

Portanto, temos duas maneiras de distinguir relações de proporção das demais relações, uma é analisando o gráfico, a outra é verificando através dos dados disponíveis se existe uma constante de proporcionalidade.

Exemplo

Escreva sim ou não nas caixas de texto correspondentes aos gráficos que são ou não de uma relação proporcional.

1 2
3 4
5



conforme vimos, a relação de proporcionalidade é muito freqüente. No entanto, inúmeros fenômenos naturais e sociais importantes, não respeitam a relação de proporcionalidade. Clique aqui para conhecer alguns exemplos adicionais, ou então vá direto à lista de exercícios abaixo.

1- O gráfico abaixo representa o consumo de álcool (Y) de um carro em função da distância percorrida (X). Utilizando o gráfico calcule o que se pede:



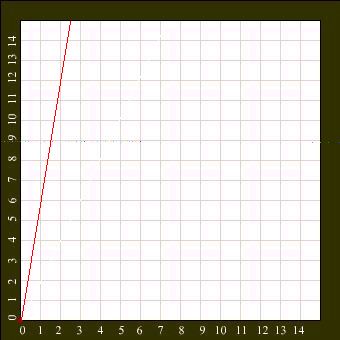
a) o valor de K (leia no gráfico um valor e calcule com ele o valor K)

R:

b) a quantidade de álcool consumida para se percorre 6 kilômetros.
R: litros

c) o consumo para uma distância de 9 kilômetros.
R: litros

d) a distância máxima percorrida por um automóvel com 12 litros de álccol no tanque
R: quilômetros



2- Uma barra de metal dilata-se proporcionalmente ao aumento de temperatura que sofre, ou seja, esta encolhe quando a temperatura diminui e aumenta junto com a temperatura. A constante de proporcionalidade K dessa relação é chamada de coeficiente de dilatação. Sabendo que o coeficiente de dilatação de uma barra de alumínio de 1 metro de comprimento é 0,025 mm/ºC, responda:

a) Se a temperatura da barra aumentar 4ºC, em quantos centímetros esta aumentará?
R: milímetros

b) Quando se constrói ferrovias ou metrôs, são utilizadas barras de alumínio de aproximadamente 1 metro de comprimento para montar os trilhos. Se as barras forem colocadas uma encostada na outra e a temperatura aumentar pode ocorrer uma deformação nos trilhos que pode acarretar um acidente. Um engenheiro ao construir um novo trecho de metrô em São Paulo descobre que a maior variação de temperatura no local é de 40ºC. Qual a distância mínima que ele deve deixar entre cada barra de alumínio para que não ocorra deformação nos trilhos devido à variação de temperatura?
R: milímetros



3- Em um experimento, um cientista queria determinar o coeficiente de dilatação de uma barra de um metal desconhecido, para isso coletaram valores e mantaram a seguinte tabela:

DilataçãoVariação da Temperatura
0,034 mm2ªC
0,068 mm4ªC
0,102 mm6ªC

a) Qual o coeficiente de dilatação desse metal?
R:

b) Depois de realizar a experiência, o cientista esqueceu a barra do metal no sol e ela esquentou 5ºC. Quanto o metal deveria dilatar?
R:

c) Quando se descobriu que cada metal possui seu próprio coeficiente de dilatação e percebeu-se que seu cálculo era muito simples, criaram-se tabelas que enumeravam diferentes metais e seus respectivos coeficientes de dilatação. Segue abaixo um trecho dessa tabela (que é muito longa para ser copiada inteira). Baseando-se nela e no valor que você encontrou no item a, responda: qual o metal em questão?

MaterialCoeficiente de dilatação
Alumínio0,025
Prata0,019
Cobre0,017
Ferro0,009
Zinco0,026
Ouro0,014

R:



Faça você mesmo!
clique aqui para acessar uma experiência que você mesmo pode fazer em casa.

Inclinação

Você já deve ter observado que os gráficos de funções proporcionais são lineares, e essas retas possuem uma inclinação diferente. Nessa seção iremos estudar a inclinação das retas dos gráficos de funções lineares.
Para começar, vamos analisar os três gráficos abaixo, que ilustram o preço do tomate em três cidades do Brasil: o primeiro gráfico se refere a compra na cidade São Paulo, o segundo em Goiânia e o terceiro em Natal. Todos se referem a mesma relação: o preço em reais (no eixo Y) em relação ao peso em quilogramas (no eixo X).


a) nalisando estes gráficos, determine o preço de um quilo de tomate em cada uma destas cidades.
b) Com auxílio de um transferidor, meça o ângulo que cada gráfico faz com o eixo X (horizontal) e compare estes com as constantes de proporcionalidade. Qual a relação entre estes ângulos e as constantes de proporcionalidade?



Como você deve ter observado, quanto maior o valor de K em uma relação de proporcionalidade, maior o ângulo de inclinação da reta.
Essa relação sempre se verifica em qualquer proporcionalidade direta e é muito importante para uma análise primária de um gráfico. Por exemplo, se você vir dois gráficos de preço de algum produto ou serviço de diferentes empresas, você já será capaz de saber qual é mais caro sem precisar calcular os valores, basta verificar qual está mais inclinado!

Uma última observação

Analisemos o seguinte exemplo:

Uma relação de proporcionalidade é regida pela seguinte fórmula: Y = 3.X.

a) Escolha um valor de X, calcule o valor de Y para esse valor escolhido e anote-os nas caixas de texto abaixo.
R:

b) Qual o valor de Y se dobrarmos o valor escolhido para X?
R:

c) Qual o valor de Y se triplicarmos o valor escolhido para X
R:



d) O que aconteceu com o valor de Y quando dobramos o valor de X? E quando triplicamos?



e) Volte e verifique para, pelo menos, um caso de relação proporcional que você já resolveu se essa relação verifica também vale. O que você verificou?



Ou seja, para qualquer relação de proporcionalidade vale essa propriedade de que quando dobramos (isto é, multiplicamos por 2) o valor de X, o mesmo ocorre com Y, quando triplicamos (isto é, multiplicamos por 3) o valor de X, o mesmo ocorre com Y... generalizando, quando multiplicamos o valor de X por um número qualquer, o valor resultante para Y também é multiplicado pelo mesmo número.

Agora, faça os exercícios abaixo para testar os últimos conceitos aprendidos.
1- A constante de proporcionalidade que rege a relação entre o espaço percorrido por um corpo e o tempo transcorrido é chamada de velocidade. Quanto maior a velocidade de um móvel, você deve saber disso, mais espaço ele percorre (mais longe ele vai) em menos tempo. Os gráficos abaixo representam a posição (Y) de dois carros diferentes em função do tempo (X) em minutos. Analisando os dois gráficos abaixo, responda:

Carro 1 Carro 2

a) Qual a posição do carro 1 aos 5 minutos?
R: kilômetros

b) E do carro 1 aos 5 minutos?
R: kilômetros

c) Quem é mais rápido?
R: (1 ou 2)

c) Qual a constante K do mais rápido? (essa constante representa a velocidade em kilômetros por minuto)
R: km/min



c) Marque alguns pontos a sua escolha equivalentes ao consumo do carro do meu tio e do meu pai, respectivamente, no primeiro e no segundo plotador, compare a inclinação da reta formada pelos pontos nos dois e anote sua conclusão na caixa de texto abaixo.

2- Um fio de cabelo cresce em média 0,8 cm/ano. Responda:

a) Quantos centímetros o cabelo de Márcia crescerá em dois anos?
R: cm

b) Quantos centímetros crescerá em 4 anos
R: cm

b) Se Carlos raspou o cabelo no começo do ano e pretende ficar com 3 cm de comprimento, quantos meses ele deve esperar?
R: cm


Fechar