The SCORE of a structural alignment
The quality of the alignment between two structures is evaluated by measures that are usually called scores. Scores must take into account two properties of a structural alignment: 1) The number of atoms in the correspondence and, 2) the quality of the superposition between corresponding atoms.For example, the frequently used Root-Mean-Square-Deviation (RMSD), is not a valid score by itself: two proteins may share a very similar core, but differ in a mobile loop or hinge. The superposition of the mobile loop and hinge will result in a large value for the RMSD between the two structures, and we will not be able to recognize the similarity of the cores.
Because of this, several scores have been proposed that are able, using a single value, indicate the quality of the alignment. In LovoAlign we have implemented three of them, which we believe are the most relevant. Each has its particular properties that may be of interest in specific cases:
1 - TM-Score
The TM-Score was proposed by Zhang and Skolnick [ref]. This score was weighted according the size of the structures being compared and by the study of the quality of general alignments, in such a way that it varies between 0 and 1, from a bad to a good superposition. It was shown that scores below 0.17 indicate that the superposition is not better than the superposition of two random structures. Because of the quality of this score as an absolute measure of the quality of protein alignments, it is recommended as the default choice for the comparison of two protein structures.
2 - Structal score
The Structal score was proposed by Levitt and co-workers [ref]. It has a similar structure than the TM-Score, but it is parametrized as:
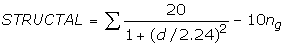
3 - Triangular score
The Triangular score is very simple. It is maximal when the position of corresponding atoms coincide, and decreases linearly to zero for a distance defined by the user (the default value in LovoAlign being 3.0 Angstroms). This score, therefore, can be used for the identification of common cores in protein structures, as it will totally neglect the substructures that are poorly aligned. Furthermore, by using this score one is able to personally and intuitively determine what one considers as a good alignment. For instance, one can state that only atoms which are closer than 2 Angstroms should be considered. The optimization of this score will find the best superposition of the structures that maximizes the number of atoms that can be aligned within that tolerance. It can be demonstrated, furthermore [ref], that the RMSD found for these atoms is the best one for the given correspondence, in such a way that the RMSD obtained using this score, for the corresponding atoms, is meaningful. For the other score, one could similarly compute the RMSD of the atoms which are within a desired tolerance, but the alignment of these atoms would not be the perfect one, and could be improved by an additional rigid-body alignment. The optimization of the Triangular score automatically satisfies this requirement. Furthermore, the Triangular score for non-bijective alignments can be computed very rapidly [ref], and this can be important for database comparisons.