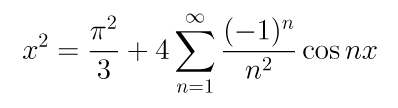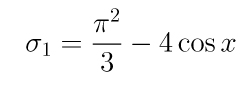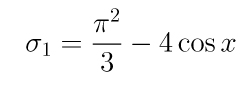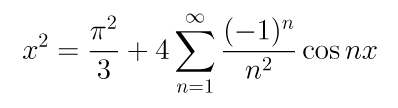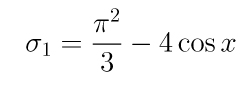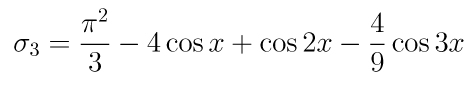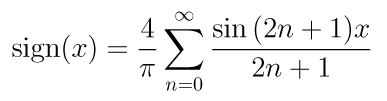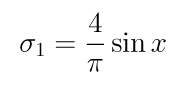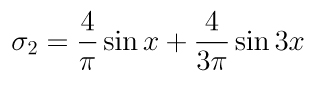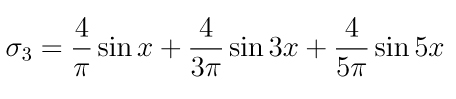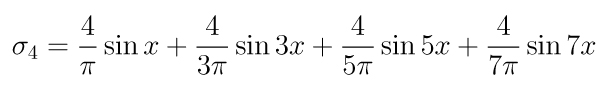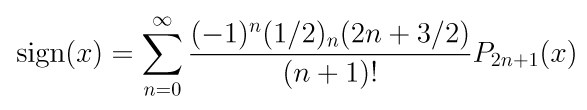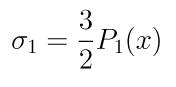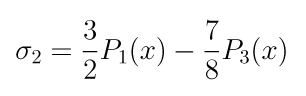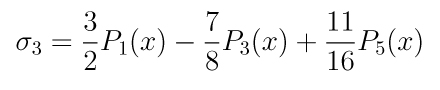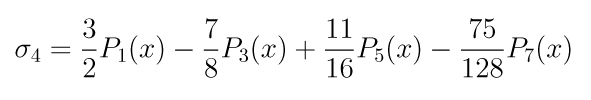Como no caso anterior, temos uma representação da
função sign(x) no intervalo (-Pi,Pi), enquanto em toda
reta temos uma representação da extensão
periódica da função restrita ao intervalo
considerado. Evidentemente, o que diferencia um exemplo do outro
é que no
presente caso a função f(x) = sign(x) apresenta uma
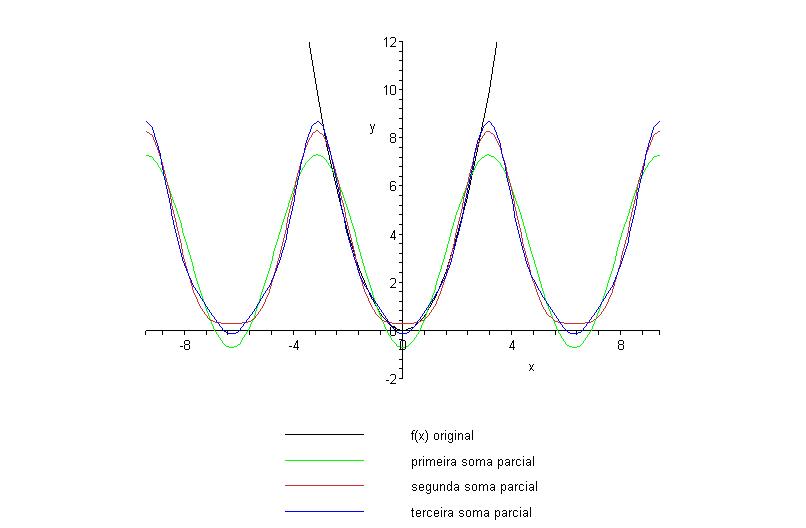
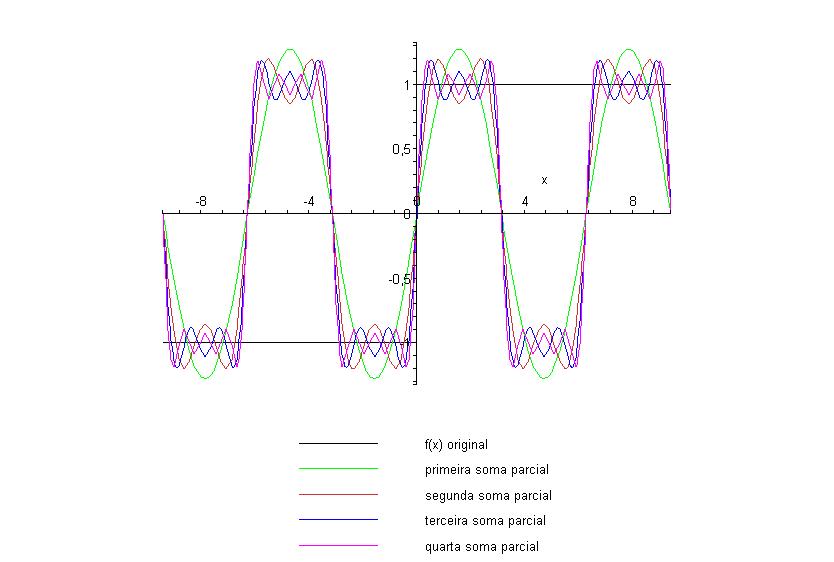
descontinuidade em x = 0. Podemos notar, como afirma o teorema de
Fourier, que a série converge para o valor médio dos
limites laterais. No caso do ponto x = 0, o limite pela esquerda de
f(x) é -1 enquanto o limite pela direita de f(x) é 1, de
modo que o valor médio é 0, que é justamente o
ponto de convergência, como mostram claramente os gráficos
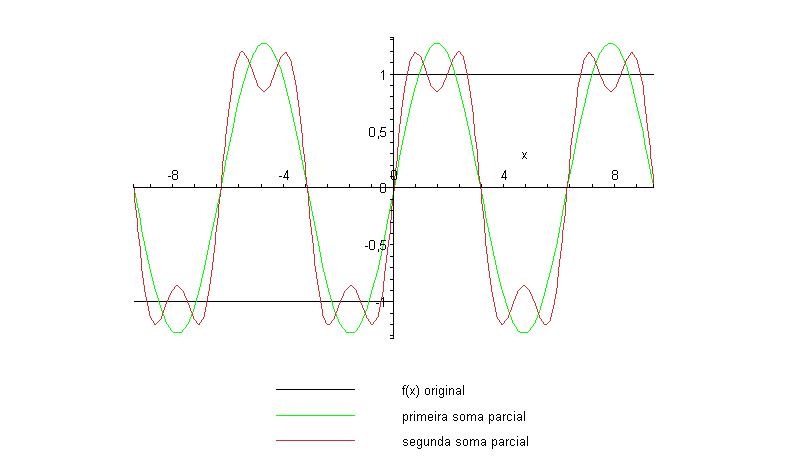
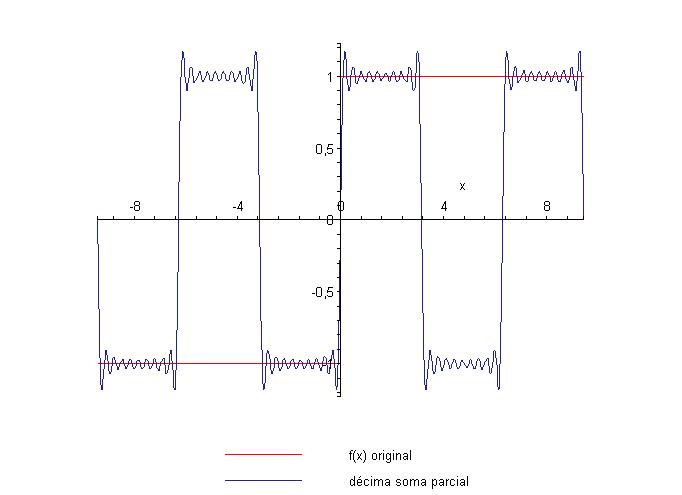
acima. Além disso, podemos notar a presença do
fenômeno de Gibbs, que é o comportamento fortemente
oscilatório das somas parciais à medida que se aproxima o
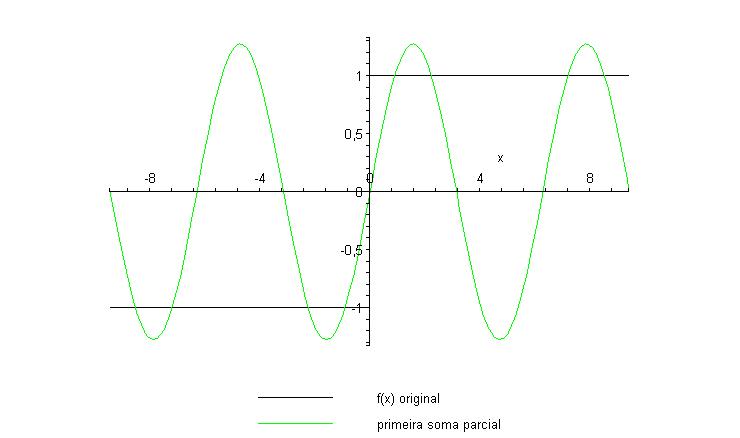
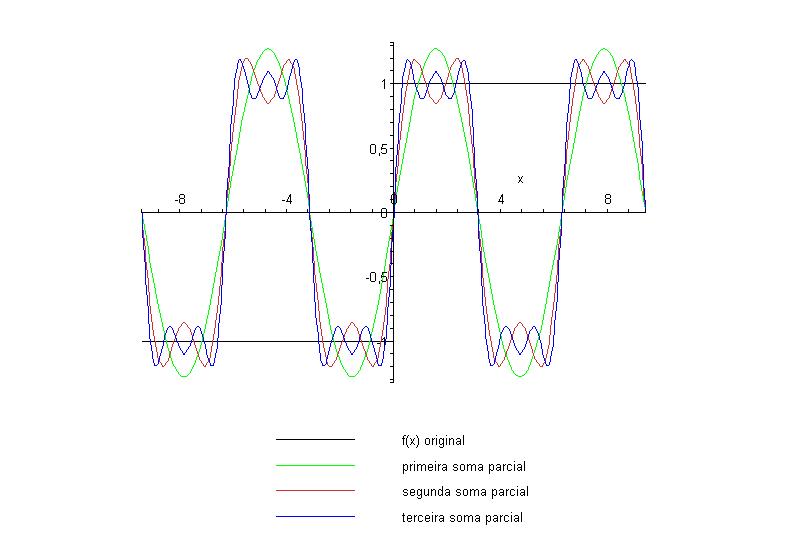
ponto de descontinuidade. Vamos extrair dos gráficos acima a
parte correspondente ao fenômeno de Gibbs:

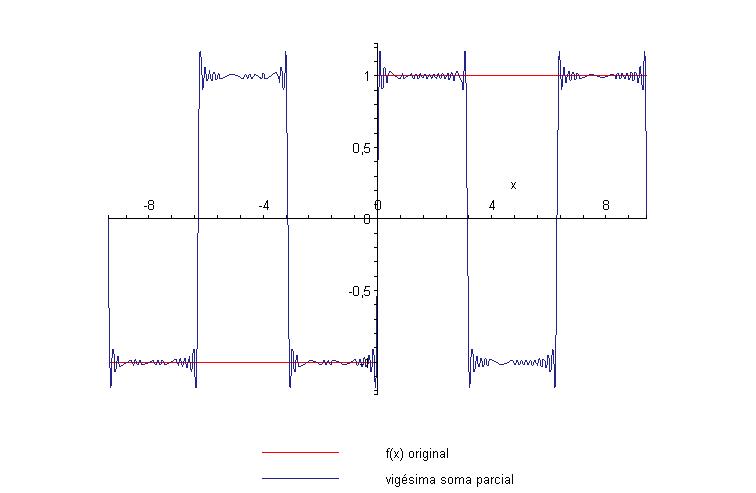
Podemos notar que o ponto de maior (e também o de menor)
amplitude das oscilações se aproxima da descontinuidade
à medida que acrescentamos mais termos às somas parciais.
Entretanto, não é possível eliminar essas
oscilações. Pode-se mostrar que os extremos das
oscilações estão em torno de 18% do valor da
função, ou seja, como nesse caso f(x) = 1 as
oscilações ocorrem (aproximadamente) no intervalo 0,82
< y < 1,18.
As séries de Fourier podem ser generalizadas usando outros
conjuntos de funções além de senos e co-senos.
Podemos também utilizar, dentro de certos intervalos adequados,
funções de Bessel J
n(x), polinômios de
Legendre P
n(x), etc. Por exemplo, a série de
Fourier-Legendre no intervalo (-1,1) da função f(x) =
sign(x) é
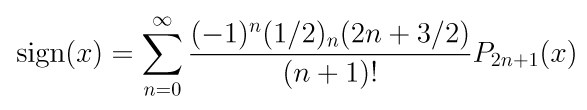
onde (a)
n = a(a+1)...(a+n-1)
é o símbolo de Pochhammer. A primeira soma parcial
é
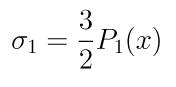
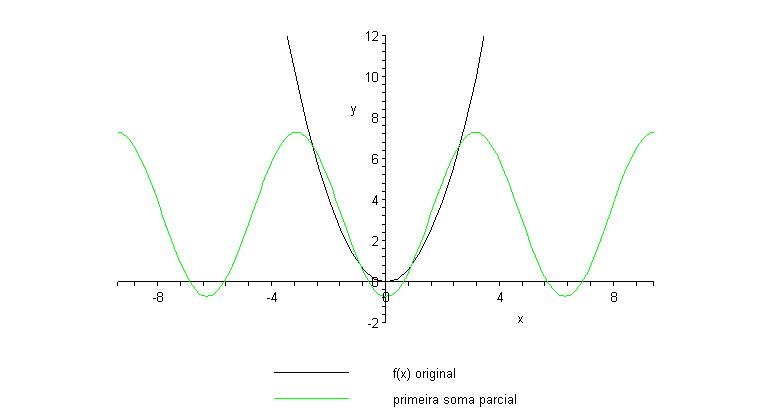
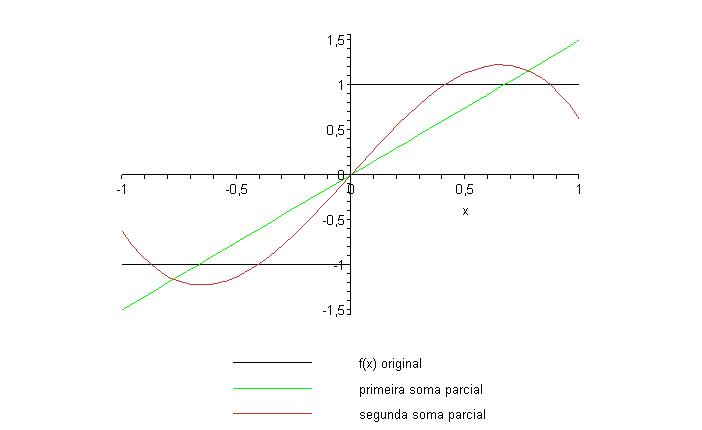
e o gráfico da
função sign(x) e dessa primeira soma parcial é
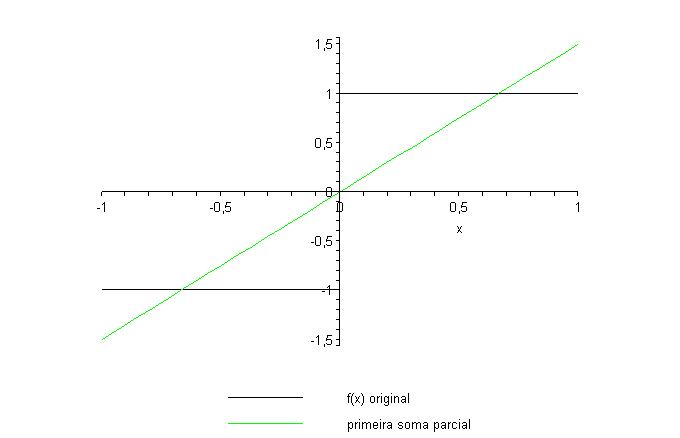
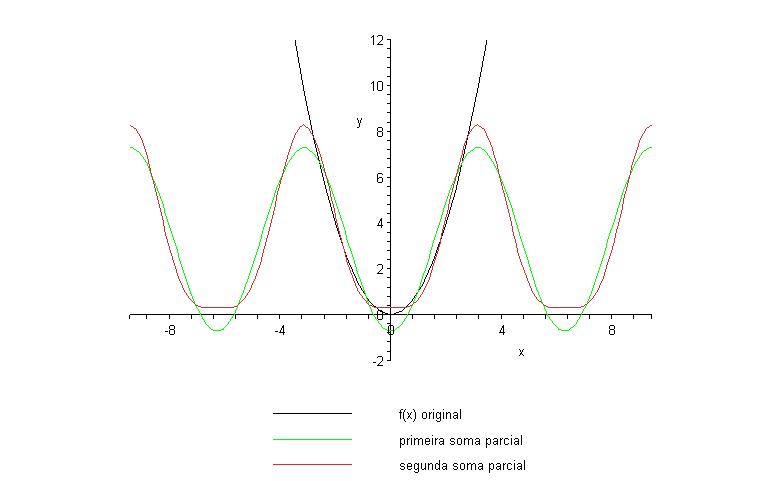
A segunda soma parcial é
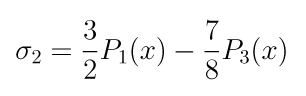
e seu gráfico em conjunto com os
anteriores é
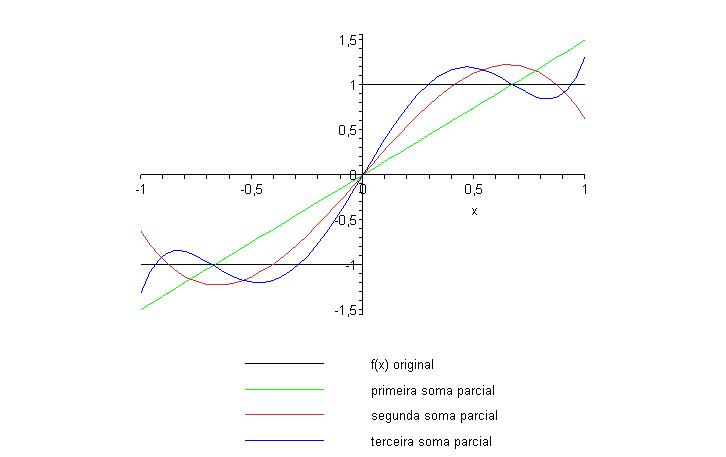
A terceira soma parcial é
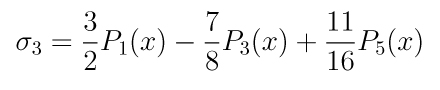
e incluindo esse gráfico na
comparação com os anteriores temos
A quarta soma parcial é
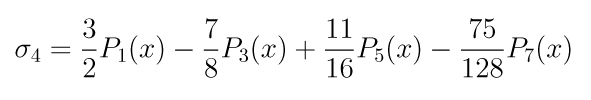
Incluindo mais essa soma parcial na
comparação temos

Podemos notar que o comportamente das somas parciais é
claramente semelhante ao caso anterior, ou seja, independe do fato que
no caso anterior as funções usadas no desenvolvimento da
série serem senos e co-senos e agora serem polinômios de
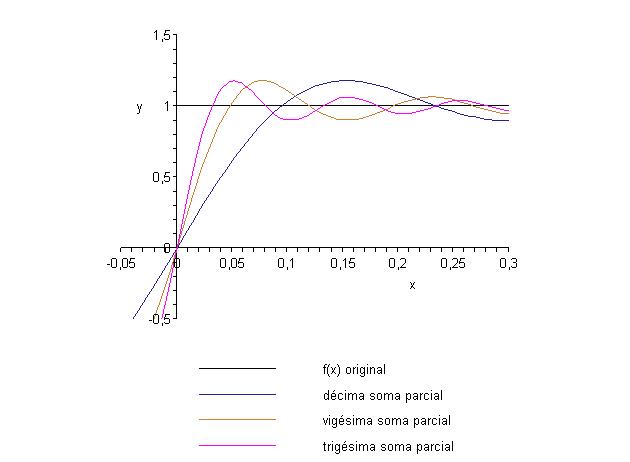
Legendre. O gráfico com a décima soma parcial é
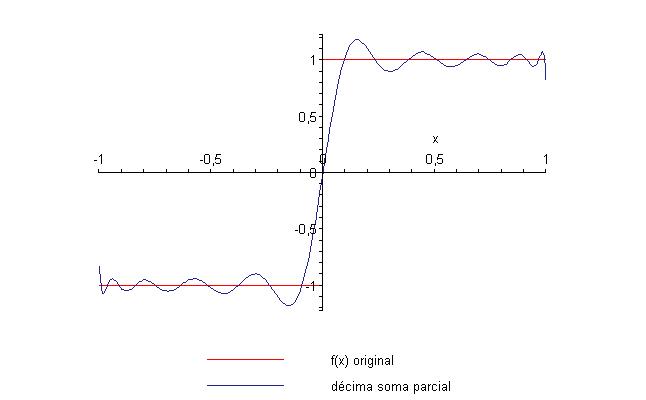
com a vigésima soma parcial é
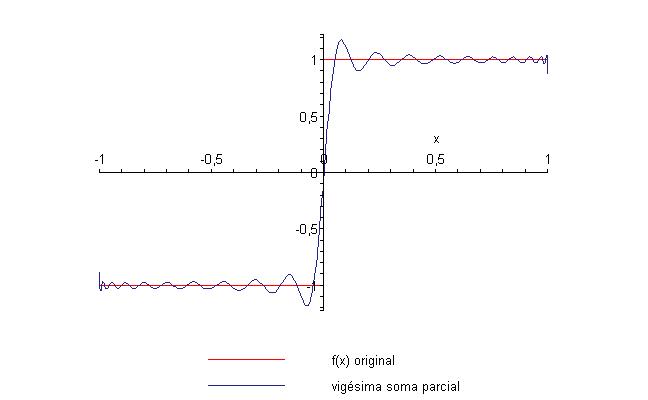
e com a trigésima soma parcial
é
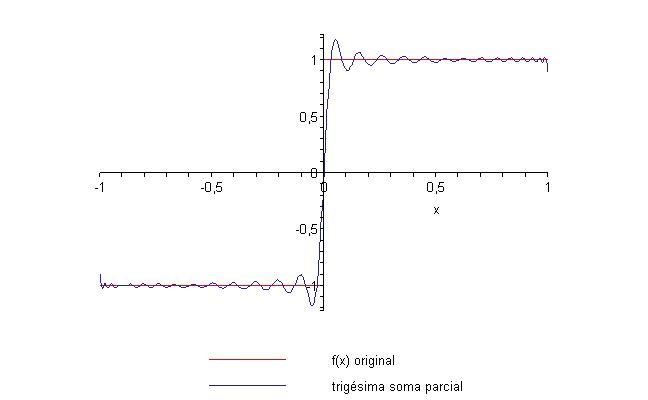
Comparando os gráficos, temos
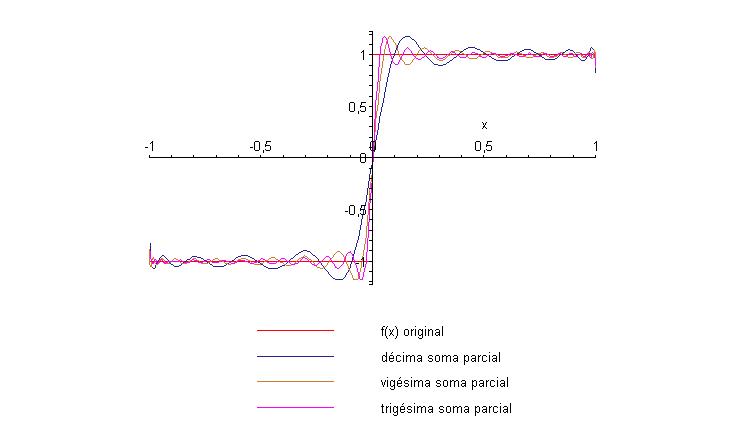
Podemos notar, como esperado, um fênomeno do tipo Gibbs.